Straight Lines Class 11 Questions and Answers - Free PDF Download
FAQs on NCERT Solutions For Class 11 Maths Chapter 9 Straight Lines Exercise 9.1 - 2025-26
1. What is the correct method to find the slope of a line joining two points (x1, y1) and (x2, y2) as per the NCERT solutions for Class 11 Maths Chapter 9?
To find the slope of a line joining two given points, you use the formula: m = (y2 - y1) / (x2 - x1). This formula calculates the change in the y-coordinate (rise) divided by the change in the x-coordinate (run). The result, 'm', represents the steepness of the line. This is a foundational step for solving many problems in the NCERT exercises.
2. How can we use the concept of slopes to prove that three given points are collinear, according to the CBSE 2025-26 syllabus?
To prove that three points, say A, B, and C, are collinear (lie on the same straight line), you need to show that the slope of the line segment AB is equal to the slope of the line segment BC. If slope(AB) = slope(BC), the points are collinear. This method is a key problem-solving technique in NCERT Solutions for Chapter 9.
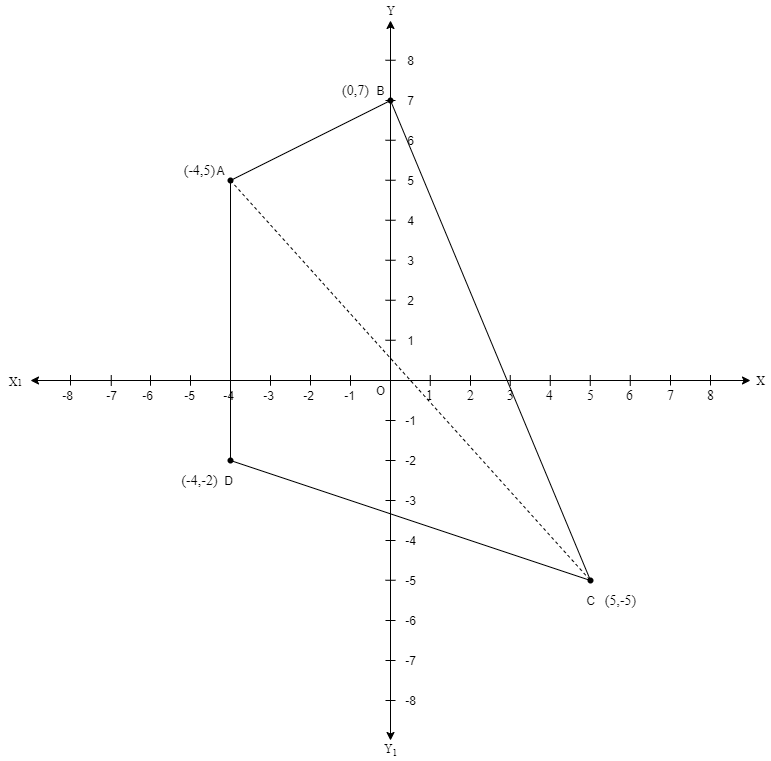
3. What is the step-by-step NCERT method to show that three points form a right-angled triangle without using the distance formula or Pythagoras theorem?
To prove that three points form a right-angled triangle using slopes, follow these steps:
Calculate the slopes of the three lines formed by the points. Let them be m1, m2, and m3.
Check if the product of any two slopes is equal to -1.
If you find that m1 * m2 = -1, it proves that the two lines corresponding to these slopes are perpendicular to each other, thus forming a right angle. This confirms the points are vertices of a right-angled triangle.
4. What are the key forms of the equation of a straight line that students must master for solving NCERT Chapter 9 exercises?
For successfully solving the NCERT exercises for Straight Lines, students must be proficient with the following forms of a line's equation:
Slope-Intercept Form: y = mx + c
Point-Slope Form: y - y1 = m(x - x1)
Two-Point Form: y - y1 = [(y2 - y1)/(x2 - x1)](x - x1)
Intercept Form: x/a + y/b = 1
Normal Form: x cos(ω) + y sin(ω) = p
5. How does the general equation of a line, Ax + By + C = 0, help in solving problems in the NCERT solutions?
The general equation Ax + By + C = 0 is a versatile form used in NCERT solutions to quickly find key properties of a line. From this form, you can directly calculate:
The slope (m) as -A/B.
The x-intercept as -C/A (by setting y=0).
The y-intercept as -C/B (by setting x=0).
6. Why is the slope of a vertical line considered 'undefined' in coordinate geometry, and how does this impact solving NCERT questions?
The slope of a vertical line is considered undefined because for any two points on it, the x-coordinates are the same (x1 = x2). The slope formula m = (y2 - y1) / (x2 - x1) results in division by zero (x2 - x1 = 0), which is mathematically undefined. When solving NCERT problems, if you encounter an undefined slope, you should immediately recognise it as a vertical line with the equation x = k, where k is a constant.
7. What is a common mistake students make when finding the angle between two lines using the formula tan θ = |(m2 - m1) / (1 + m1m2)|?
A common mistake is forgetting the absolute value (modulus) in the formula. The formula calculates the acute angle (θ) between the lines. If you ignore the absolute value, you might get a negative result for tan θ, which would correspond to the obtuse angle. For NCERT problems asking for 'the angle' between two lines, it typically refers to the acute angle, making the modulus crucial for the correct answer.
8. How do you find the distance of a point (x1, y1) from a line Ax + By + C = 0 as per the method in NCERT Chapter 9?
The NCERT-prescribed method to find the perpendicular distance (d) of a point (x1, y1) from the line Ax + By + C = 0 is to use the direct formula: d = |Ax1 + By1 + C| / √(A² + B²). You substitute the coordinates of the point into the line's equation for the numerator and divide by the square root of the sum of the squares of the coefficients of x and y. The absolute value ensures the distance is always positive.
9. Beyond just solving for 'x', why is the concept of collinearity important for understanding the geometry of straight lines?
The concept of collinearity is fundamentally important because it defines the very essence of a straight line—a set of points maintaining a constant slope between any two of them. Understanding this helps in:
Verifying if multiple points belong to the same path.
Serving as a basis for more complex geometric proofs.
Solving problems related to the intersection of lines and geometric figures without complex calculations.
10. Where can I find reliable, step-by-step NCERT Solutions for Class 11 Maths Chapter 9, Straight Lines?
You can find detailed and accurate step-by-step NCERT Solutions for Class 11 Maths Chapter 9 (Straight Lines) on the Vedantu platform. The solutions are prepared by subject matter experts and are aligned with the CBSE 2025-26 syllabus, focusing on providing clear methods to solve all the exercise questions correctly and efficiently for your exams.