Find Complete Trigonometric Functions Class 11 Questions and Answers Here
NCERT Solutions For Class 11 Maths - Trigonometric Functions help you solve angle and triangle problems easily. These functions show how angles connect to sides in triangles. Class 11 students find these topics useful for many math problems.
 Table of Content
Table of ContentKey points covered:
• Solutions for sine, cosine, and tangent function problems
• Step-by-step answers for trigonometric equations and identities
• Practice questions with clear explanations for all exercise problems
• Methods to solve trigonometric function graphs and transformations
Download the NCERT Solutions PDF for free and practice right away! Vedantu's NCERT Solutions make complex trigonometric problems simple to solve. You get detailed steps for every question in the chapter. These solutions save time during exam preparation and homework. Check out NCERT Solutions Class 11 Maths for more chapter-wise help and guidance.
Access Exercise Wise NCERT Solutions for Chapter 3 Maths Class 11
Find Complete Trigonometric Functions Class 11 Questions and Answers Here
Exercise 3.1: In this exercise, students are introduced to trigonometric ratios of acute angles and their applications in solving problems related to heights and distances. The exercise covers basic concepts such as the definition of trigonometric ratios, Pythagoras theorem, and the concept of complementary angles.
Exercise 3.2: This exercise focuses on the evaluation of trigonometric ratios of special angles such as 0, 30, 45, 60, and 90 degrees. The exercise also includes the derivation of trigonometric ratios of 30, 45, and 60 degrees using the concept of the unit circle.
Exercise 3.3: This exercise covers the trigonometric ratios of angles between 0 and 90 degrees. The exercise includes problems on finding the values of trigonometric ratios using various techniques such as the use of Pythagoras theorem, the double-angle formula, and the half-angle formula.
Miscellaneous Exercise: This exercise includes a variety of problems that cover different topics such as the use of trigonometric ratios in solving real-life problems, the use of trigonometric identities to simplify expressions, and the solution of trigonometric equations. This exercise provides an opportunity for students to apply the concepts learned in the chapter to solve more complex problems.
Access NCERT Solution for Class 11 Maths Chapter 3 - Trigonometric Functions
Exercise 3.1
1. Find the radian measures corresponding to the following degree measures:
(i) $\text{2}{{\text{5}}^{\text{o}}}$
Ans: We know that $\text{18}{{\text{0}}^{\text{o}}}\text{= }\!\!\pi\!\!\text{ }$ radian
Therefore ${{1}^{\circ }}=\dfrac{\pi }{180}$ radian
hence,
$\text{2}{{\text{5}}^{\text{o}}}\text{=}\dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{180}}\text{ }\!\!\times\!\!\text{ 25}$ radian
$\text{=}\dfrac{\text{5 }\!\!\pi\!\!\text{ }}{\text{36}}$radian
(ii) $\text{-4}{{\text{7}}^{\text{o}}}\text{30 }\!\!'\!\!\text{ }$
Ans: Here we have,
$\text{-4}{{\text{7}}^{\text{o}}}\text{30 }\!\!'\!\!\text{ =-47}{{\dfrac{\text{1}}{\text{2}}}^{\text{o}}}$
$\text{=-}\dfrac{\text{95}}{\text{2}}$ degree
Since we know that, $\text{18}{{\text{0}}^{\text{o}}}\text{= }\!\!\pi\!\!\text{ }$ radian
Therefore ${{\text{1}}^{\text{o}}}\text{=}\dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{180}}$ radian
Hence,
$\text{-}\dfrac{\text{95}}{\text{2}}$ degree$\text{=}\dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{180}}\text{ }\!\!\times\!\!\text{ }\left( \dfrac{\text{-95}}{\text{2}} \right)$ radian
$\text{=}\left( \dfrac{\text{-19}}{\text{36 }\!\!\times\!\!\text{ 2}} \right)\text{ }\!\!\pi\!\!\text{ }$ radian
$\text{=}\dfrac{\text{-19}}{\text{72}}\text{ }\!\!\pi\!\!\text{ }$radian
Therefore,
$\text{-4}{{\text{7}}^{\text{o}}}\text{30 }\!\!'\!\!\text{ =-}\dfrac{\text{19}}{\text{72}}\text{ }\!\!\pi\!\!\text{ }$ radian
(iii) $\text{24}{{\text{0}}^{\text{o}}}$
Ans: We know that,
$\text{18}{{\text{0}}^{\text{o}}}\text{= }\!\!\pi\!\!\text{ }$ radian
Therefore ${{\text{1}}^{\text{o}}}\text{=}\dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{180}}$ radian
Hence,
$\text{24}{{\text{0}}^{\text{o}}}\text{=}\dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{180}}\text{ }\!\!\times\!\!\text{ 240}$ radian
$\text{=}\dfrac{\text{4}}{\text{3}}\text{ }\!\!\pi\!\!\text{ }$radian
(iv) $\text{52}{{\text{0}}^{\text{o}}}$
Ans: We know that,
$\text{18}{{\text{0}}^{\text{o}}}\text{= }\!\!\pi\!\!\text{ }$ radian
Therefore ${{\text{1}}^{\text{o}}}\text{=}\dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{180}}$ radian
Hence,
$\text{52}{{\text{0}}^{\text{o}}}\text{=}\dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{180}}\text{ }\!\!\times\!\!\text{ 520}$ radian
$\text{=}\dfrac{\text{26 }\!\!\pi\!\!\text{ }}{\text{9}}$radian
2. Find the degree measures corresponding to the following radian measures
(Use$\text{ }\!\!\pi\!\!\text{ =}\dfrac{\text{22}}{\text{7}}$ )
(i) $\dfrac{\text{11}}{\text{16}}$
Ans: We know that,
$\text{ }\!\!\pi\!\!\text{ }$ radian$\text{=18}{{\text{0}}^{\text{o}}}$
Therefore $\text{1 radian =}{{\dfrac{\text{180}}{\text{ }\!\!\pi\!\!\text{ }}}^{\text{o}}}$
Hence,
$\dfrac{\text{11}}{\text{16}}$ radian$\text{=}\dfrac{\text{180}}{\text{ }\!\!\pi\!\!\text{ }}\text{ }\!\!\times\!\!\text{ }\dfrac{\text{11}}{\text{16}}$ degree
$\text{=}\dfrac{\text{45 }\!\!\times\!\!\text{ 11}}{\text{ }\!\!\pi\!\!\text{ }\!\!\times\!\!\text{ 4}}$degree
\[\text{=}\dfrac{\text{45 }\!\!\times\!\!\text{ 11 }\!\!\times\!\!\text{ 7}}{\text{22 }\!\!\times\!\!\text{ 4}}\] degree
$\text{=}\dfrac{\text{315}}{\text{8}}$degree
Further computing,
$\dfrac{\text{11}}{\text{16}}$ radian$\text{=39}\dfrac{\text{3}}{\text{8}}$ degree
$\text{=3}{{\text{9}}^{\text{o}}}\text{+}\dfrac{\text{3 }\!\!\times\!\!\text{ 60}}{\text{8}}$ minutes
Since ${{\text{1}}^{\text{o}}}\text{=60 }\!\!'\!\!\text{ }$
$\dfrac{\text{11}}{\text{16}}$ radian $\text{=3}{{\text{9}}^{\text{o}}}\text{+22 }\!\!'\!\!\text{ +}\dfrac{\text{1}}{\text{2}}$minutes
Since $\text{1 }\!\!'\!\!\text{ =60''}$
$\dfrac{\text{11}}{\text{16}}$ radian$\text{ }\!\!~\!\!\text{ =3}{{\text{9}}^{\text{o}}}\text{22 }\!\!'\!\!\text{ 30''}$
(ii) $\text{-4}$
Ans: We know that,
$\text{ }\!\!\pi\!\!\text{ }$ radian$\text{=18}{{\text{0}}^{\text{o}}}$
Therefore $\text{1 radian =}{{\dfrac{\text{180}}{\text{ }\!\!\pi\!\!\text{ }}}^{\text{o}}}$
Hence,
$\text{-4}$ radian$\text{=}\dfrac{\text{180}}{\text{ }\!\!\pi\!\!\text{ }}\text{ }\!\!\times\!\!\text{ }\left( \text{-4} \right)$ degree
$\text{=}\dfrac{\text{180 }\!\!\times\!\!\text{ 7}\left( \text{-4} \right)}{\text{22}}$degree
$\text{=}\dfrac{\text{-2520}}{\text{11}}$ degree
$\text{=-229}\dfrac{\text{1}}{\text{11}}$degree
Since ${{\text{1}}^{\text{o}}}\text{=60 }\!\!'\!\!\text{ }$
We have,
$\text{-4}$ radian$\text{=-22}{{\text{9}}^{\text{o}}}\text{+}\dfrac{\text{1 }\!\!\times\!\!\text{ 60}}{\text{11}}$ minutes
$\text{=-22}{{\text{9}}^{\text{o}}}\text{+5 }\!\!'\!\!\text{ +}\dfrac{\text{5}}{\text{11}}$ minutes
Since $\text{1 }\!\!'\!\!\text{ =60 }\!\!'\!\!\text{ }\!\!'\!\!\text{ }$
$\text{-4}$ radian$\text{=-22}{{\text{9}}^{\text{o}}}\text{5 }\!\!'\!\!\text{ 27''}$
(iii) $\dfrac{\text{5 }\!\!\pi\!\!\text{ }}{\text{3}}$
Ans: We know that,
$\text{ }\!\!\pi\!\!\text{ }$ radian$\text{=18}{{\text{0}}^{\text{o}}}$
Therefore $\text{1 radian =}{{\dfrac{\text{180}}{\text{ }\!\!\pi\!\!\text{ }}}^{\text{o}}}$
Hence,
$\dfrac{\text{5 }\!\!\pi\!\!\text{ }}{\text{3}}$ radian$\text{=}\dfrac{\text{180}}{\text{ }\!\!\pi\!\!\text{ }}\text{ }\!\!\times\!\!\text{ }\dfrac{\text{5 }\!\!\pi\!\!\text{ }}{\text{3}}$ degree
$\text{=30}{{\text{0}}^{\text{o}}}$
(iv)$\dfrac{\text{7 }\!\!\pi\!\!\text{ }}{\text{6}}$
Ans: We know that,
$\pi $ radian$\text{=18}{{\text{0}}^{\text{o}}}$
Therefore $\text{1 radian =}{{\dfrac{\text{180}}{\text{ }\!\!\pi\!\!\text{ }}}^{\text{o}}}$
Hence,
$\dfrac{\text{7 }\!\!\pi\!\!\text{ }}{\text{6}}$ radian$\text{=}\dfrac{\text{180}}{\text{ }\!\!\pi\!\!\text{ }}\text{ }\!\!\times\!\!\text{ }\dfrac{\text{7 }\!\!\pi\!\!\text{ }}{\text{6}}$
$\text{=21}{{\text{0}}^{\text{o}}}$
3. A wheel makes $\text{360}$ revolutions in one minute. Through how many radians does it turn in one second?
Ans: Number of revolutions the wheel makes in $\text{1}$ minute$\text{=360}$
Number of revolutions the wheel make in $\text{1}$ second$\text{=}\dfrac{\text{360}}{\text{60}}$
$\text{=6}$
In one complete revolution, the wheel turns an angle of \[\text{2 }\!\!\pi\!\!\text{ }\] radian.
Hence, it will turn an angle of $\text{6 }\!\!\times\!\!\text{ 2 }\!\!\pi\!\!\text{ =12 }\!\!\pi\!\!\text{ }$ radian, in $\text{6}$ complete revolutions.
Therefore, the wheel turns an angle of $\text{12 }\!\!\pi\!\!\text{ }$ radian in one second.
4. Find the degree measure of the angle subtended at the centre of a circle of radius $\text{100}$cm by an arc of length $\text{22}$ cm.
(Use$\text{ }\!\!\pi\!\!\text{ =}\dfrac{\text{22}}{\text{7}}$ )
Ans: We know that,
in a circle of radius $\text{r}$ unit, if an angle $\text{ }\!\!\theta\!\!\text{ }$ radian at the centre is subtended by an arc of length $\text{l}$ unit then
$\text{ }\!\!\theta\!\!\text{ =}\dfrac{\text{l}}{\text{r}}$ ……(1)
Therefore,
Substituting $\text{r=100cm}$ ,\[\text{l=22cm}\] in the formula (1) , we have,
$\text{ }\!\!\theta\!\!\text{ =}\dfrac{\text{22}}{\text{100}}$ radian
Since $\text{1 radian=}\dfrac{\text{180}}{\text{ }\!\!\pi\!\!\text{ }}$
Therefore,
$\text{ }\!\!\theta\!\!\text{ =}\dfrac{\text{180}}{\text{ }\!\!\pi\!\!\text{ }}\text{ }\!\!\times\!\!\text{ }\dfrac{\text{22}}{\text{100}}$ degree
$\text{=}\dfrac{\text{180 }\!\!\times\!\!\text{ 7 }\!\!\times\!\!\text{ 22}}{\text{22 }\!\!\times\!\!\text{ 100}}$degree
$\text{=}\dfrac{\text{63}}{\text{5}}$ degree
$\text{=12}\dfrac{\text{3}}{\text{5}}$degree
Since ${{\text{1}}^{\text{o}}}\text{=60 }\!\!'\!\!\text{ }$ , we have,
$\text{ }\!\!\theta\!\!\text{ =1}{{\text{2}}^{\text{o}}}\text{36 }\!\!'\!\!\text{ }$
Hence , the required angle is $\text{1}{{\text{2}}^{\text{o}}}\text{36 }\!\!'\!\!\text{ }$.
5. In a circle of diameter $\text{40}$ cm, the length of a chord is $\text{20}$ cm. Find the length of minor arc of the chord.
Ans: Given that, diameter of the circle$=40$ cm
Hence Radius $\left( r \right)$ of the circle$=\dfrac{40}{2}cm$
$=20cm$
Let $\text{AB}$ be a chord of the circle whose length is $20$ cm.
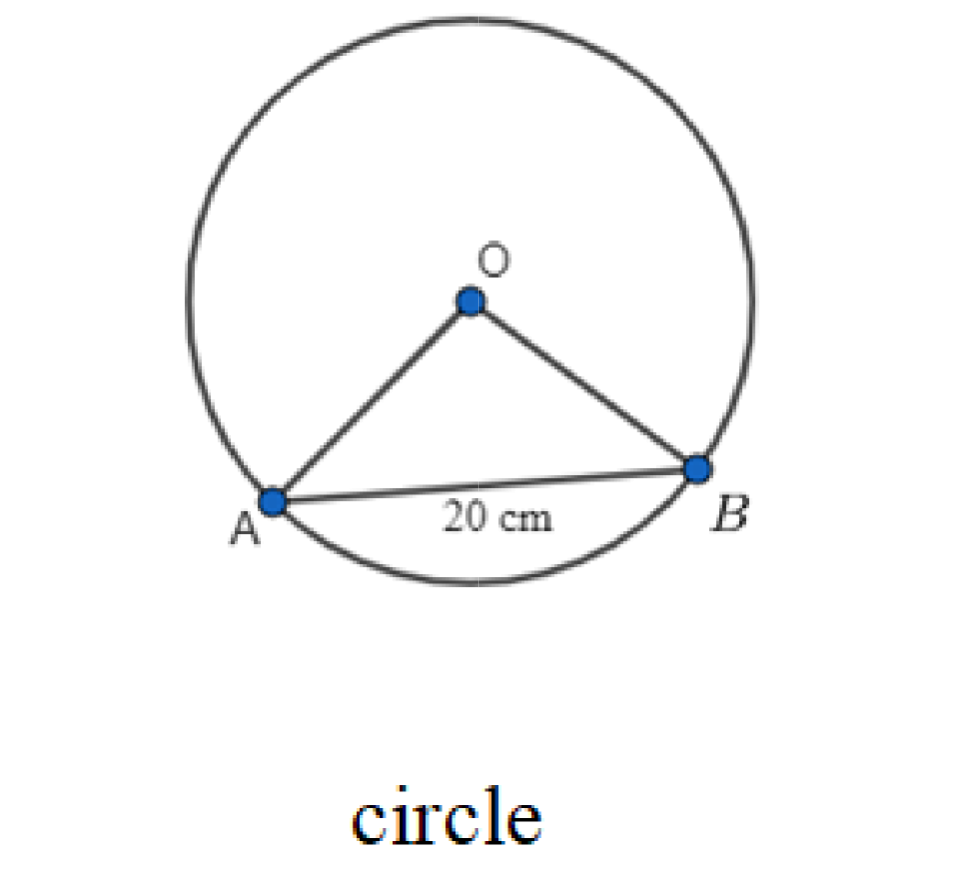
In $\Delta \text{OAB,}$
$\text{OA=OB}$
$=$ Radius of the circle
$\text{=20cm}$
Now also, $\text{AB=20cm}$
Therefore, $\Delta \text{OAB}$ is an equilateral triangle.
\[\therefore \text{ }\!\!\theta\!\!\text{ =6}{{\text{0}}^{\text{o}}}\]
$\text{=}\dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{3}}$ radian
We know that,
in a circle of radius $\text{r}$ unit, if an angle $\text{ }\!\!\theta\!\!\text{ }$ radian at the centre is subtended by an arc of length $\text{l}$ unit then
$\text{ }\!\!\theta\!\!\text{ =}\dfrac{\text{l}}{\text{r}}$ ……(1)
Substituting $\text{ }\!\!\theta\!\!\text{ =}\dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{3}}$ in the formula (1),
$\dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{3}}\text{=}\dfrac{\text{arc AB}}{\text{20}}$
$\text{arc AB=}\dfrac{\text{20 }\!\!\pi\!\!\text{ }}{\text{3}}\text{cm}$
Therefore, the length of the minor arc of the chord is $\dfrac{\text{20 }\!\!\pi\!\!\text{ }}{\text{3}}\text{cm}$ .
6. If in two circles, arcs of the same length subtend angles $\text{6}{{\text{0}}^{\text{o}}}$ and $\text{7}{{\text{5}}^{\text{o}}}$ at the centre, find the ratio of their radii.
Ans: Let the radii of the two circles be ${{\text{r}}_{\text{1}}}$ and ${{\text{r}}_{\text{2}}}$ . Let an arc of length ${{\text{l}}_{\text{1}}}$ subtends an angle of $\text{6}{{\text{0}}^{\text{o}}}$ at the centre of the circle of radius ${{\text{r}}_{\text{1}}}$ , whereas let an arc of length ${{\text{l}}_{\text{2}}}$ subtends an angle of $\text{7}{{\text{5}}^{\text{o}}}$ at the centre of the circle of radius ${{\text{r}}_{\text{2}}}$ .
Now, we have,
$\text{6}{{\text{0}}^{\text{o}}}\text{=}\dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{3}}$ radian and
${{75}^{\circ }}=\dfrac{5\pi }{12}$ radian
We know that,
in a circle of radius $\text{r}$ unit, if an angle $\text{ }\!\!\theta\!\!\text{ }$ radian at the centre is subtended by an arc of length $\text{l}$ unit then
\[\text{ }\!\!\theta\!\!\text{ =}\dfrac{\text{l}}{\text{r}}\]
$\text{l=r }\!\!\theta\!\!\text{ }$
Hence we obtain,
$\text{l=}\dfrac{{{\text{r}}_{\text{1}}}\text{ }\!\!\pi\!\!\text{ }}{\text{3}}$
and $\text{l=}\dfrac{{{\text{r}}_{\text{2}}}\text{5 }\!\!\pi\!\!\text{ }}{\text{12}}$
according to the ${{\text{l}}_{\text{1}}}\text{=}{{\text{l}}_{\text{2}}}$
thus we have,
$\dfrac{{{\text{r}}_{\text{1}}}\text{ }\!\!\pi\!\!\text{ }}{\text{3 }\!\!\pi\!\!\text{ }}\text{=}\dfrac{{{\text{r}}_{\text{2}}}\text{5 }\!\!\pi\!\!\text{ }}{\text{12}}$
${{\text{r}}_{\text{1}}}\text{=}\dfrac{{{\text{r}}_{\text{2}}}\text{5}}{\text{4}}$
$\dfrac{{{\text{r}}_{\text{1}}}}{{{\text{r}}_{\text{2}}}}\text{=}\dfrac{\text{5}}{\text{4}}$
Hence , the ratio of the radii is $\text{5:4}$ .
7. Find the angle in radian through which a pendulum swings if its length is $\text{75}$ cm and the tip describes an arc of length.
(i) $\text{10}$ cm
Ans: We know that,
in a circle of radius $\text{r}$ unit, if an angle $\text{ }\!\!\theta\!\!\text{ }$ radian at the centre is subtended by an arc of length $\text{l}$ unit then
$\text{ }\!\!\theta\!\!\text{ =}\dfrac{\text{l}}{\text{r}}$
Given that $\text{r=75cm}$
And here, $\text{l=10cm}$
Hence substituting the values in the formula,
$\text{ }\!\!\theta\!\!\text{ =}\dfrac{\text{10}}{\text{75}}$ radian
$\text{=}\dfrac{\text{2}}{\text{15}}$radian
(ii) $\text{15}$ cm
Ans: We know that,
in a circle of radius $\text{r}$ unit, if an angle $\text{ }\!\!\theta\!\!\text{ }$ radian at the centre is subtended by an arc of length $\text{l}$ unit then
$\text{ }\!\!\theta\!\!\text{ =}\dfrac{\text{l}}{\text{r}}$
Given that $\text{r=75cm}$
And here, $\text{l=15cm}$
Hence substituting the values in the formula,
$\text{ }\!\!\theta\!\!\text{ =}\dfrac{\text{15}}{\text{75}}$ radian
$\text{=}\dfrac{\text{1}}{\text{5}}$radian
(iii) $\text{21}$ cm
Ans: We know that,
in a circle of radius $\text{r}$ unit, if an angle $\text{ }\!\!\theta\!\!\text{ }$ radian at the centre is subtended by an arc of length $\text{l}$ unit then
$\text{ }\!\!\theta\!\!\text{ =}\dfrac{\text{l}}{\text{r}}$
And here, $\text{l=21cm}$
Hence substituting the values in the formula,
$\text{ }\!\!\theta\!\!\text{ =}\dfrac{\text{21}}{\text{75}}$ radian
$\text{=}\dfrac{\text{7}}{\text{25}}$radian
Exercise 3.2
1. Find the values of the other five trigonometric functions if $\text{cos x=-}\dfrac{\text{1}}{\text{2}}$ , $x$ lies in the third quadrant.
Ans: Here given that, $\text{cos x=-}\dfrac{\text{1}}{\text{2}}$
Therefore we have,
$\text{sec x=}\dfrac{\text{1}}{\text{cos x}}$
$\text{=}\dfrac{\text{1}}{\left( \text{-}\dfrac{\text{1}}{\text{2}} \right)}$
$\text{=-2}$
Now we know that,$\text{si}{{\text{n}}^{\text{2}}}\text{x+co}{{\text{s}}^{\text{2}}}\text{x=1}$
Therefore we have, $\text{si}{{\text{n}}^{\text{2}}}\text{x=1-co}{{\text{s}}^{\text{2}}}\text{x}$
Substituting $\text{cos x=-}\dfrac{\text{1}}{\text{2}}$ in the formula, we obtain,
$\text{si}{{\text{n}}^{\text{2}}}\text{x=1-}{{\left( \text{-}\dfrac{\text{1}}{\text{2}} \right)}^{\text{2}}}$
$\text{si}{{\text{n}}^{\text{2}}}\text{x=1-}\dfrac{\text{1}}{\text{4}}$
$\text{=}\dfrac{\text{3}}{\text{4}}$
$\text{sin x= }\!\!\pm\!\!\text{ }\dfrac{\sqrt{\text{3}}}{\text{2}}$
Since $\text{x}$ lies in the ${{\text{3}}^{\text{rd}}}$quadrant, the value of $\sin x$ will be negative.
$\text{sin x=-}\dfrac{\sqrt{\text{3}}}{\text{2}}$
Therefore, $\text{cosec x=}\dfrac{\text{1}}{\text{sin x}}$
$\text{=}\dfrac{\text{1}}{\left( \text{-}\dfrac{\sqrt{\text{3}}}{\text{2}} \right)}$
$\text{=-}\dfrac{\text{2}}{\sqrt{\text{3}}}$
Hence ,
$\text{tan x=}\dfrac{\text{sin x}}{\text{cos x}}$
$\text{=}\dfrac{\left( \text{-}\dfrac{\sqrt{\text{3}}}{\text{2}} \right)}{\left( \text{-}\dfrac{\text{1}}{\text{2}} \right)}$
$\text{=}\sqrt{\text{3}}$
And
$\text{cot x=}\dfrac{\text{1}}{\text{tan x}}$
$\text{=}\dfrac{\text{1}}{\sqrt{\text{3}}}$
2. Find the values of other five trigonometric functions if $\text{sin x=}\dfrac{\text{3}}{\text{5}}$ , $\text{x}$ lies in second quadrant.
Ans:
Here given that, $\text{sin x=}\dfrac{\text{3}}{\text{5}}$
Therefore we have,
$\text{cosec x=}\dfrac{\text{1}}{\text{sin x}}$
$=\dfrac{1}{\left( \dfrac{3}{5} \right)}$
$=\dfrac{5}{3}$
Now we know that , ${{\sin }^{2}}x+{{\cos }^{2}}x=1$
Therefore we have, $\text{co}{{\text{s}}^{\text{2}}}\text{x=1-si}{{\text{n}}^{\text{2}}}\text{x}$
Substituting $\sin x=\dfrac{3}{5}$ in the formula, we obtain,
$\text{co}{{\text{s}}^{\text{2}}}\text{x=1-}{{\left( \dfrac{\text{3}}{\text{5}} \right)}^{\text{2}}}$
$\text{co}{{\text{s}}^{\text{2}}}\text{x=1-}\dfrac{\text{9}}{\text{25}}$
$\text{=}\dfrac{\text{16}}{\text{25}}$
$\text{cos x= }\!\!\pm\!\!\text{ }\dfrac{\text{4}}{\text{5}}$
Since $x$ lies in the ${{2}^{nd}}$quadrant, the value of $\cos x$ will be negative.
$\text{cos x=-}\dfrac{\text{4}}{\text{5}}$
Therefore, $sec x=\dfrac{1}{\cos x}$
$\text{=}\dfrac{\text{1}}{\left( \text{-}\dfrac{\text{4}}{\text{5}} \right)}$
$\text{=-}\dfrac{\text{5}}{\text{4}}$
Hence ,
$\tan x=\dfrac{\sin x}{\cos x}$
$\text{=}\dfrac{\left( \dfrac{\text{3}}{\text{5}} \right)}{\left( \text{-}\dfrac{\text{4}}{\text{5}} \right)}$
$\text{=-}\dfrac{\text{3}}{\text{4}}$
And
$\cot x=\dfrac{1}{\tan x}$
$\text{=-}\dfrac{\text{4}}{\text{3}}$
3. Find the values of other five trigonometric functions if $\text{cot x=}\dfrac{\text{3}}{\text{4}}$ , $\text{x}$ lies in third quadrant.
Ans: Here given that, $\cot x=\dfrac{3}{4}$
Therefore we have,
$\tan x=\dfrac{1}{\cot x}$
$=\dfrac{1}{\left( \dfrac{3}{4} \right)}$
$=\dfrac{4}{3}$
Now we know that , \[\text{se}{{\text{c}}^{\text{2}}}\text{x-ta}{{\text{n}}^{\text{2}}}\text{x=1}\]
Therefore we have, $\text{se}{{\text{c}}^{\text{2}}}\text{x=1+ta}{{\text{n}}^{\text{2}}}\text{x}$
Substituting $\text{tan x=}\dfrac{\text{4}}{\text{3}}$ in the formula, we obtain,
${{\sec }^{2}}x=1+{{\left( \dfrac{4}{3} \right)}^{2}}$
$\text{se}{{\text{c}}^{\text{2}}}\text{x=1+}\dfrac{\text{16}}{\text{9}}$
$=\dfrac{25}{9}$
$\text{sec x= }\!\!\pm\!\!\text{ }\dfrac{\text{5}}{\text{3}}$
Since $x$ lies in the ${{3}^{rd}}$quadrant, the value of $\sec x$ will be negative.
$\text{sec x=-}\dfrac{\text{5}}{\text{3}}$
Therefore, $\cos x=\dfrac{1}{\sec x}$
$\text{=}\dfrac{\text{1}}{\left( \text{-}\dfrac{\text{5}}{\text{3}} \right)}$
$\text{=-}\dfrac{\text{3}}{\text{5}}$
Now , $\text{tan x=}\dfrac{\text{sin x}}{\text{cos x}}$
Therefore, $\text{sin x=tan xcos x}$
Hence we have, $\text{sin x=}\dfrac{\text{4}}{\text{3}}\text{ }\!\!\times\!\!\text{ }\left( \text{-}\dfrac{\text{3}}{\text{5}} \right)$
\[\text{=}\left( \text{-}\dfrac{\text{4}}{\text{5}} \right)\]
And
$\text{cosec x=}\dfrac{\text{1}}{\text{sin x}}$
$\text{=-}\dfrac{\text{5}}{\text{4}}$
4. Find the values of other five trigonometric functions if $\text{sec x=}\dfrac{\text{13}}{\text{5}}$ , $\text{x}$ lies in fourth quadrant.
Ans: Here given that, $\sec x=\dfrac{13}{5}$
Therefore we have,
$\cos x=\dfrac{1}{\sec x}$
$=\dfrac{1}{\left( \dfrac{13}{5} \right)}$
$=\dfrac{5}{13}$
Now we know that , $\text{se}{{\text{c}}^{\text{2}}}\text{x-ta}{{\text{n}}^{\text{2}}}\text{x=1}$
Therefore we have, $\text{ta}{{\text{n}}^{\text{2}}}\text{x=se}{{\text{c}}^{\text{2}}}\text{x-1}$
Substituting \[\text{sec x=}\dfrac{\text{13}}{\text{5}}\] in the formula, we obtain,
\[\text{ta}{{\text{n}}^{\text{2}}}\text{x=}{{\left( \dfrac{\text{13}}{\text{5}} \right)}^{\text{2}}}\text{-1}\]
$\text{ta}{{\text{n}}^{\text{2}}}\text{x=}\dfrac{\text{169}}{\text{25}}\text{-1}$
$\text{=}\dfrac{\text{144}}{\text{25}}$
\[\text{tanx= }\!\!\pm\!\!\text{ }\dfrac{\text{12}}{\text{5}}\]
Since $x$ lies in the ${{4}^{th}}$ quadrant, the value of $\tan x$ will be negative.
$\text{tan x=-}\dfrac{\text{12}}{\text{5}}$
Therefore, \[\text{cot x=}\dfrac{\text{1}}{\text{tan x}}\]
$\text{=-}\dfrac{\text{5}}{\text{12}}$
Now , $\text{tan x=}\dfrac{\text{sin x}}{\text{cos x}}$
Therefore, $\text{sin x=tan xcos x}$
Hence we have, $\text{sin x=}\dfrac{\text{5}}{\text{13}}\text{ }\!\!\times\!\!\text{ }\left( \text{-}\dfrac{\text{12}}{\text{5}} \right)$
$\text{=}\left( \text{-}\dfrac{\text{12}}{\text{13}} \right)$
And
$\text{cosec x=}\dfrac{\text{1}}{\text{sin x}}$
$\text{=-}\dfrac{\text{13}}{\text{12}}$
5. Find the values of other five trigonometric functions if $\text{tan x=-}\dfrac{\text{5}}{\text{12}}$ , $\text{x}$ lies in second quadrant.
Ans: Here given that, $\text{tan x=-}\dfrac{\text{5}}{\text{12}}$
Therefore we have,
$\text{cot x=}\dfrac{\text{1}}{\text{tan x}}$
$\text{=}\dfrac{\text{1}}{\left( \text{-}\dfrac{\text{5}}{\text{12}} \right)}$
$\text{=-}\dfrac{\text{12}}{\text{5}}$
Now we know that , $\text{se}{{\text{c}}^{\text{2}}}\text{x-ta}{{\text{n}}^{\text{2}}}\text{x=1}$
Therefore we have, $\text{se}{{\text{c}}^{\text{2}}}\text{x=1+ta}{{\text{n}}^{\text{2}}}\text{x}$
Substituting $\text{tan x=-}\dfrac{\text{5}}{\text{12}}$ in the formula, we obtain,
$\text{se}{{\text{c}}^{\text{2}}}\text{x=1+}{{\left( \text{-}\dfrac{\text{5}}{\text{12}} \right)}^{\text{2}}}$
$\text{se}{{\text{c}}^{\text{2}}}\text{x=1+}\dfrac{\text{25}}{\text{144}}$
$=\dfrac{169}{144}$
$\text{sec x= }\!\!\pm\!\!\text{ }\dfrac{\text{13}}{\text{12}}$
Since $x$ lies in the ${{2}^{nd}}$ quadrant, the value of $\sec x$ will be negative.
$\text{sec x=-}\dfrac{\text{13}}{\text{12}}$
Therefore, $\text{cos x=}\dfrac{\text{1}}{\text{sec x}}$
$\text{=-}\dfrac{\text{12}}{\text{13}}$
Now , $\text{tan x=}\dfrac{\text{sin x}}{\text{cos x}}$
Therefore, $\text{sin x=tan xcos x}$
Hence we have, $\text{sin x=}\left( \text{-}\dfrac{\text{5}}{\text{12}} \right)\text{ }\!\!\times\!\!\text{ }\left( \text{-}\dfrac{\text{12}}{\text{13}} \right)$
$=\left( \dfrac{5}{13} \right)$
And
$\text{cosec x=}\dfrac{\text{1}}{\text{sin x}}$
$\text{=}\dfrac{\text{13}}{\text{5}}$
6. Find the value of the trigonometric function $\text{sin76}{{\text{5}}^{\text{o}}}$ .
Ans: We know that the values of $\sin x$ repeat after an interval of $2\pi $ or ${{360}^{\circ }}$ .
Therefore we can write,
$\text{sin76}{{\text{5}}^{\text{o}}}\text{=sin}\left( \text{2 }\!\!\times\!\!\text{ 36}{{\text{0}}^{\text{o}}}\text{+4}{{\text{5}}^{\text{o}}} \right)$
$\text{=sin4}{{\text{5}}^{\text{o}}}$
$\text{=}\dfrac{\text{1}}{\sqrt{\text{2}}}\text{.}$
7. Find the value of the trigonometric function $\text{cosec}\left( \text{-141}{{\text{0}}^{\text{o}}} \right)$
Ans: We know that the values of $\text{cosec x}$ repeat after an interval of $\text{2 }\!\!\pi\!\!\text{ }$ or ${{360}^{\circ }}$ .
Therefore we can write,
$\text{cosec}\left( \text{-141}{{\text{0}}^{\text{o}}} \right)\text{=cosec}\left( \text{-141}{{\text{0}}^{\text{o}}}\text{+4 }\!\!\times\!\!\text{ 36}{{\text{0}}^{\text{o}}} \right)$
$\text{=cosec}\left( \text{-141}{{\text{0}}^{\text{o}}}\text{+144}{{\text{0}}^{\text{o}}} \right)$
$\text{=cosec3}{{\text{0}}^{\text{o}}}$
$=2$
8. Find the value of the trigonometric function $\text{tan}\dfrac{\text{19 }\!\!\pi\!\!\text{ }}{\text{3}}$ .
Ans: We know that the values of $\text{tan x}$ repeat after an interval of $\text{ }\!\!\pi\!\!\text{ }$ or \[{{180}^{\circ }}\].
Therefore we can write,
$\text{tan}\dfrac{\text{19 }\!\!\pi\!\!\text{ }}{\text{3}}\text{=tan6}\dfrac{\text{1}}{\text{3}}\text{ }\!\!\pi\!\!\text{ }$
$\text{=tan}\left( \text{6 }\!\!\pi\!\!\text{ +}\dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{3}} \right)$
\[\text{=tan}\dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{3}}\]
$\text{=}\sqrt{\text{3}}$
9. Find the value of the trigonometric function $\text{sin}\left( \text{-}\dfrac{\text{11 }\!\!\pi\!\!\text{ }}{\text{3}} \right)$
Ans: We know that the values of $\text{sin x}$ repeat after an interval of $\text{2 }\!\!\pi\!\!\text{ }$ or ${{360}^{\circ }}$ .
Therefore we can write,
$\text{sin}\left( \text{-}\dfrac{\text{11 }\!\!\pi\!\!\text{ }}{\text{3}} \right)\text{=sin}\left( \text{-}\dfrac{\text{11 }\!\!\pi\!\!\text{ }}{\text{3}}\text{+2 }\!\!\times\!\!\text{ 2 }\!\!\pi\!\!\text{ } \right)$
$\text{=sin}\left( \dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{3}} \right)$
$=\dfrac{\sqrt{3}}{2}$
10. Find the value of the trigonometric function $\text{cot}\left( \text{-}\dfrac{\text{15 }\!\!\pi\!\!\text{ }}{\text{4}} \right)$
Ans: We know that the values of $\text{cot x}$ repeat after an interval of $\text{ }\!\!\pi\!\!\text{ }$ or \[{{180}^{\circ }}\].
Therefore we can write,
$\text{cot}\left( \text{-}\dfrac{\text{15 }\!\!\pi\!\!\text{ }}{\text{4}} \right)\text{=cot}\left( \text{-}\dfrac{\text{15 }\!\!\pi\!\!\text{ }}{\text{4}}\text{+4 }\!\!\pi\!\!\text{ } \right)$
$\text{=cot}\dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{4}}$
$=1$
Exercise 3.3
1. Prove that $\text{si}{{\text{n}}^{\text{2}}}\dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{6}}\text{+co}{{\text{s}}^{\text{2}}}\dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{3}}\text{-ta}{{\text{n}}^{\text{2}}}\dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{4}}\text{=-}\dfrac{\text{1}}{\text{2}}$
Ans: Substituting the values of \[\text{sin}\dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{6}}\text{,cos}\dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{6}}\text{,tan}\dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{4}}\] on left hand side,
$\text{si}{{\text{n}}^{\text{2}}}\dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{6}}\text{+co}{{\text{s}}^{\text{2}}}\dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{3}}\text{-ta}{{\text{n}}^{\text{2}}}\dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{4}}\text{=}{{\left( \dfrac{\text{1}}{\text{2}} \right)}^{\text{2}}}\text{+}{{\left( \dfrac{\text{1}}{\text{2}} \right)}^{\text{2}}}\text{-}{{\left( \text{1} \right)}^{\text{2}}}$
\[\text{=}\dfrac{\text{1}}{\text{4}}\text{+}\dfrac{\text{1}}{\text{4}}\text{-1}\]
$=-\dfrac{1}{2}$
$=$ R.H.S.
Hence proved.
2. Prove that $\text{2si}{{\text{n}}^{\text{2}}}\dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{6}}\text{+cose}{{\text{c}}^{\text{2}}}\dfrac{\text{7 }\!\!\pi\!\!\text{ }}{\text{6}}\text{co}{{\text{s}}^{\text{2}}}\dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{3}}\text{=}\dfrac{\text{3}}{\text{2}}$
Ans: Substituting the values of $\text{sin}\dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{6}}\text{,cosec}\dfrac{\text{7 }\!\!\pi\!\!\text{ }}{\text{6}}\text{,cos}\dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{3}}$ on left hand side,
L.H.S.$\text{=2si}{{\text{n}}^{\text{2}}}\dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{6}}\text{+cose}{{\text{c}}^{\text{2}}}\dfrac{\text{7 }\!\!\pi\!\!\text{ }}{\text{6}}\text{co}{{\text{s}}^{\text{2}}}\dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{3}}$
$\text{=2}{{\left( \dfrac{\text{1}}{\text{2}} \right)}^{\text{2}}}\text{+cose}{{\text{c}}^{\text{2}}}\left( \text{ }\!\!\pi\!\!\text{ +}\dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{6}} \right){{\left( \dfrac{\text{1}}{\text{2}} \right)}^{\text{2}}}$
$\text{=2 }\!\!\times\!\!\text{ }\dfrac{\text{1}}{\text{4}}\text{+}{{\left( \text{-cosec}\dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{6}} \right)}^{\text{2}}}\left( \dfrac{\text{1}}{\text{4}} \right)$
$\text{=}\dfrac{\text{1}}{\text{2}}\text{+}{{\left( \text{-2} \right)}^{\text{2}}}\left( \dfrac{\text{1}}{\text{4}} \right)$
Since $\text{cosec x}$ repeat its value after an interval of $\text{2 }\!\!\pi\!\!\text{ }$ ,
we have, $\text{cosec}\dfrac{\text{7 }\!\!\pi\!\!\text{ }}{\text{6}}\text{=-cosec}\dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{6}}$
L.H.S $=\dfrac{1}{2}+\dfrac{4}{4}$
$=\dfrac{3}{2}$
$=$ R.H.S.
Hence proved.
3. Prove that $\text{co}{{\text{t}}^{\text{2}}}\dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{6}}\text{+cosec}\dfrac{\text{5 }\!\!\pi\!\!\text{ }}{\text{6}}\text{+3ta}{{\text{n}}^{\text{2}}}\dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{6}}\text{=6}$
Ans: Substituting the values of $\text{cot}\dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{6}}\text{,cosec}\dfrac{\text{5 }\!\!\pi\!\!\text{ }}{\text{6}}\text{,tan}\dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{6}}$ on left hand side,
L.H.S.$\text{=co}{{\text{t}}^{\text{2}}}\dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{6}}\text{+cosec}\dfrac{\text{5 }\!\!\pi\!\!\text{ }}{\text{6}}\text{+3ta}{{\text{n}}^{\text{2}}}\dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{6}}$
$\text{=}{{\left( \sqrt{\text{3}} \right)}^{\text{2}}}\text{+cosec}\left( \text{ }\!\!\pi\!\!\text{ -}\dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{6}} \right)\text{+3}{{\left( \dfrac{\text{1}}{\sqrt{\text{3}}} \right)}^{\text{2}}}$
$\text{=3+cosec}\dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{6}}\text{+3 }\!\!\times\!\!\text{ }\dfrac{\text{1}}{\text{3}}$
Since $\text{cosec x}$ repeat its value after an interval of $\text{2 }\!\!\pi\!\!\text{ }$ ,
we have, $\text{cosec}\dfrac{\text{5 }\!\!\pi\!\!\text{ }}{\text{6}}\text{=cosec}\dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{6}}$
L.H.S $=3+2+1$
$=1$
$=$ R.H.S.
Hence proved.
4. Prove that $\text{2si}{{\text{n}}^{\text{2}}}\dfrac{\text{3 }\!\!\pi\!\!\text{ }}{\text{4}}\text{+2co}{{\text{s}}^{\text{2}}}\dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{4}}\text{+2se}{{\text{c}}^{\text{2}}}\dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{3}}\text{=10}$
Ans:
Substituting the values of $\text{sin}\dfrac{\text{3 }\!\!\pi\!\!\text{ }}{\text{4}}\text{,cos}\dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{4}}\text{,sec}\dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{3}}$ on left hand side,
L.H.S.$\text{=2si}{{\text{n}}^{\text{2}}}\dfrac{\text{3 }\!\!\pi\!\!\text{ }}{\text{4}}\text{+2co}{{\text{s}}^{\text{2}}}\dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{4}}\text{+2se}{{\text{c}}^{\text{2}}}\dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{3}}$
$\text{=2}{{\left\{ \text{sin}\left( \text{ }\!\!\pi\!\!\text{ -}\dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{4}} \right) \right\}}^{\text{2}}}\text{+2}{{\left( \dfrac{\text{1}}{\sqrt{\text{2}}} \right)}^{\text{2}}}\text{+2}{{\left( \text{2} \right)}^{\text{2}}}$
$\text{=2}{{\left\{ \text{sin}\dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{4}} \right\}}^{\text{2}}}\text{+2 }\!\!\times\!\!\text{ }\dfrac{\text{1}}{\text{2}}\text{+8}$
Since $\text{sin x}$ repeat its value after an interval of \[\text{2 }\!\!\pi\!\!\text{ }\] ,
we have, \[\text{sin}\dfrac{\text{3 }\!\!\pi\!\!\text{ }}{\text{4}}\text{=sin}\dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{4}}\]
L.H.S $=1+1+8$
$=10$
$=$ R.H.S.
Hence proved.
5. Find the value of :
(i) $\text{sin7}{{\text{5}}^{\text{o}}}$
Ans: We have,
$\text{sin7}{{\text{5}}^{\text{o}}}\text{=sin(4}{{\text{5}}^{\text{o}}}\text{+3}{{\text{0}}^{\text{o}}}\text{)}$
$\text{=sin4}{{\text{5}}^{\text{o}}}\text{cos3}{{\text{0}}^{\text{o}}}\text{+cos4}{{\text{5}}^{\text{o}}}\text{sin3}{{\text{0}}^{\text{o}}}$
Since we know that, $\text{sin}\left( \text{x+y} \right)\text{=sin x cos y+cos x sin y}$
Therefore we have,
$Sin 75^o = \dfrac{1}{\sqrt 2}\times \dfrac{\sqrt 3}{2} + \dfrac{1}{\sqrt 2}\times\dfrac{1}{2}$
$Sin 75^o = \dfrac{{\sqrt 3}+1}{2\sqrt 2}$
(ii) $\text{tan1}{{\text{5}}^{\text{o}}}$
Ans: We have,
\[\text{tan1}{{\text{5}}^{\text{o}}}\text{=tan}\left( \text{4}{{\text{5}}^{\text{o}}}\text{-3}{{\text{0}}^{\text{o}}} \right)\]
$\text{=}\dfrac{\text{tan4}{{\text{5}}^{\text{o}}}\text{-tan3}{{\text{0}}^{\text{o}}}}{\text{1+tan4}{{\text{5}}^{\text{o}}}\text{tan3}{{\text{0}}^{\text{o}}}}$
Since we know, $\text{tan}\left( \text{x-y} \right)\text{=}\dfrac{\text{tan x-tan y}}{\text{1+tan x tan y}}$
Therefore we have,
$\text{tan1}{{\text{5}}^{\text{o}}}\text{=}\dfrac{\text{1-}\dfrac{\text{1}}{\sqrt{\text{3}}}}{\text{1+1}\left( \dfrac{\text{1}}{\sqrt{\text{3}}} \right)}$
$\text{=}\dfrac{\dfrac{\sqrt{\text{3}}\text{-1}}{\sqrt{\text{3}}}}{\dfrac{\sqrt{\text{3}}\text{+1}}{\sqrt{\text{3}}}}$
$\text{=}\dfrac{\sqrt{\text{3}}\text{-1}}{\sqrt{\text{3}}\text{+1}}$
$\text{=}\dfrac{{{\left( \sqrt{\text{3}}\text{-1} \right)}^{\text{2}}}}{\left( \sqrt{\text{3}}\text{+1} \right)\left( \sqrt{\text{3}}\text{-1} \right)}$
Further computing we have,
$\text{tan1}{{\text{5}}^{\text{o}}}\text{=}\dfrac{\text{3+1-2}\sqrt{\text{3}}}{{{\left( \sqrt{\text{3}} \right)}^{\text{2}}}\text{-}{{\left( \text{1} \right)}^{\text{2}}}}$
\[\text{=}\dfrac{\text{4-2}\sqrt{\text{3}}}{\text{3-1}}\]
\[\text{=2-}\sqrt{\text{3}}\]
6. Prove that $\text{cos}\left( \dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{4}}\text{-x} \right)\text{cos}\left( \dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{4}}\text{-y} \right)\text{-sin}\left( \dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{4}}\text{-x} \right)\text{sin}\left( \dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{4}}\text{-y} \right)\text{=sin}\left( \text{x+y} \right)$
Ans: We know that, $\text{cos}\left( \text{x+y} \right)\text{=cos xcos y-sin xsin y}$
$\text{cos}\left( \dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{4}}\text{-x} \right)\text{cos}\left( \dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{4}}\text{-y} \right)\text{-sin}\left( \dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{4}}\text{-x} \right)\text{sin}\left( \dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{4}}\text{-y} \right)\text{=cos}\left[ \dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{4}}\text{-x+}\dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{4}}\text{-y} \right]$
$\text{=cos}\left[ \dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{2}}\text{-}\left( \text{x+y} \right) \right]$
$\text{=sin}\left( \text{x+y} \right)$
L.H.S $=$ R.H.S.
Hence proved.
7. Prove that $\dfrac{\text{tan}\left( \dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{4}}\text{+x} \right)}{\text{tan}\left( \dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{4}}\text{-x} \right)}\text{=}{{\left( \dfrac{\text{1+tanx}}{\text{1-tanx}} \right)}^{\text{2}}}$
Ans: We know that ,$\text{tan}\left( \text{A+B} \right)\text{=}\dfrac{\text{tan A+tan B}}{\text{1-tan Atan B}}$
and $\text{tan}\left( \text{A-B} \right)\text{=}\dfrac{\text{tan A-tan B}}{\text{1+tan Atan B}}$
L.H.S.$\text{=}\dfrac{\text{tan}\left( \dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{4}}\text{+x} \right)}{\text{tan}\left( \dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{4}}\text{-x} \right)}$
Using the above formula,
$\text{L}\text{.H}\text{.S=}\dfrac{\left( \dfrac{\text{tan}\dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{4}}\text{+tanx}}{\text{1-tan}\dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{4}}\text{tanx}} \right)}{\dfrac{\text{tan}\dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{4}}\text{-tanx}}{\text{1+tan}\dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{4}}\text{tanx}}}$
$\text{=}\dfrac{\left( \dfrac{\text{1+tan x}}{\text{1-tan x}} \right)}{\left( \dfrac{\text{1-tan x}}{\text{1+tan x}} \right)}$ [ substituting $\text{tan}\dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{4}}\text{=1}$ ]
$\text{=}{{\left( \dfrac{\text{1+tan x}}{\text{1-tan x}} \right)}^{\text{2}}}$
$=$ R.H.S.
Hence proved.
8. Prove that $\dfrac{\text{cos}\left( \text{ }\!\!\pi\!\!\text{ +x} \right)\text{cos}\left( \text{-x} \right)}{\text{sin}\left( \text{ }\!\!\pi\!\!\text{ -x} \right)\text{cos}\left( \dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{2}}\text{+x} \right)}\text{=co}{{\text{t}}^{\text{2}}}\text{x}$
Ans: Observe that $\text{cos x}$ repeats same value after an interval $\text{2 }\!\!\pi\!\!\text{ }$
and $\text{sin x}$ repeats same value after an interval $\text{2 }\!\!\pi\!\!\text{ }$.
L.H.S.$\text{=}\dfrac{\text{cos}\left( \text{ }\!\!\pi\!\!\text{ +x} \right)\text{cos}\left( \text{-x} \right)}{\text{sin}\left( \text{ }\!\!\pi\!\!\text{ -x} \right)\text{cos}\left( \dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{2}}\text{+x} \right)}$
$\text{=}\dfrac{\left[ \text{-cos x} \right]\left[ \text{cos x} \right]}{\left( \text{sin x} \right)\left( \text{-sin x} \right)}$
$\text{=}\dfrac{\text{-co}{{\text{s}}^{\text{2}}}\text{x}}{\text{-si}{{\text{n}}^{\text{2}}}\text{x}}$
$\text{=co}{{\text{t}}^{\text{2}}}\text{x}$
Hence proved.
9. Prove that,
$\text{Cos}\left( \dfrac{\text{3 }\!\!\pi\!\!\text{ }}{\text{2}}\text{+x} \right)\text{Cos}\left( \text{2 }\!\!\pi\!\!\text{ +x} \right)\left[ \text{cot}\left( \dfrac{\text{3 }\!\!\pi\!\!\text{ }}{\text{2}}\text{-x} \right)\text{+cot}\left( \text{2 }\!\!\pi\!\!\text{ +x} \right) \right]\text{=1}$
Ans: We know that $\text{cot x}$ repeats same value after an interval $2\pi $ .
L.H.S.$=Cos\left( \dfrac{3\pi }{2}+x \right)Cos\left( 2\pi +x \right)\left[ cot\left( \dfrac{3\pi }{2}-x \right)+cot\left( 2\pi +x \right) \right]$
$\text{=sin x cos x}\left[ \text{tan x+cot x} \right]$
Substituting $\text{tan x=}\dfrac{\text{sin x}}{\text{cos x}}$ and
$\text{cot x=}\dfrac{\text{cos x}}{\text{sin x}}$ ,
$\text{L}\text{.H}\text{.S=sin xcos x}\left( \dfrac{\text{sin x}}{\text{cos x}}\text{+}\dfrac{\text{cos x}}{\text{sin x}} \right)$
$\text{=}\left( \text{sin x cos x} \right)\left[ \dfrac{\text{si}{{\text{n}}^{\text{2}}}\text{x+co}{{\text{s}}^{\text{2}}}\text{x}}{\text{sin x cos x}} \right]$
$\text{=1}$
$\text{=}$ R.H.S.
Hence proved.
10. Prove that $\text{sin}\left( \text{n+1} \right)\text{xsin}\left( \text{n+2} \right)\text{x+cos (n+1)x cos (n+2)x=cos x}$
Ans: We know that , $\text{cos}\left( \text{x-y} \right)\text{=cosxcosy+sinxsiny}$
L.H.S.$\text{=sin}\left( \text{n+1} \right)\text{xsin}\left( \text{n+2} \right)\text{x+cos (n+1)x cos (n+2)x}$
$\text{=cos}\left[ \left( \text{n+1} \right)\text{x-}\left( \text{n+2} \right)\text{x} \right]$
$\text{=cos}\left( \text{-x} \right)$
$\text{=cosx}$
$=$ R.H.S.
11. Prove that $\text{cos}\left( \dfrac{\text{3 }\!\!\pi\!\!\text{ }}{\text{4}}\text{+x} \right)\text{-cos}\left( \dfrac{\text{3 }\!\!\pi\!\!\text{ }}{\text{4}}\text{-x} \right)\text{=-}\sqrt{\text{2}}\text{sinx}$
Ans: We know that , $\text{cos A-cos B=-2sin}\left( \dfrac{\text{A+B}}{\text{2}} \right)\text{.sin}\left( \dfrac{\text{A-B}}{\text{2}} \right)$
$\therefore $ L.H.S.$\text{=cos}\left( \dfrac{\text{3 }\!\!\pi\!\!\text{ }}{\text{4}}\text{+x} \right)\text{-cos}\left( \dfrac{\text{3 }\!\!\pi\!\!\text{ }}{\text{4}}\text{-x} \right)$
$\text{=-2sin}\left\{ \dfrac{\left( \dfrac{\text{3 }\!\!\pi\!\!\text{ }}{\text{4}}\text{+x} \right)\text{+}\left( \dfrac{\text{3 }\!\!\pi\!\!\text{ }}{\text{4}}\text{-x} \right)}{\text{2}} \right\}\text{.sin}\left\{ \dfrac{\left( \dfrac{\text{3 }\!\!\pi\!\!\text{ }}{\text{4}}\text{+x} \right)\text{-}\left( \dfrac{\text{3 }\!\!\pi\!\!\text{ }}{\text{4}}\text{-x} \right)}{\text{2}} \right\}$
$\text{=-2sin}\left( \dfrac{\text{3 }\!\!\pi\!\!\text{ }}{\text{4}} \right)\text{sin x}$
Since $\text{sin x}$ repeats the same value after an interval $\text{2 }\!\!\pi\!\!\text{ }$ ,
we have, $\text{sin}\left( \dfrac{\text{3 }\!\!\pi\!\!\text{ }}{\text{4}} \right)\text{=sin}\left( \text{ }\!\!\pi\!\!\text{ -}\dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{4}} \right)$
therefore,
$\text{L}\text{.H}\text{.S=-2sin}\dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{4}}\text{sin x}$
$\text{=-2 }\!\!\times\!\!\text{ }\dfrac{\text{1}}{\sqrt{\text{2}}}\text{ }\!\!\times\!\!\text{ sinx}$
$\text{=-}\sqrt{\text{2}}\text{sin x}$
$\text{=}$ R.H.S.
Hence proved.
12. Prove that $\text{si}{{\text{n}}^{\text{2}}}\text{6x-si}{{\text{n}}^{\text{2}}}\text{4x=sin 2x sin 10x}$
Ans: We know that,$\text{sinA+sinB=2sin}\left( \dfrac{\text{A+B}}{\text{2}} \right)\text{cos}\left( \dfrac{\text{A-B}}{\text{2}} \right)$
And $\text{sin A-sin B=2cos}\left( \dfrac{\text{A+B}}{\text{2}} \right)\text{sin}\left( \dfrac{\text{A-B}}{\text{2}} \right)$
$\therefore $ L.H.S.$\text{=si}{{\text{n}}^{\text{2}}}\text{6x-si}{{\text{n}}^{\text{2}}}\text{4xa}$
$\text{=}\left( \text{sin 6x+sin 4x} \right)\left( \text{sin 6x-sin 4x} \right)$
$\text{=}\left[ \text{2sin}\left( \dfrac{\text{6x+4x}}{\text{2}} \right)\text{cos}\left( \dfrac{\text{6x-4x}}{\text{2}} \right) \right]\left[ \text{2cos}\left( \dfrac{\text{6x+4x}}{\text{2}} \right)\text{.sin}\left( \dfrac{\text{6x-4x}}{\text{2}} \right) \right]$
$\text{=}\left( \text{2sin 5x cos x} \right)\left( \text{2cos 5x sin x} \right)$
Now we know that, $\text{sin 2x=2sin x cos x}$ ,
Therefore we have,
$\text{L}\text{.H}\text{.S=}\left( \text{2sin 5x cos 5x} \right)\left( \text{2sin x cos x} \right)$
$\text{=sin 10x sin 2x}$
$\text{=}$ R.H.S.
13. Prove that $\text{co}{{\text{s}}^{\text{2}}}\text{2x-co}{{\text{s}}^{\text{2}}}\text{6x=sin 4x sin 8x}$
Ans: We know that,
$\text{cos A+cos B=2cos}\left( \dfrac{\text{A+B}}{\text{2}} \right)\text{cos}\left( \dfrac{\text{A-B}}{\text{2}} \right)$
And $\text{cos A-cos B=-2sin}\left( \dfrac{\text{A+B}}{\text{2}} \right)\text{sin}\left( \dfrac{\text{A-B}}{\text{2}} \right)$
L.H.S.$\text{=co}{{\text{s}}^{\text{2}}}\text{2x-co}{{\text{s}}^{\text{2}}}\text{6x}$
$\text{=}\left( \text{cos 2x+cos 6x} \right)\left( \text{cos 2x-6x} \right)$
$\text{=}\left[ \text{2cos}\left( \dfrac{\text{2x+6x}}{\text{2}} \right)\text{cos}\left( \dfrac{\text{2x-6x}}{\text{2}} \right) \right]\left[ \text{-2sin}\left( \dfrac{\text{2x+6x}}{\text{2}} \right)\text{sin}\left( \dfrac{\text{2x-6x}}{\text{2}} \right) \right]$
Further computing, we have,
$\text{L}\text{.H}\text{.S=}\left[ \text{2cos 4x cos}\left( \text{-2x} \right) \right]\left[ \text{-2sin 4xsin}\left( \text{-2x} \right) \right]$
$\text{=}\left[ \text{2cos 4x cos 2x} \right]\left[ \text{-2sin 4x}\left( \text{-sin 2x} \right) \right]$
$\text{=}\left( \text{2sin 4x cos 4x} \right)\left( \text{2sin 2xcos 2x} \right)$
Now we know that, $\text{sin 2x=2sin x cos x}$
Therefore we have,
$\text{L}\text{.H}\text{.S=sin 8x sin 4x}$
$\text{=}$ R.H.S.
.Hence proved.
14. Prove that $\text{sin 2x+2sin 4x+sin6=4co}{{\text{s}}^{\text{2}}}\text{xsin 4x}$
Ans: We know that, \[\text{sin A+sin B=2sin}\left( \dfrac{\text{A+B}}{\text{2}} \right)\text{cos}\left( \dfrac{\text{A-B}}{\text{2}} \right)\]
L.H.S.$\text{=sin 2x+2sin 4x+sin 6x}$
. $\text{=}\left[ \text{sin 2x+sin 6x} \right]\text{+2sin 4x}$
$\text{=}\left[ \text{2sin}\left( \dfrac{\text{2x+6x}}{\text{2}} \right)\text{cos}\left( \dfrac{\text{2x-6x}}{\text{2}} \right) \right]\text{+2sin4x}$
$\text{=2sin 4xcos}\left( \text{-2x} \right)\text{+2sin 4x}$
Further computing,
We have, $\text{L}\text{.H}\text{.S=2sin 4x cos 2x+2sin 4x}$
$\text{=2sin 4x}\left( \text{cos 2x+1} \right)$
Now we know that, $\text{cos 2x+1=2co}{{\text{s}}^{\text{2}}}\text{x}$
Therefore we have,
$\text{L}\text{.H}\text{.S=2sin 4x}\left( \text{2co}{{\text{s}}^{\text{2}}}\text{x} \right)$
$\text{=4co}{{\text{s}}^{\text{2}}}\text{xsin 4x}$
= R.H.S.
Hence proved.
15. Prove that $\text{cot 4x}\left( \text{sin 5x+sin 3x} \right)\text{=cot x}\left( \text{sin 5x-sin 3x} \right)$
Ans: We know that, $\text{sin A+sin B=2sin}\left( \dfrac{\text{A+B}}{\text{2}} \right)\text{cos}\left( \dfrac{\text{A-B}}{\text{2}} \right)$
L.H.S.$\text{=cot 4x}\left( \text{sin 5x+sin 3x} \right)$
$\text{=}\dfrac{\text{cot 4x}}{\text{sin 4x}}\left[ \text{2sin}\left( \dfrac{\text{5x+3x}}{\text{2}} \right)\text{cos}\left( \dfrac{\text{5x+3x}}{\text{2}} \right) \right]$
$\text{=}\left( \dfrac{\text{cos 4x}}{\text{sin 4x}} \right)\left[ \text{2sin 4x cos x} \right]$
$\text{=2cos 4x cos x}$
Now also ,we know that, $\text{sin A-sin B=2cos}\left( \dfrac{\text{A+B}}{\text{2}} \right)\text{sin}\left( \dfrac{\text{A-B}}{\text{2}} \right)$
R.H.S.$\text{=cot x}\left( \text{sin 5x-sin 3x} \right)$
$\text{=}\dfrac{\text{cos x}}{\text{sin x}}\left[ \text{2cos}\left( \dfrac{\text{5x+3x}}{\text{2}} \right)\text{sin}\left( \dfrac{\text{5x-3x}}{\text{2}} \right) \right]$
$\text{=}\dfrac{\text{cos x}}{\text{sin x}}\left[ \text{2cos 4x sin x} \right]$
$\text{=2cos 4x cos x}$
Therefore , we can conclude that,
L.H.S.=R.H.S.
Hence proved.
16. Prove that $\dfrac{\text{cos 9x-cos 5x}}{\text{sin 17x-sin 3x}}\text{=-}\dfrac{\text{sin 2x}}{\text{cos 10x}}$
Ans: We know that,
$\text{cos A-cos B=-2sin}\left( \dfrac{\text{A+B}}{\text{2}} \right)\text{sin}\left( \dfrac{\text{A-B}}{\text{2}} \right)$
And $\text{sin A-sin B=2cos}\left( \dfrac{\text{A+B}}{\text{2}} \right)\text{sin}\left( \dfrac{\text{A-B}}{\text{2}} \right)$
L.H.S.$\text{=}\dfrac{\text{cos 9x-cos 5x}}{\text{sin 17x-sin 3x}}$
\[\text{=}\dfrac{\text{-2sin}\left( \dfrac{\text{9x+5x}}{\text{2}} \right)\text{.sin}\left( \dfrac{\text{9x-5x}}{\text{2}} \right)}{\text{2cos}\left( \dfrac{\text{17x+3x}}{\text{2}} \right)\text{.sin}\left( \dfrac{\text{17x-3x}}{\text{2}} \right)}\] (following the formula)
$\text{=}\dfrac{\text{-2sin 7x}\text{.sin 2x}}{\text{2cos 10x}\text{.sin 7x}}$
$\text{=-}\dfrac{\text{sin 2x}}{\text{cos 10x}}$
$=$ R.H.S.
Hence proved.
17. Prove that:$\dfrac{\text{sin 5x+sin 3x}}{\text{cos 5x+cos 3x}}\text{=tan 4x}$
Ans:
We know that
$\text{sin A+sin B=2sin}\left( \dfrac{\text{A+B}}{\text{2}} \right)\text{cos}\left( \dfrac{\text{A-B}}{\text{2}} \right)\text{,}$
$\text{cos A+cos B=2cos}\left( \dfrac{\text{A+B}}{\text{2}} \right)\text{cos}\left( \dfrac{\text{A-B}}{\text{2}} \right)$
Now , L.H.S.$\text{=}\dfrac{\text{sin 5x+sin 3x}}{\text{cos 5x+cos 3x}}$
$\text{=}\dfrac{\text{2sin}\left( \dfrac{\text{5x+3x}}{\text{2}} \right)\text{cos}\left( \dfrac{\text{5x-3x}}{\text{2}} \right)}{\text{2cos}\left( \dfrac{\text{5x+3x}}{\text{2}} \right)\text{cos}\left( \dfrac{\text{5x-3x}}{\text{2}} \right)}$ (using the formula)
$\text{=}\dfrac{\text{2sin}\left( \dfrac{\text{5x+3x}}{\text{2}} \right)\text{cos}\left( \dfrac{\text{5x-3x}}{\text{2}} \right)}{\text{2cos}\left( \dfrac{\text{5x+3x}}{\text{2}} \right)\text{cos}\left( \dfrac{\text{5x-3x}}{\text{2}} \right)}$
$\text{=}\dfrac{\text{2sin 4x cos x}}{\text{2cos 4x cos x}}$
Further computing we have,
$\text{L}\text{.H}\text{.S=tan 4x}$
$=$ R.H.S.
18. Prove that \[\dfrac{\text{sin x-sin y}}{\text{cos x+cos y}}\text{=tan}\dfrac{\text{x-y}}{\text{2}}\]
Ans: We know that,
$\text{sin A-sin B=2cos}\left( \dfrac{\text{A+B}}{\text{2}} \right)\text{sin}\left( \dfrac{\text{A-B}}{\text{2}} \right)\text{,}$
.$\text{cos A+cos B=2cos}\left( \dfrac{\text{A+B}}{\text{2}} \right)\text{cos}\left( \dfrac{\text{A-B}}{\text{2}} \right)$
L.H.S.\[\text{=}\dfrac{\text{sin x-sin y}}{\text{cosx+cosy}}\]
$\text{=}\dfrac{\text{2cos}\left( \dfrac{\text{x+y}}{\text{2}} \right)\text{.sin}\left( \dfrac{\text{x-y}}{\text{2}} \right)}{\text{2cos}\left( \dfrac{\text{x+y}}{\text{2}} \right)\text{.cos}\left( \dfrac{\text{x-y}}{\text{2}} \right)}$
$\text{=}\dfrac{\text{sin}\left( \dfrac{\text{x-y}}{\text{2}} \right)}{\text{cos}\left( \dfrac{\text{x-y}}{\text{2}} \right)}$
$\text{=tan}\left( \dfrac{\text{x-y}}{\text{2}} \right)$
Therefore $\text{L}\text{.H}\text{.S=R}\text{.H}\text{.S}$
Hence proved.
19. Prove that $\dfrac{\text{sin x+sin 3x}}{\text{cos x+cos 3x}}\text{=tan 2x}$
Ans: We know that
$\text{sin A+sin B=2sin}\left( \dfrac{\text{A+B}}{\text{2}} \right)\text{cos}\left( \dfrac{\text{A+B}}{\text{2}} \right)\text{,}$
.\[\text{cos A+cos B=2cos}\left( \dfrac{\text{A+B}}{\text{2}} \right)\text{cos}\left( \dfrac{\text{A-B}}{\text{2}} \right)\]
Now , L.H.S.$\text{=}\dfrac{\text{sinx+sin3x}}{\text{cos x+cos 3x}}$
$\text{=}\dfrac{\text{2sin}\left( \dfrac{\text{x+3x}}{\text{2}} \right)\text{cos}\left( \dfrac{\text{x-3x}}{\text{2}} \right)}{\text{2cos}\left( \dfrac{\text{x+3x}}{\text{2}} \right)\text{cos}\left( \dfrac{\text{x-3x}}{\text{2}} \right)}$ (using the formula)
$\text{=}\dfrac{\text{sin 2x}}{\text{cos 2x}}$
$\text{=tan 2x}$
Therefore L.H.S$=$ R.H.S.
Hence proved.
20. Prove that $\dfrac{\text{sin x-sin 3x}}{\text{si}{{\text{n}}^{\text{2}}}\text{x-co}{{\text{s}}^{\text{2}}}\text{x}}\text{=2sin x}$
Ans: We know that,
$\text{sin A-sin B=2cos}\left( \dfrac{\text{A+B}}{\text{2}} \right)\text{sin}\left( \dfrac{\text{A-B}}{\text{2}} \right)$
And \[\text{co}{{\text{s}}^{\text{2}}}\text{A-si}{{\text{n}}^{\text{2}}}\text{A=cos 2A}\]
L.H.S.$\text{=}\dfrac{\text{sin x-sin 3x}}{\text{si}{{\text{n}}^{\text{2}}}\text{x-co}{{\text{s}}^{\text{2}}}\text{x}}$
\[\text{=}\dfrac{\text{2cos}\left( \dfrac{\text{x+3x}}{\text{2}} \right)\text{sin}\left( \dfrac{\text{x-3x}}{\text{2}} \right)}{\text{-cos2x}}\]
$\text{=}\dfrac{\text{2cos2xsin}\left( \text{-x} \right)}{\text{-cos 2x}}$
$\text{=-2 }\!\!\times\!\!\text{ }\left( \text{-sinx} \right)$
Therefore , we have,
$\text{L}\text{.H}\text{.S=2sin x}$
$=$ R.H.S.
Hence proved.
21. Prove that $\dfrac{\text{cos 4x+cos 3x+cos 2x}}{\text{sin 4x+sin 3x+sin 2x}}\text{=cot 3x}$
Ans: We know that,
$\text{cos A+cos B=2cos}\left( \dfrac{\text{A+B}}{\text{2}} \right)\text{cos}\left( \dfrac{\text{A-B}}{\text{2}} \right)$
And, $\text{sin A+sin B=2sin}\left( \dfrac{\text{A+B}}{\text{2}} \right)\text{cos}\left( \dfrac{\text{A-B}}{\text{2}} \right)$
Now, L.H.S.$\text{=}\dfrac{\text{cos 4x+cos 3x+cos 2x}}{\text{sin 4x+sin 3x+sin 2x}}$
\[\text{=}\dfrac{\left( \text{cos 4x+cos 2x} \right)\text{+cos 3x}}{\left( \text{sin4x+sin2x} \right)\text{+sin 3x}}\]
\[\text{=}\dfrac{\text{2cos}\left( \dfrac{\text{4x+2x}}{\text{2}} \right)\text{cos}\left( \dfrac{\text{4x-2x}}{\text{2}} \right)\text{+cos3x}}{\text{2sin}\left( \dfrac{\text{4x+2x}}{\text{2}} \right)\text{cos}\left( \dfrac{\text{4x-2x}}{\text{2}} \right)\text{+sin 3x}}\] (using the formulas)
\[\text{=}\dfrac{\text{2cos 3x cos x+cos 3x}}{\text{2sin 3x cos x+sin 3x}}\]
Further computing, we obtain,
L.H.S$\text{=}\dfrac{\text{cos 3x}\left( \text{2cos x+1} \right)}{\text{sin 3x}\left( \text{2cos x+1} \right)}$
\[\text{=cot 3x}\]
$=$ R.H.S.
Hence proved.
22. Prove that \[\text{cot x cot 2x-cot 2x cot 3x-cot 3x cot x=1}\]
Ans:
We know that, \[\text{cot}\left( \text{A+B} \right)\text{=}\dfrac{\text{cotAcotB-1}}{\text{cot A+cot B}}\]
Now , L.H.S.$\text{=cot xcot 2x-cot 2x cot 3x-cot 3x cot x}$
\[\text{=cot x cot 2x-cot 3x}\left( \text{cot 2x+cot x} \right)\]
\[\text{=cot x cot 2x-cot}\left( \text{2x+x} \right)\left( \text{cot 2x+cot x} \right)\]
\[\text{=cot x cot 2x-}\left[ \dfrac{\text{cot 2x cot x-1}}{\text{cot x+cot 2x}} \right]\left( \text{cot 2x+cot x} \right)\]
Further computing we obtain,
$\text{L}\text{.H}\text{.S=cot x cot 2x-}\left( \text{cot 2x cot x-1} \right)$
\[\text{=1}\]
$\text{=}$ R.H.S.
Hence proved.
23. Prove that $\text{tan 4x=}\dfrac{\text{4tan x}\left( \text{1-ta}{{\text{n}}^{\text{2}}}\text{x} \right)}{\text{1-6ta}{{\text{n}}^{\text{2}}}\text{x+ta}{{\text{n}}^{\text{4}}}\text{x}}$
Ans: We know that $\text{tan 2A=}\dfrac{\text{2tan A}}{\text{1-ta}{{\text{n}}^{\text{2}}}\text{A}}$
L.H.S.$\text{=tan 4x}$
$\text{=tan2}\left( \text{2x} \right)$
\[\text{=}\dfrac{\text{2tan 2x}}{\text{1-ta}{{\text{n}}^{\text{2}}}\left( \text{2x} \right)}\][using the formula]
$\text{=}\dfrac{\left( \dfrac{\text{4tan x}}{\text{1-ta}{{\text{n}}^{\text{2}}}\text{x}} \right)}{\left[ \text{1-}\dfrac{\text{4ta}{{\text{n}}^{\text{2}}}\text{x}}{{{\left( \text{1-ta}{{\text{n}}^{\text{2}}}\text{x} \right)}^{\text{2}}}} \right]}$
Further computing, we obtain,
L.H.S $\text{=}\dfrac{\left( \dfrac{\text{4tan x}}{\text{1-ta}{{\text{n}}^{\text{2}}}\text{x}} \right)}{\left[ \dfrac{{{\left( \text{1-ta}{{\text{n}}^{\text{2}}}\text{x} \right)}^{\text{2}}}\text{4ta}{{\text{n}}^{\text{2}}}\text{x}}{{{\left( \text{1-ta}{{\text{n}}^{\text{2}}}\text{x} \right)}^{\text{2}}}} \right]}$$$$$
$\text{=}\dfrac{\text{4tan x}\left( \text{1-ta}{{\text{n}}^{\text{2}}}\text{x} \right)}{\text{1+ta}{{\text{n}}^{\text{4}}}\text{x-2ta}{{\text{n}}^{\text{2}}}\text{x-4ta}{{\text{n}}^{\text{2}}}\text{x}}$
$\text{=}\dfrac{\text{4tan x}\left( \text{1-ta}{{\text{n}}^{\text{2}}}\text{x} \right)}{\text{1-6ta}{{\text{n}}^{\text{2}}}\text{x+ta}{{\text{n}}^{\text{4}}}\text{x}}$
$=$ R.H.S.
Hence proved.
24. Prove that $\text{cos 4x=1-8si}{{\text{n}}^{\text{2}}}\text{xco}{{\text{s}}^{\text{2}}}\text{x}$
Ans: We know that, $\text{cos 2x=1-2si}{{\text{n}}^{\text{2}}}\text{x}$
And $\text{sin 2x=2sin x cos x}$
L.H.S.\[\text{=cos 4x}\]
$\text{=cos 2}\left( \text{2x} \right)$
$\text{=1-2si}{{\text{n}}^{\text{2}}}\text{2x}$
$\text{=1-2}{{\left( \text{2sin x cos x} \right)}^{\text{2}}}$
Further computing we get,
L.H.S$\text{=1-8si}{{\text{n}}^{\text{2}}}\text{xco}{{\text{s}}^{\text{2}}}\text{x}$
$=$R.H.S.
Hence proved.
25. Prove that $\text{cos 6x=32xco}{{\text{s}}^{\text{6}}}\text{x-48co}{{\text{s}}^{\text{4}}}\text{x+18co}{{\text{s}}^{\text{2}}}\text{x-1}$
Ans: We know that, $\text{cos 3A=4co}{{\text{s}}^{\text{3}}}\text{A-3cosA}$
and $\text{cos 2x=1-2si}{{\text{n}}^{\text{2}}}\text{x}$
L.H.S.$\text{=cos 6x}$
$\text{=cos 3}\left( \text{2x} \right)$
\[\text{=4co}{{\text{s}}^{\text{3}}}\text{2x-3cos 2x}\]
\[\text{=4}\left[ {{\left( \text{2co}{{\text{s}}^{\text{2}}}\text{x-1} \right)}^{\text{3}}}\text{-3}\left( \text{2co}{{\text{s}}^{\text{2}}}\text{x-1} \right) \right]\]
Further computing,
L.H.S$\text{=4}\left[ {{\left( \text{2co}{{\text{s}}^{\text{2}}}\text{x} \right)}^{\text{3}}}\text{-}{{\left( \text{1} \right)}^{\text{3}}}\text{-3}\left( \text{2co}{{\text{s}}^{\text{2}}}\text{x} \right) \right]\text{-6co}{{\text{s}}^{\text{2}}}\text{x+3}$
$\text{=4}\left[ {{\left( \text{2co}{{\text{s}}^{\text{2}}}\text{x} \right)}^{\text{3}}}\text{-}{{\left( \text{1} \right)}^{\text{3}}}\text{-3}{{\left( \text{2co}{{\text{s}}^{\text{2}}}\text{x} \right)}^{\text{2}}}\text{+3}\left( \text{2co}{{\text{s}}^{\text{2}}}\text{x} \right) \right]\text{-6co}{{\text{s}}^{\text{2}}}\text{x+3}$
$\text{=4}\left[ \text{8co}{{\text{s}}^{\text{6}}}\text{x-1-12co}{{\text{s}}^{\text{4}}}\text{x+6co}{{\text{s}}^{\text{2}}}\text{x} \right]\text{-6co}{{\text{s}}^{\text{2}}}\text{x+3}$
$\text{=32co}{{\text{s}}^{\text{6}}}\text{x-48co}{{\text{s}}^{\text{4}}}\text{x+18co}{{\text{s}}^{\text{2}}}\text{x-1}$
Therefore we have,
L.H.S $=$ R.H.S.
Hence proved.
Miscellaneous Exercise
1. Prove that: $\text{2cos}\dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{13}}\text{cos}\dfrac{\text{9 }\!\!\pi\!\!\text{ }}{\text{13}}\text{+cos}\dfrac{\text{3 }\!\!\pi\!\!\text{ }}{\text{13}}\text{+cos}\dfrac{\text{5 }\!\!\pi\!\!\text{ }}{\text{13}}\text{=0}$
Ans: We know that $\text{cos x+cos y=2cos}\left( \dfrac{\text{x+y}}{\text{2}} \right)\text{cos}\left( \dfrac{\text{x-y}}{\text{2}} \right)$
Now L.H.S.$\text{=2cos}\dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{13}}\text{cos}\dfrac{\text{9 }\!\!\pi\!\!\text{ }}{\text{13}}\text{+cos}\dfrac{\text{3 }\!\!\pi\!\!\text{ }}{\text{13}}\text{+cos}\dfrac{\text{5 }\!\!\pi\!\!\text{ }}{\text{13}}$
$\text{=2cos}\dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{3}}\text{cos}\dfrac{\text{9 }\!\!\pi\!\!\text{ }}{\text{13}}\text{+2cos}\left( \dfrac{\dfrac{\text{3 }\!\!\pi\!\!\text{ }}{\text{13}}\text{+}\dfrac{\text{5 }\!\!\pi\!\!\text{ }}{\text{13}}}{\text{2}} \right)\text{cos}\left( \dfrac{\dfrac{\text{3 }\!\!\pi\!\!\text{ }}{\text{13}}\text{-}\dfrac{\text{5 }\!\!\pi\!\!\text{ }}{\text{13}}}{\text{2}} \right)$ (using the formula)
$\text{=2cos}\dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{13}}\text{cos}\dfrac{\text{9 }\!\!\pi\!\!\text{ }}{\text{13}}\text{+2cos}\dfrac{\text{4 }\!\!\pi\!\!\text{ }}{\text{13}}\text{cos}\left( \dfrac{\text{- }\!\!\pi\!\!\text{ }}{\text{13}} \right)$
$\text{=2cos}\dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{13}}\text{cos}\dfrac{\text{9 }\!\!\pi\!\!\text{ }}{\text{13}}\text{+2cos}\dfrac{\text{4 }\!\!\pi\!\!\text{ }}{\text{13}}\text{cos}\left( \dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{13}} \right)$
Simplifying,
$\text{L}\text{.H}\text{.S=2cos}\dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{13}}\left[ \text{cos}\dfrac{\text{9 }\!\!\pi\!\!\text{ }}{\text{13}}\text{+cos}\dfrac{\text{4 }\!\!\pi\!\!\text{ }}{\text{13}} \right]$
$\text{=2cos}\dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{13}}\left[ \text{2cos}\left( \dfrac{\dfrac{\text{9 }\!\!\pi\!\!\text{ }}{\text{13}}\text{+}\dfrac{\text{4 }\!\!\pi\!\!\text{ }}{\text{13}}}{\text{2}} \right)\text{cos}\dfrac{\dfrac{\text{9 }\!\!\pi\!\!\text{ }}{\text{13}}\text{-}\dfrac{\text{4 }\!\!\pi\!\!\text{ }}{\text{13}}}{\text{2}} \right]$
$\text{=2cos}\dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{13}}\left[ \text{2cos}\dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{2}}\text{cos}\dfrac{\text{5 }\!\!\pi\!\!\text{ }}{\text{26}} \right]$
Substituting $\text{cos}\dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{2}}\text{=0}$ , we get,
$\text{L}\text{.H}\text{.S=2cos}\dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{13}}\text{ }\!\!\times\!\!\text{ 2 }\!\!\times\!\!\text{ 0 }\!\!\times\!\!\text{ cos}\dfrac{\text{5 }\!\!\pi\!\!\text{ }}{\text{26}}$
$\text{=0}$
$=\text{R}\text{.H}\text{.S}$
Hence proved.
2. Prove that: $\left( \text{sin 3x+sin x} \right)\text{sin x+}\left( \text{cos 3x-cos x} \right)\text{cos x=0}$
Ans:
We know that, $\text{sin x+sin y=2sin}\left( \dfrac{\text{x+y}}{\text{2}} \right)\text{cos}\left( \dfrac{\text{x-y}}{\text{2}} \right)$
And $\text{cos x-cos y=-2sin}\left( \dfrac{\text{x+y}}{\text{2}} \right)\text{sin}\left( \dfrac{\text{x-y}}{\text{2}} \right)$
Now,
L.H.S.$\text{=}\left( \text{sin 3x+sin x} \right)\text{sin x+}\left( \text{cos 3x-cos x} \right)\text{cos x}$
$\text{=sin 3x sin x+si}{{\text{n}}^{\text{2}}}\text{x+cos 3x cos x-co}{{\text{s}}^{\text{2}}}\text{x}$ (using the formula)
$\text{=cos 3x cos x+sin 3x sin x-}\left( \text{co}{{\text{s}}^{\text{2}}}\text{x-si}{{\text{n}}^{\text{2}}}\text{x} \right)$
Simplifying we get,
$\text{L}\text{.H}\text{.S=cos}\left( \text{3x-x} \right)\text{-cos 2x}\,$
$\text{=cos 2x-cos 2x}$
$\text{=0}$
$=\text{R}\text{.H}\text{.S}\text{.}$
3. Prove that: ${{\left( \text{cos x+cos y} \right)}^{\text{2}}}\text{+}{{\left( \text{sin x-sin y} \right)}^{\text{2}}}\text{=4co}{{\text{s}}^{\text{2}}}\dfrac{\text{x+y}}{\text{2}}$
Ans: We know that, $\text{cos}\left( \text{x+y} \right)\text{=cos x cos y-sin xsin y}$
and L.H.S$\text{=}{{\left( \text{cos x+cos y} \right)}^{\text{2}}}\text{+}{{\left( \text{sin x-sin y} \right)}^{\text{2}}}$
\begin{align} & \text{=co}{{\text{s}}^{\text{2}}}\text{x+co}{{\text{s}}^{\text{2}}}\text{y+2cos x cos y+si}{{\text{n}}^{\text{2}}}\text{x+si}{{\text{n}}^{\text{2}}}\text{y-2sin x sin y} \\ & \\ \end{align}
$\text{=}\left( \text{co}{{\text{s}}^{\text{2}}}\text{x+si}{{\text{n}}^{\text{2}}}\text{x} \right)\text{+}\left( \text{co}{{\text{s}}^{\text{2}}}\text{y+si}{{\text{n}}^{\text{2}}}\text{y} \right)\text{+2}\left( \text{cos x cos y-sin x sin y} \right)$
Simplifying and using the formula,
L.H.S$\text{=1+1+2cos}\left( \text{x+y} \right)$
$\text{=2}\left[ \text{1+cos}\left( \text{x+y} \right) \right]$
$\text{=2}\left[ \text{1+2co}{{\text{s}}^{\text{2}}}\dfrac{\left( \text{x+y} \right)}{\text{2}}\text{-1} \right]$
[since $\text{2co}{{\text{s}}^{\text{2}}}\dfrac{\left( \text{x+y} \right)}{\text{2}}\text{-1=cos}\left( \text{x+y} \right)$ ]
$\text{=4co}{{\text{s}}^{\text{2}}}\left( \text{x+y} \right)$
Therefore L.H.S$=$ R.H.S
Hence proved.
4. Prove that: ${{\left( \text{cos x-cos y} \right)}^{\text{2}}}\text{+}{{\left( \text{sin x-sin y} \right)}^{\text{2}}}\text{=4si}{{\text{n}}^{\text{2}}}\dfrac{\text{x-y}}{\text{2}}$
Ans: We know that, $\text{cos}\left( \text{x-y} \right)\text{=cos x cos y+sin x sin y}$
L.H.S.$\text{=}{{\left( \text{cos x-cos y} \right)}^{\text{2}}}\text{+}{{\left( \text{sin x-sin y} \right)}^{\text{2}}}$
$\text{=co}{{\text{s}}^{\text{2}}}\text{x+co}{{\text{s}}^{\text{2}}}\text{y-2cos x cos y+si}{{\text{n}}^{\text{2}}}\text{x+si}{{\text{n}}^{\text{2}}}\text{y-2sin x sin y}$
\[\text{=}\left( \text{co}{{\text{s}}^{\text{2}}}\text{x+si}{{\text{n}}^{\text{2}}}\text{x} \right)\text{+}\left( \text{co}{{\text{s}}^{\text{2}}}\text{y+si}{{\text{n}}^{\text{2}}}\text{y} \right)\text{-2}\left[ \text{cos x cos y+sin x sin y} \right]\]
Simplifying and using the formula we get,
L.H.S $\text{=1+1-2}\left[ \text{cos}\left( \text{x-y} \right) \right]\,\,$
$\text{=2}\left[ \text{1-cos}\left( \text{x-y} \right) \right]$
$\text{=2}\left[ \text{1-}\left\{ \text{1-2si}{{\text{n}}^{\text{2}}}\left( \dfrac{\text{x-y}}{\text{2}} \right) \right\} \right]\,$
[since $\text{1-2si}{{\text{n}}^{\text{2}}}\dfrac{\left( \text{x-y} \right)}{\text{2}}\text{=cos}\left( \text{x-y} \right)$ ]
$\text{=4si}{{\text{n}}^{\text{2}}}\left( \dfrac{\text{x-y}}{\text{2}} \right)$
Therefore L.H.S$=$ R.H.S
Hence proved.
5. Prove that: $\text{sin x+sin 3x+sin 5x+sin 7x=4cos xcos 2xsin 4x}$
Ans: We know that $\text{sin A+sin B=2sin}\left( \dfrac{\text{A+B}}{\text{2}} \right)\text{.cos}\left( \dfrac{\text{A-B}}{\text{2}} \right)$
$\text{L}\text{.H}\text{.S}\text{. =sin x+sin 3x+sin 5x+sin 7x}$
\[\text{=}\left( \text{sin x+sin 5x} \right)\text{+}\left( \text{sin 3x+sin 7x} \right)\]
Using the formula and simplifying,
$\text{=2sin}\left( \dfrac{\text{x+5x}}{\text{2}} \right)\text{.cos}\left( \dfrac{\text{x-5x}}{\text{2}} \right)\text{+2sin}\left( \dfrac{\text{3x+7x}}{\text{2}} \right)\text{cos}\left( \dfrac{\text{3x-7x}}{\text{2}} \right)$
\[\text{=2cos 2x}\left[ \text{sin 3x+sin 5x} \right]\]
\[\text{=2cos 2x}\left[ \text{2sin}\left( \dfrac{\text{3x+5x}}{\text{2}} \right)\text{.cos}\left( \dfrac{\text{3x-5x}}{\text{2}} \right) \right]\]
\[\text{=2cos 2x}\left[ \text{2sin 4x}\text{.cos}\left( \text{-x} \right) \right]\]
Therefore we have,
\[\text{L}\text{.H}\text{.S=4cos 2x sin 4x cos x}\]
\[=\text{R}\text{.H}\text{.S}\]
6. Prove that: $\dfrac{\left( \text{sin 7x+sin 5x} \right)\text{+}\left( \text{sin 9x+sin 3x} \right)}{\left( \text{cos 7x+cos 5x} \right)\text{+}\left( \text{cos 9x+cos 3x} \right)}\text{=tan 6x}$
Ans: We known that,
$\text{sinA+sinB=2sin}\left( \dfrac{\text{A+B}}{\text{2}} \right)\text{.cos}\left( \dfrac{\text{A-B}}{\text{2}} \right)$
And $\text{cos A+cos B=2cos}\left( \dfrac{\text{A+B}}{\text{2}} \right)\text{.cos}\left( \dfrac{\text{A-B}}{\text{2}} \right)$
$\text{L}\text{.H}\text{.S}\text{. =}\dfrac{\left( \text{sin 7x+sin 5x} \right)\text{+}\left( \text{sin9x+sin3x} \right)}{\left( \text{cos 7x+cos 5x} \right)\text{+}\left( \text{cos9x+cos3x} \right)}$
Using the formula and simplifying,
$\text{=}\dfrac{\left[ \text{2sin}\left( \dfrac{\text{7x+5x}}{\text{2}} \right)\text{.cos}\left( \dfrac{\text{7x-5x}}{\text{2}} \right) \right]\text{+}\left[ \text{2sin}\left( \dfrac{\text{9x+3x}}{\text{2}} \right)\text{.cos}\left( \dfrac{\text{9x-3x}}{\text{2}} \right) \right]}{\left[ \text{2cos}\left( \dfrac{\text{7x+5x}}{\text{2}} \right)\text{.cos}\left( \dfrac{\text{7x-5x}}{\text{2}} \right) \right]\text{+}\left[ \text{2cos}\left( \dfrac{\text{9x+3x}}{\text{2}} \right)\text{.cos}\left( \dfrac{\text{9x-3x}}{\text{2}} \right) \right]}$
$\text{=}\dfrac{\left[ \text{2sin 6x}\text{.cos x} \right]\text{+}\left[ \text{2sin 6x}\text{.cos 3x} \right]}{\left[ \text{2cos 6x}\text{.cos x} \right]\text{+}\left[ \text{2cos 6x}\text{.cos 6x} \right]}$
$\text{=}\dfrac{\text{2sin 6x}\left[ \text{cos x+cos 3x} \right]}{\text{2cos 6x}\left[ \text{cos x+cos 3x} \right]}$
$\text{=tan 6x}$
Therefore L.H.S$=$ R.H.S
Hence proved.
7. Prove that:
$\text{sin 3x+sin 2x-sin x=4sin xcos}\dfrac{\text{x}}{\text{2}}\text{cos}\dfrac{\text{3x}}{\text{2}}$
Ans: We know that,
$\text{sin A+sin B=2sin}\left( \dfrac{\text{A+B}}{\text{2}} \right)\text{.cos}\left( \dfrac{\text{A-B}}{\text{2}} \right)$
And $\text{sin A-sin B=2sin}\left( \dfrac{\text{A-B}}{\text{2}} \right)\text{.cos}\left( \dfrac{\text{A+B}}{\text{2}} \right)$
$\text{L}\text{.H}\text{.S}\text{.=sin3x+sin2x-sinx}$
$\text{=sin 3x+}\left[ \text{2cos}\left( \dfrac{\text{2x+x}}{\text{2}} \right)\text{sin}\left( \dfrac{\text{2x-x}}{\text{2}} \right) \right]\,$
$\text{=sin 3x+}\left[ \text{2cos}\left( \dfrac{\text{3x}}{\text{2}} \right)\text{sin}\left( \dfrac{\text{x}}{\text{2}} \right) \right]$
Since we know that, $\text{sin 2x=2sin xcos x}$
$\text{L}\text{.H}\text{.S=2sin}\dfrac{\text{3x}}{\text{2}}\text{.cos}\dfrac{\text{3x}}{\text{2}}\text{+2cos}\dfrac{\text{3x}}{\text{2}}\text{sin}\dfrac{\text{x}}{\text{2}}\,\,\,\,\,\,$
$\text{=2cos}\left( \dfrac{\text{3x}}{\text{2}} \right)\left[ \text{sin}\left( \dfrac{\text{3x}}{\text{2}} \right)\text{+sin}\left( \dfrac{\text{x}}{\text{2}} \right) \right]$
\[\text{=2cos}\left( \dfrac{\text{3x}}{\text{2}} \right)\left[ \text{2sin}\left\{ \dfrac{\left( \dfrac{\text{3x}}{\text{2}} \right)\text{+}\left( \dfrac{\text{x}}{\text{2}} \right)}{\text{2}} \right\}\text{cos}\left\{ \dfrac{\left( \dfrac{\text{3x}}{\text{2}} \right)\text{-}\left( \dfrac{\text{x}}{\text{2}} \right)}{\text{2}} \right\} \right]\]
$\text{=2cos}\left( \dfrac{\text{3x}}{\text{2}} \right)\text{.2sin xcos}\left( \dfrac{\text{x}}{\text{2}} \right)$
Therefore
$\text{L}\text{.H}\text{.S=4sin xcos}\left( \dfrac{\text{x}}{\text{2}} \right)\text{cos}\left( \dfrac{\text{3x}}{\text{2}} \right)$
$\text{=R}\text{.H}\text{.S}$
8.Find $\text{sin}\dfrac{\text{x}}{\text{2}}\text{,cos}\dfrac{\text{x}}{\text{2}}$ and $\text{tan}\dfrac{\text{x}}{\text{2}}$ ,if $\text{tanx=-}\dfrac{\text{4}}{\text{3}}$ , $\text{x}$ lies in 2nd quadrant.
Ans: Here, $\text{x}$ is in 2nd quadrant.
Therefore ,
$\text{ }\dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{2}}\text{x }\!\!\pi\!\!\text{ }$
i.e, $\dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{4}}<\dfrac{\text{x}}{\text{2}}<\dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{2}}$
hence $\dfrac{\text{x}}{\text{2}}$ lies in 1st quadrant.
Therefore, \[\text{sin}\dfrac{\text{x}}{\text{2}}\text{,cos}\dfrac{\text{x}}{\text{2}}\,\,\,\] and $\text{tan}\dfrac{\text{x}}{\text{2}}$ are positive.
Given that $\text{tan x=-}\dfrac{\text{4}}{\text{3}}$
We know that, $\text{se}{{\text{c}}^{\text{2}}}\text{x=1+ta}{{\text{n}}^{\text{2}}}\text{x}$
$\text{se}{{\text{c}}^{\text{2}}}\text{x=1+ta}{{\text{n}}^{\text{2}}}\text{x}$
$\text{=1+}{{\left( \text{-}\dfrac{\text{4}}{\text{3}} \right)}^{\text{2}}}$
\[\text{=}\dfrac{\text{25}}{\text{9}}\]
As \[\text{x}\] is in 2nd quadrant, $\text{sec x}$ is negative.
Therefore , $\text{secx=-}\dfrac{\text{5}}{\text{3}}$
Then $\text{cos x=-}\dfrac{\text{3}}{\text{5}}$
Now we know that, $\text{2co}{{\text{s}}^{\text{2}}}\dfrac{\text{x}}{\text{2}}\text{=cos x+1}$
Computing we get, $\text{2co}{{\text{s}}^{\text{2}}}\dfrac{\text{x}}{\text{2}}\text{=}\dfrac{\text{2}}{\text{5}}$
Hence \[\text{cos}\dfrac{\text{x}}{\text{2}}\text{=}\dfrac{\text{1}}{\sqrt{\text{5}}}\]
Now we know that, $\text{si}{{\text{n}}^{\text{2}}}\text{x+co}{{\text{s}}^{\text{2}}}\text{x=1}$
Therefore substituting $\text{cos}\dfrac{\text{x}}{\text{2}}\text{=}\dfrac{\text{1}}{\sqrt{\text{5}}}$ and computing ,
$\text{sin}\dfrac{\text{x}}{\text{2}}\text{=}\dfrac{\text{2}}{\sqrt{\text{5}}}$
Hence ,
$\text{tan}\dfrac{\text{x}}{\text{2}}\text{=}\dfrac{\text{sin}\dfrac{\text{x}}{\text{2}}}{\text{cos}\dfrac{\text{x}}{\text{2}}}$
$=2$
Thus, the respective values of$\text{sin}\dfrac{\text{x}}{\text{2}}\text{,cos}\dfrac{\text{x}}{\text{2}}\,\text{,tan}\dfrac{\text{x}}{\text{2}}\,$
are $\,\dfrac{2\sqrt{5}}{5},\dfrac{\sqrt{5}}{5},\,\,2$ .
9.Find $\text{sin}\dfrac{\text{x}}{\text{2}}\text{,cos}\dfrac{\text{x}}{\text{2}}$ and $\text{tan}\dfrac{\text{x}}{\text{2}}$ ,if $\cos x\text{=-}\dfrac{1}{\text{3}}$ , $\text{x}$ lies in 3rd quadrant.
Ans: Here, $\text{x}$ is in 3rd quadrant.
Therefore ,
$\text{ }\!\!\pi\!\!\text{ x}\dfrac{\text{3 }\!\!\pi\!\!\text{ }}{\text{2}}$
i.e, $\dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{2}}\text{}\dfrac{\text{x}}{\text{2}}\text{}\dfrac{\text{3 }\!\!\pi\!\!\text{ }}{\text{4}}$
hence $\dfrac{\text{x}}{\text{2}}$ lies in 2nd quadrant.
Therefore, $\text{cos}\dfrac{\text{x}}{\text{2}}\,\,\,$ and $\text{tan}\dfrac{\text{x}}{\text{2}}$ are negative and $\text{sin}\dfrac{\text{x}}{\text{2}}$ is positive.
Given that $\text{cos x=-}\dfrac{1}{\text{3}}$
Now we know that, $\text{2co}{{\text{s}}^{\text{2}}}\dfrac{\text{x}}{\text{2}}\text{=cosx+1}$
Computing we get, $\text{2co}{{\text{s}}^{\text{2}}}\dfrac{\text{x}}{\text{2}}\text{=}\dfrac{\text{2}}{\text{3}}$
Hence $\text{cos}\dfrac{\text{x}}{\text{2}}\text{=-}\dfrac{\text{1}}{\sqrt{\text{3}}}$
Now we know that, $\text{si}{{\text{n}}^{\text{2}}}\text{x+co}{{\text{s}}^{\text{2}}}\text{x=1}$
Therefore substituting $\text{cos}\dfrac{\text{x}}{\text{2}}\text{=-}\dfrac{\text{1}}{\sqrt{\text{3}}}$ and computing ,
$\text{sin}\dfrac{\text{x}}{\text{2}}\text{=}\sqrt{\dfrac{\text{2}}{\text{3}}}$
Hence ,
$\text{tan}\dfrac{\text{x}}{\text{2}}\text{=}\dfrac{\text{sin}\dfrac{\text{x}}{\text{2}}}{\text{cos}\dfrac{\text{x}}{\text{2}}}$
$\text{=-}\sqrt{\text{2}}$
Thus, the respective values of $\text{sin}\dfrac{\text{x}}{\text{2}}\text{,cos}\dfrac{\text{x}}{\text{2}}\,\text{,tan}\dfrac{\text{x}}{\text{2}}\,$
are $\,\sqrt{\dfrac{\text{2}}{\text{3}}}\text{,-}\dfrac{\text{1}}{\sqrt{\text{3}}}\text{,}\,\text{-}\,\sqrt{\text{2}}$.
10.Find$\text{sin}\dfrac{\text{x}}{\text{2}}\text{,cos}\dfrac{\text{x}}{\text{2}}$ and $\text{tan}\dfrac{\text{x}}{\text{2}}$ ,if $\text{sin x=}\dfrac{1}{4}$ , $\text{x}$ lies in 2nd quadrant.
Ans: Here, $\text{x}$ lies in 2nd quadrant.
Therefore ,
$\text{ }\dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{2}}\text{x }\!\!\pi\!\!\text{ }$
i.e, $\dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{4}}<\dfrac{\text{x}}{\text{2}}<\dfrac{\text{ }\!\!\pi\!\!\text{ }}{\text{2}}$
hence $\dfrac{\text{x}}{\text{2}}$ lies in 1st quadrant.
Therefore, $\text{sin}\dfrac{\text{x}}{\text{2}}\text{,cos}\dfrac{\text{x}}{\text{2}}\,\,\,$ and $\text{tan}\dfrac{\text{x}}{\text{2}}$ are positive.
Given that $\text{sin x=}\dfrac{\text{1}}{\text{4}}$
Now we know that, $\text{si}{{\text{n}}^{\text{2}}}\text{x+co}{{\text{s}}^{\text{2}}}\text{x=1}$
Therefore substituting $\text{sin x=}\dfrac{\text{1}}{\text{4}}$ and computing ,
$\text{cos x=-}\dfrac{\sqrt{\text{15}}}{\text{4}}$
since $\text{x}$ lies in 2nd quadrant, $\text{cos x}$ is negative.
Now we know that, $\text{2si}{{\text{n}}^{\text{2}}}\dfrac{\text{x}}{\text{2}}\text{=1-cos x}$
Computing we get, $\text{2si}{{\text{n}}^{\text{2}}}\dfrac{\text{x}}{\text{2}}\text{=1+}\dfrac{\sqrt{\text{15}}}{\text{4}}$
Hence $\text{sin}\dfrac{\text{x}}{\text{2}}\text{=}\sqrt{\dfrac{\text{4+}\sqrt{\text{15}}}{\text{8}}}$
Now we know that, $\text{si}{{\text{n}}^{\text{2}}}\text{x+co}{{\text{s}}^{\text{2}}}\text{x=1}$
Therefore substituting $\text{sin}\dfrac{\text{x}}{\text{2}}\text{=}\sqrt{\dfrac{\text{4+}\sqrt{\text{15}}}{\text{8}}}$ and computing ,
$\text{cos}\dfrac{\text{x}}{\text{2}}\text{=}\sqrt{\dfrac{\text{4-}\sqrt{\text{15}}}{\text{8}}}$
Hence ,
$\text{tan}\dfrac{\text{x}}{\text{2}}\text{=}\dfrac{\text{sin}\dfrac{\text{x}}{\text{2}}}{\text{cos}\dfrac{\text{x}}{\text{2}}}$
$\text{=}\dfrac{\sqrt{\text{4+}\sqrt{\text{15}}}}{\sqrt{\text{4-}\sqrt{\text{15}}}}$
\[\text{=4+}\sqrt{\text{15}}\]
Thus, the respective values of $\text{sin}\dfrac{\text{x}}{\text{2}}\text{,cos}\dfrac{\text{x}}{\text{2}}\,\text{,tan}\dfrac{\text{x}}{\text{2}}\,$
are $\sqrt{\dfrac{\text{4+}\sqrt{\text{15}}}{\text{8}}}\text{,}\sqrt{\dfrac{\text{4-}\sqrt{\text{15}}}{\text{8}}}\text{,4+}\sqrt{\text{15}}$ .
NCERT Solutions for Class 11 Maths Chapter 3 Subtopics
Before wandering into the conceptual details of Trigonometric Functions Class 11, you can have a look at the summary of all topics discussed in this chapter.
Section 1: Introduction
In this part, students are introduced to fundamental trigonometric functions and their application. You will be required to perform calculations of distances based on these ratios.
Section 2: Angles
Class 11 Maths Trigonometry comes with four subsections under this topic. Students will learn about measurement of angles in different units, radians and degrees, and relations between them. Solutions to numerical sums involving the conversion of angle measurements from one form to another have been discussed in detail in NCERT Solutions for Class 11 Maths Chapter 3.
Section 3: Trigonometric Functions
This section deals with two topics. First one teaches the signs and symbols of generalised trigonometric functions in all four quadrants of a graph. In the next subsection, students will be acquainted with the domain and range of the different functions, that is, how the value of a function increases or decreases for an increasing angle value. You can find tables and detailed explanations on the working of these concepts in Trigonometric Functions Class 11 NCERT Solutions.
Section 4: Trigonometric Functions of Sum and Difference of Two Angles
The concluding section of Chapter 3 Maths Class 11 PDF focuses on the derivation of formulas and expressions based on trigonometric functions of the sums and differences between two angles. These formulas have been explained with the help of examples. Students must have a clear understanding of these as they make up an important part of geometric evaluations and are applied in a wide range of calculations.
Overview of Deleted Syllabus for CBSE Class 11 Maths Chapter - Trigonometric functions
Chapter | Dropped Topics |
Trigonometric Functions | 3.5 - Trigonometric Equations up to Exercise 3.4 |
Summary the last 5 points | |
3.6 -Proofs and Simple Applications of Sine and Cosine Formulae |
Class 11 Maths Chapter 3: Exercises Breakdown
Exercise | Number of Questions |
Exercise 3.1 | 7 Questions and Solutions |
Exercise 3.2 | 10 Questions and Solutions |
Exercise 3.3 | 25 Questions and Solutions |
Conclusion
The Class 11 Maths Ch 3 , "Trigonometric Functions," covers essential concepts including trigonometric ratios, identities, and equations. It is vital for understanding advanced mathematics. Typically, 2-3 questions from this chapter appear in exams, focusing on applications and problem-solving involving these functions.
By Understanding of this chapter lays a strong foundation for future topics in calculus and analytical geometry. Practising a variety of problems is crucial for success in this chapter and in subsequent mathematical studies.
Other Study Material for CBSE Class 11 Maths Chapter 3
Sr.No | Important Links for Chapter 3 Trigonometric Functions |
1 | |
2 | |
3 | |
4 | |
5 |
Chapter-Specific NCERT Solutions for Class 11 Maths 2025-26
Given below are the chapter-wise NCERT Solutions for Class 11 Maths. Go through these chapter-wise solutions to be thoroughly familiar with the concepts.
S. No | NCERT Solutions Class 11 Maths All Chapters |
1 | |
2 | |
3 | Chapter 4 - Complex Numbers and Quadratic Equations Solutions |
4 | |
5 | |
6 | |
7 | |
8 | |
9 | |
10 | Chapter 11 - Introduction to Three Dimensional Geometry Solutions |
11 | |
12 | |
13 |
Important Related Links for CBSE Class 11 Maths
S.No. | Important Study Material for Maths Class 11 |
1 | |
2 | |
3 | |
4 | |
5 | |
6 | |
7 | |
8 | |
9 | |
10 |
FAQs on NCERT Solutions For Class 11 Maths Chapter 3 Trigonometric Functions (2025-26)
1. Where can I find stepwise NCERT Solutions for Class 11 Maths Chapter 3 (Trigonometric Functions) as per the latest CBSE 2025–26 syllabus?
You can access detailed and stepwise NCERT Solutions for Class 11 Maths Chapter 3, Trigonometric Functions, in PDF format as per the latest CBSE 2025–26 syllabus directly on this page. All solutions are presented according to the official NCERT textbook pattern, ensuring complete alignment with in-chapter questions and exercises.
2. Are these the official NCERT answer keys for Class 11 Maths Chapter 3 exercises (3.1, 3.2, 3.3, and miscellaneous)?
All solutions provided here are prepared strictly as per the NCERT textbook and CBSE-approved methods for Class 11 Maths Chapter 3. The answers follow the latest NCERT answer format, including stepwise solutions for exercises 3.1, 3.2, 3.3, and the miscellaneous section, ensuring suitability for 2025–26 CBSE board preparations.
3. How do I solve Exercise 3.3 of Class 11 Maths Chapter 3 using the textbook method?
To solve Exercise 3.3 of Class 11 Maths Chapter 3, first refer directly to the relevant NCERT exercise in your textbook. Each solution here provides a stepwise explanation starting from identifying the trigonometric identities required, applying them according to NCERT pattern, and justifying each transformation until the final answer matches the CBSE-expected format.
4. Can I download NCERT Solutions for Class 11 Maths Chapter 3, including all exercises, as a single PDF?
Yes, you can easily download the complete NCERT Solutions for Class 11 Maths Chapter 3 in PDF format covering all exercises (3.1, 3.2, 3.3, and Miscellaneous). The PDF contains CBSE 2025–26 approved stepwise answers, formatted as per latest NCERT guidelines for hassle-free offline study.
5. Are the answers for intext (within-chapter) and back exercises of Trigonometric Functions provided in the same CBSE pattern?
Yes, all answers for both intext and back exercises of Class 11 Maths Chapter 3 are solved using the same NCERT-authorized stepwise approach and CBSE answer writing pattern. This ensures that each solution, whether for a within-chapter or end-of-chapter question, is presented in the official format for maximum scoring.
6. What is the correct method to simplify trigonometric identities in Chapter 3, as per NCERT pattern?
For simplifying trigonometric identities in Class 11 Maths Chapter 3, always start by writing the given expression and identifying suitable NCERT-approved identities. Apply these stepwise, showing each substitution and simplification, until the required answer is obtained, as demonstrated in the official NCERT solutions here.
7. Is there a Hindi medium version of Class 11 Maths Chapter 3 NCERT Solutions available?
Yes, NCERT Solutions for Class 11 Maths Chapter 3 (Trigonometric Functions) are also available in Hindi medium, following the exact same CBSE 2025–26 syllabus and solution pattern. Students studying in Hindi medium can download the stepwise solved answers in PDF for each exercise.
8. Which chapter covers Trigonometric Functions in Class 11 Maths NCERT?
Trigonometric Functions are covered in Chapter 3 of the Class 11 NCERT Mathematics textbook. All exercise and miscellaneous solutions provided here strictly follow the structure, sequence, and level of the official NCERT Chapter 3.
9. How can I ensure my answers match the CBSE marking scheme for Chapter 3 Trigonometry?
To ensure your answers align with the CBSE marking scheme, follow the stepwise NCERT answer format shown here: start from the question, use only Board-approved trigonometric identities, show all working in logical order, and conclude with a clearly boxed final answer, mirroring the solutions in this NCERT Solutions set.
10. What are the benefits of using stepwise NCERT Solutions for Class 11 Maths Chapter 3 while preparing for exams?
Using stepwise NCERT Solutions for Class 11 Maths Chapter 3 helps you understand the logic behind every step, reduces calculation errors, and ensures answers are written as per CBSE expectations. This structured approach is key for scoring full marks in both board and class tests, as it mirrors the CBSE answer key style.
11. How to score full in Maths Class 11, especially in Chapter 3 Trigonometric Functions?
Scoring full in Class 11 Maths, particularly in Chapter 3, requires consistent practice of stepwise NCERT solutions, understanding each identity and formula, and writing answers exactly in the CBSE format. Start with the NCERT pattern for solved questions and review your approach using the official answer formats shown here for maximum accuracy.
12. Is Class 11 Maths difficult, and how do official NCERT Solutions help with tough chapters like Trigonometric Functions?
Many students find Class 11 Maths challenging due to advanced topics like Trigonometric Functions. Accessing official NCERT Solutions provides you with detailed, stepwise methods for all exercises, simplifies tough problems using the prescribed format, and builds strong conceptual clarity as expected by CBSE guidelines.
13. Which chapters in Class 11 Maths are considered the toughest, and where does Chapter 3 rank?
Chapters like Trigonometric Functions (Chapter 3), Coordinate Geometry, and Permutations & Combinations are often considered among the toughest in Class 11 Maths. Chapter 3 is regarded as challenging due to the variety of identities and transformations involved, making clear stepwise NCERT solutions essential for mastering the concepts.
14. Are the Miscellaneous Exercise questions of Chapter 3 solved using the same NCERT method?
Yes, every miscellaneous exercise question of Class 11 Maths Chapter 3 is solved using the stepwise NCERT method, demonstrating all the required trigonometric identities and reasoning in a clear sequence that matches the expected CBSE answer format for 2025–26.
15. Do I need to show all steps as in the NCERT answer format in my final board exams for Chapter 3?
Yes, for full marks in CBSE board or school exams, it’s mandatory to show all essential steps as per the NCERT answer format, especially while solving Trigonometric Functions in Chapter 3. Each step must be logically presented, as modeled in the solutions above, to ensure the examiner can follow your reasoning and award complete marks.

























