




Trigonometric Function: An Introduction
Sine, cosine, tangent, cosecant, secant, and cotangent are the six trigonometric functions. There are numerous identities involving these six trigonometric functions that are used to solve many mathematical problems, and they are all related to one another in some way.
Sine, cosine, and tangent are the three fundamental among them because we can derive the other three using these fundamental functions. Secant is the reciprocal of cosine, cotangent is the reciprocal of a tangent, and cosecant is the reciprocal of sine. While tangent and cotangent have a periodicity of $\pi$, sine, cosine, secant, and cosecant have a periodicity of $2\pi$.
What is the Value of tan 180?
In Trigonometry, the measurement of tan 180 degrees equals 0. The \[\tan{180}^{\circ}\] can also be represented by 3.14159, which is the spherical geometry equivalent to the specific angle of 180 degrees.
How to Calculate Tan Value at 180 Degrees?
In this section, we will learn methods to find the value \[\tan{180}^{\circ}\].
The method for determining $\tan 180$ degree is as follows:
Making Use of Trigonometric Functions
Using Unit Circle
Value of Tan 180 Degrees Using Unit Circle
The \[\tan{180}^{\circ}\] can be expressed as $\tan \pi$ in a circular notation.
We already know that the tan can be written as \[\dfrac{\text{sin}}{\text{cos}}\]. The tan 180 value can be obtained from the unit circle using this relationship.
We can calculate the tangent values for each degree for a unit circle with a radius of 1. We can determine all the trigonometric ratios and values by using a unit circle drawn on the XY plane.
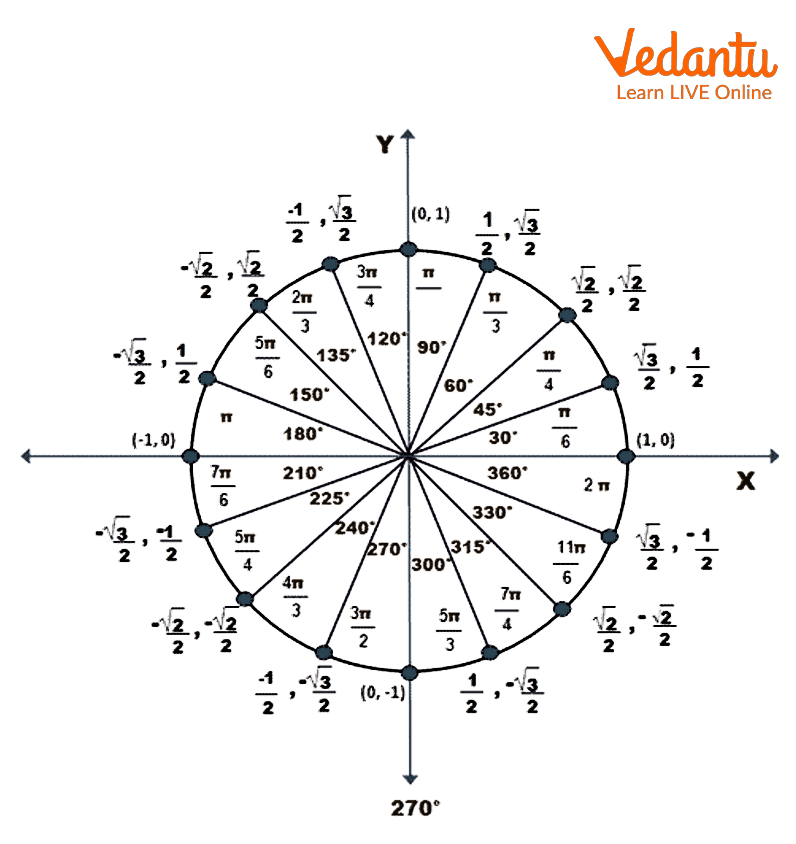
Value of Tan 180 Degrees on the Unit Circle
We know,
\[\sin 180^0=0\] and \[\cos 180^0 = -1\]
Therefore, \[\tan 180^0 = \dfrac{\sin 180^0}{\cos 180^0}\]
$=\dfrac{0}{-1}=0$
Value of Tan 180 Degrees Using Trigonometric Functions
In trigonometric ratios of angles \[(180\cos 180^{\circ}- \theta)\], we will find the relation between all six trigonometric ratios.
We know that
\[\sin (90^0 + \theta) = \cos \theta\]
\[\cos (90^0 + \theta) = - \sin \theta\]
\[\tan (90^0 + \theta) = - \cot \theta\]
\[\csc (90^0 + \theta) = \sec \theta\]
\[\sec ( 90^0 + \theta) = - \csc \theta\]
\[\cot ( 90^0 + \theta) = - \tan \theta\]
and
\[\sin (90^0 - \theta) = \cos \theta\]
\[\cos (90^0 - \theta) = \sin \theta\]
\[\tan (90^0 - \theta) = \cot \theta\]
\[\csc (90^0 - \theta) = \sec \theta\]
\[\sec (90^0 - \theta) = \csc \theta\]
\[\cot (90^0 - \theta) = \tan \theta\]
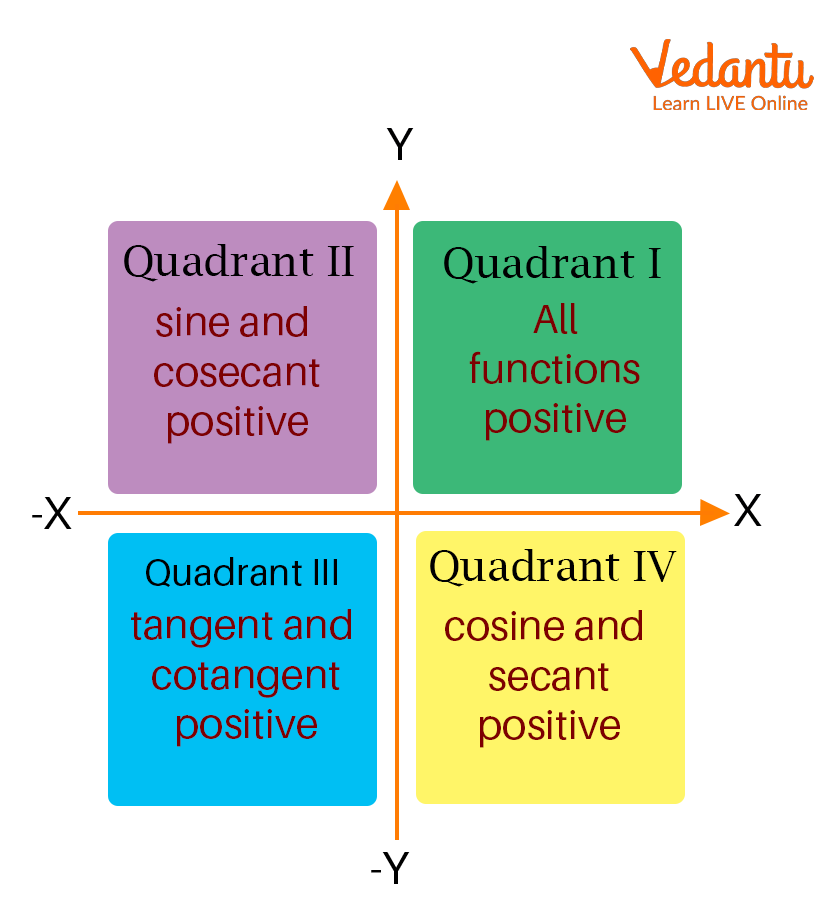
Trigonometric Ratios in Quadrants
Now, \[180^0\] can be mathematically defined as \[tan(90^0 + 90^0)\].
According to the above image, \[tan(90^0 + A)\] is located in the second quadrant, so the tan is positive.
\[= – \cot 90^0\]
\[= –\dfrac{(\cos 90^0)} { \sin 90^0)}\]
\[= – \dfrac{0}{1}\]
\[= 0\]
Consequently, \[\tan 180^0 = 0\]
Alternately, \[\tan 180^0\] can be calculated as:
\[\tan 180^0 = \tan(180^0 – 0) = – \tan 0^0 = 0\]
Solved Examples
Example 1: Find the value of tan 1200.
Solution: \[\tan 120^0 = \tan(180^0 – 60^0)\]
\[= –\ tan 60^0\]
$= – \sqrt{3}$
So, the value of $\tan 120^0$ is $-\sqrt{3}$
Example 2: Evaluate 2tan1800 - tan1500.
Solution: \[2 \tan180^0 - \tan150^0\]
\[= 2\ tan 180^0 - \tan(180^0 -30^0\]
\[= 2(0) - (-\tan 30^0)\]
\[= 0 + \tan 30^0\]
\[= \dfrac{1}{\sqrt{3}}\]
So, the value of $2\tan180^0 – \tan150^0$ is $= \dfrac{1}{\sqrt{3}}$
Example 3: Find tan1800 + cot 450.
Solution: The value of \[\tan 180^0 = 0\] and \[\cot 45^0 = 1\].
Therefore,
\[\tan 180^0 + \cot 45^0\]
$= 0 + 1 = 1$
So, the value of $\tan 180^0 + \cot 45^0$ is 1.
Example 4: Find the value of tan2400.
Solution: \[\tan 240^0= tan (180 + 60)^0\]
\[= tan 60^0\]
We know \[\tan (180^{\circ} + \theta) = tan \theta\]
$ = \sqrt{3}$
So, the value of $\tan 240^0$ is $ = \sqrt{3}$
Practice Problem
Q 1. Find sec 1500.
Q 2. Find tan 1200 + cot 450.
Answer
$\dfrac{-2}{\sqrt{3}}$
$1-\sqrt{3}$
Conclusion
To summarise, the measurement of tan 180 degrees equals 0. $\tan 180 °$ can also be represented by 3.14159, which is the spherical geometry equivalent to the specific angle of 180 degrees. The cot of an angle is the reciprocal of a tan. We hope this article helped you understand how to find the value of $\tan 180$ degrees. Take out a pencil and piece of paper and try to practise the questions given above in this article by yourself.
FAQs on Value of Tan 180
1. What is the exact value of tan 180° in trigonometry?
The exact value of the tangent of 180 degrees (tan 180°) is 0. This is a fundamental value for an angle located on the negative x-axis in the Cartesian coordinate system.
2. What are the main methods to determine the value of tan 180°?
There are two primary methods to find the value of tan 180° as per the NCERT syllabus for the 2025-26 session:
- Using the Unit Circle: By identifying the coordinates of the point on the unit circle corresponding to 180°, which are (-1, 0).
- Using Trigonometric Identities: By expressing tan 180° as a ratio of sin 180° and cos 180°, or by using allied angle formulas like tan(90° + 90°) or tan(180° - 0°).
3. Why is the value of tan 180° equal to zero and not undefined?
The value of tan 180° is zero because the tangent function is defined as the ratio of sine to cosine (tan θ = sin θ / cos θ). At 180 degrees:
- The value of sin 180° is 0.
- The value of cos 180° is -1.
Therefore, tan 180° = sin 180° / cos 180° = 0 / -1 = 0. The result is a defined number, zero, because the denominator is not zero.
4. How do the values of sin 180°, cos 180°, and tan 180° relate to each other on the unit circle?
On a unit circle (a circle with a radius of 1), any point on its circumference has coordinates (cos θ, sin θ). For an angle of 180°, the point lies on the negative x-axis. Thus, its coordinates are (-1, 0). This directly gives us:
- cos 180° = x-coordinate = -1
- sin 180° = y-coordinate = 0
- tan 180° = y/x = 0 / -1 = 0
This geometric representation clarifies why each function has its specific value at 180°.
5. What is the importance of the identity tan(180° + θ) = tan θ?
The identity tan(180° + θ) = tan θ is important because it demonstrates the periodicity of the tangent function. It shows that the value of the tangent function repeats every 180° (or π radians). This property is crucial for solving trigonometric equations and understanding the graph of the tangent function, which has vertical asymptotes and repeating cycles.
6. Why is tan 180° zero, while its reciprocal, cot 180°, is undefined?
This difference is a key example of how reciprocal trigonometric functions behave. While tan 180° = sin 180° / cos 180° = 0 / -1 = 0, its reciprocal function, cotangent, is calculated as:
cot 180° = cos 180° / sin 180° = -1 / 0
Since division by zero is mathematically undefined, the value of cot 180° is undefined. This highlights a critical distinction between the two functions at this specific angle.
7. How is the formula for tan(180° - θ) used in solving problems?
The formula tan(180° - θ) = -tan θ is used to find the tangent of obtuse angles by relating them to acute angles. For example, to find the value of tan 120°, we can express it as:
tan 120° = tan(180° - 60°)
Using the formula, this becomes -tan 60°, which is equal to -√3. This method simplifies calculations for angles in the second quadrant.
8. Can you provide an example of a calculation where knowing the value of tan 180° is essential?
Certainly. Consider the problem of evaluating the expression: 2 tan 180° + 3 cos 180°.
To solve this, you must know the specific values:
- tan 180° = 0
- cos 180° = -1
Substituting these values into the expression gives:
2(0) + 3(-1) = 0 - 3 = -3. Without knowing that tan 180° is exactly zero, the problem cannot be solved correctly.









