




How Do Unequal Parts Differ from Equal Parts?
Have you tried to divide anything into parts? This can be to distribute something among your friends or to take one part out and leave the rest of the parts to have later. How do you prefer to divide these parts? The general answer is “equally”. However, any object or item can also be divided into parts that are not equal in shape, size, or any other proportion. Not always do we get to deal with equal portions of an object or a number, so it is important that we know how unequal parts work. Let us learn more about this idea.
Definition of Unequal Parts
When trying to divide a whole into two or more parts, if the parts do not match each other in proportion or any other aspect, the parts are said to be unequal parts. Let us consider a few examples to understand the concept better.
Examples of Unequal Parts of a Whole
Let us consider the following image for understanding the idea of unequal parts clearly. The following image is a pie diagram that represents three different parts that a whole is divided into. The three parts are coloured green, blue, and red, respectively.
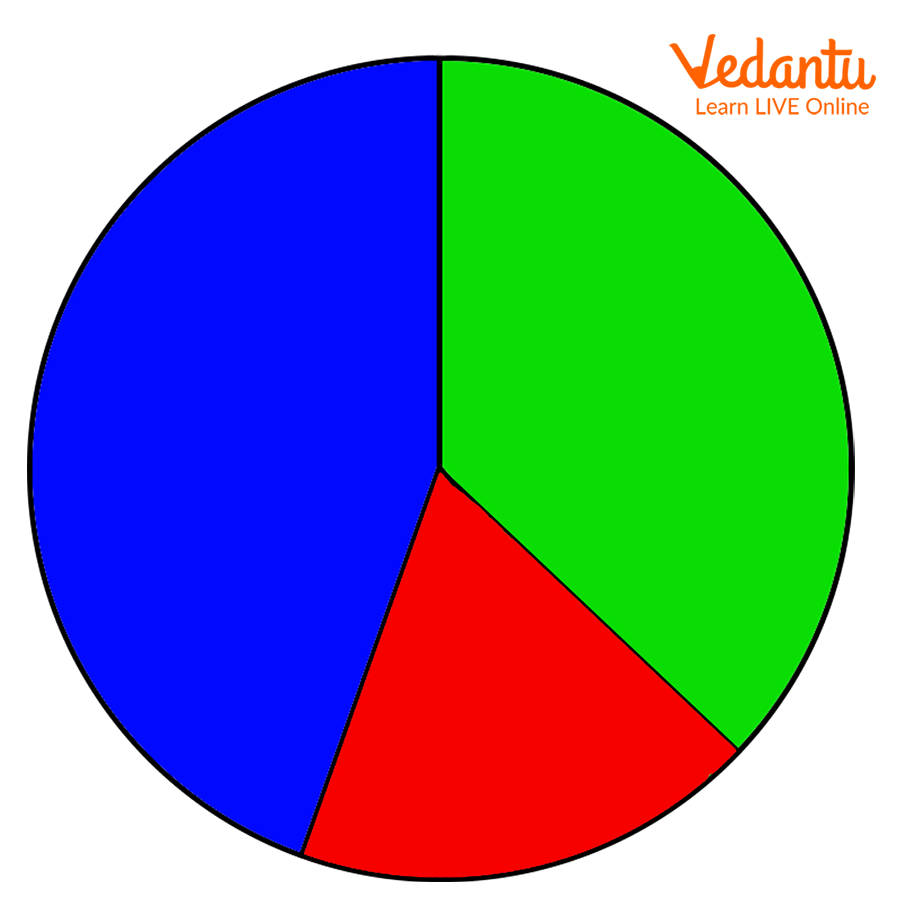
A Pie Diagram Representing Three Unequal Parts Coloured Green, Blue, and Red, Respectively
From the given diagram, we can observe that the whole is divided into three parts that are not equal in proportion, that is, the green part is not equal to the blue part or the red part, and the blue part is not equal to the red part or the green part, and the red part is not equal to the green part or the blue part. So, these three parts can be called unequal parts of a whole.
Now, let us take this concept to a Mathematical level. Suppose there is a pie that needs to be divided into 5 equal parts. Then each portion of the pie will be represented in fractional notation as ⅕. However, if we were to divide the same pie into 5 unequal parts, then an option would be to divide it into the parts 1/15, 2/15, 3/15, 4/15, and 5/15. All these 5 parts are unequal and, when added together, give a whole. So, this was a Mathematical example of unequal parts.

A Pie Divided into 5 Unequal Parts
Conclusion
Unequal parts of an object or number are those parts that together form a whole but are not equal to each other in proportion of size, shape, or any other aspect. Equal parts are easy to deal with in Maths, but unequal parts are equally important and should not be left out. The concept should be understood properly to be able to solve problems based on unequal parts.
FAQs on Mastering Unequal Parts: Meaning, Diagrams & Practice
1. What are unequal parts in Maths?
In Maths, unequal parts are pieces of a whole object or group that are not the same in size, quantity, or value. For example, if you break a biscuit into one big piece and one small piece, you have created unequal parts of the whole biscuit.
2. Can you give some examples of unequal parts?
Yes, unequal parts are common in daily life. Here are a few examples:
Cutting a pizza where one person gets a much larger slice than everyone else.
Sharing 10 candies between two friends as 7 and 3.
A rope cut into two pieces where one is visibly longer than the other.
A book with chapters of different lengths (some long, some short).
3. How can you tell the difference between equal parts and unequal parts?
The main difference is the size or amount of each part. You can tell them apart by checking if all the pieces are identical.
Equal parts: All the pieces of the whole are of the exact same size. Think of a standard chocolate bar with squares that are all identical.
Unequal parts: The pieces are of different sizes. If you randomly break a cookie, the resulting pieces will most likely be unequal.
4. Why is it important to understand the concept of unequal parts?
Understanding unequal parts is a very important real-world skill. It helps us identify situations that are not divided fairly. It also forms the basic idea needed for more advanced math topics, like working with fractions that have different denominators. In everyday life, from sharing resources to managing time, things are rarely divided perfectly equally, so knowing how to compare unequal amounts is crucial for problem-solving.
5. Where can we find examples of unequal parts in everyday life?
We see unequal parts everywhere. For instance, when you divide your study time, you might spend 1 hour on Maths and 30 minutes on English; these are unequal time periods. When a pizza is shared among people with different appetites, the slices are often cut into unequal sizes. Even the continents on Earth are unequal parts of the world's total landmass.
6. If you join two unequal parts, can they still form a complete whole?
Yes, absolutely. The term 'unequal' only describes how a whole was divided. When you put all the unequal parts back together without any gaps or overlaps, they will perfectly re-form the original whole object. For instance, if a wooden plank is cut into a long piece and a short piece, putting them end-to-end gives you back the complete plank. The whole is simply the sum of all its parts, whether they are equal or unequal.
7. How does the idea of unequal parts relate to fractions?
This is a key concept for learning fractions correctly as per the CBSE syllabus. A fundamental rule of basic fractions (like 1/2, 1/3, or 1/4) is that they must represent equal parts of a whole. If you cut a cake into three unequal slices, you cannot call any single slice 'one-third' (1/3) of the cake. Understanding this difference helps prevent common mistakes when students begin learning about fractions.









