Thales’s Theorem Explained: Definition & Application in Triangles

Thales’s Theorem is also known as Basic Proportionality Theorem or Side splitter Theorem. It was introduced by a famous Greek mathematician, Thales. Hence, it is called the Thales Theorem. Thales’s Theorem is an important tool of elementary geometry and helps us in solving problems related to triangles. Also, this concept has been introduced in the Similar Triangles. The applications of Thales's Theorem, limitations, and Thales’s Theorem examples will be discussed here in detail for a clear understanding of the theorem. So, let us discuss the theorem.

History of Mathematician

Thales of Miletus

Name: Thales of Miletus

Born: 624 BC

Died: 548 B

Field: Mathematics

Nationality: Greek

Thales Theorem Statement

When a line is drawn parallel to a side of a triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio.

Thales Theorem Proof

Proof of Thales's Theorem

Consider a triangle $A B C$. In the triangle, a line parallel to side $B C$ is drawn which intersects the other two sides $A B$ and $A C$ at $D$ and $E$, respectively, as shown in the above diagram.

To prove: $\dfrac{A D}{D B}=\dfrac{A E}{E C}$.
Construction: Join $B E$ and $C D$ and then draw $D M \perp A C$ and $E N \perp A B$.

So, the area of $\triangle A D E\left(=\dfrac{1}{2}\right.$ base $\times$ height $)=\dfrac{1}{2} A D \times E N$.

So, $\operatorname{ar}(A D E)=\dfrac{1}{2} A D \times E N$, where $\operatorname{ar}(A D E)$ denotes the area of the triangle.

Similarly, $\operatorname{ar}(B D E)=\dfrac{1}{2} D B \times E N$,

$\operatorname{ar}(A D E)=\dfrac{1}{2} A E \times D M$, and

$\operatorname{ar}(D E C)=\dfrac{1}{2} E C \times D M$

$\dfrac{\operatorname{ar}(A D E)}{\operatorname{ar}(B D E)}=\dfrac{\dfrac{1}{2} A D \times E N}{\dfrac{1}{2} D B \times E N}=\dfrac{A D}{D B}$

Also,

$\dfrac{\operatorname{ar}(A D E)}{\operatorname{ar}(D E C)}=\dfrac{\dfrac{1}{2} A E \times D M}{\dfrac{1}{2} E C \times D M}=\dfrac{A E}{E C}$

We can note that $\triangle B D E$ and $\triangle D E C$ are on the same base $D E$ and between the same parallel lines $B C$ and $D E$.

So,

$\operatorname{ar}(B D E)=\operatorname{ar}(D E C)$

So, from the above equations, we have

$\dfrac{A D}{D B}=\dfrac{A E}{E C}$

Hence, the proof of Thales's Theorem.

Limitations of Thales Theorem

• Thales's theorem is applicable if the line drawn is parallel and doesn't tell anything if the drawn line is not a parallel line to the third side.

Applications of Thales Theorem

• Thales's Theorem is used in tiles and also used in making paintings.

• Thales's Theorem is used to find the length of the triangle if the ratio in which the sides are divided is given.

• Thales's theorem is applicable to all types of triangles.

Thales Theorem Examples

1. Suppose $A B C$ is a triangle, where $D E$ is a line that is drawn from the midpoint of $A B$ and ends midpoint of $A C$ at $E \cdot \dfrac{A D}{D B}=\dfrac{A E}{E C}$ and $\angle A D E=\angle A C B$. Then prove that triangle $A B C$ is an isosceles triangle.

Solution:

Given, $\dfrac{A D}{D B}=\dfrac{A E}{E C}$.

Using the converse of the basic proportionality theorem (Thales's theorem), we have $D E \| B C$

But we are given,

$\Rightarrow \angle A D E=\angle A C B$

So,

$\Rightarrow \angle A B C=\angle A C B$

The sides opposite to the equal angles are also equal.

$\Rightarrow A B=A C$

So, $A B C$ is an isosceles triangle.

2. In the given figure $D E \| B C$. If $A D=x, D B=x-3, A E=x+3$, and $E C=x-1$, find the value of $x$.

Triangle ABC

Solution:

In $\triangle A B C, D E \| B C$.

$\Rightarrow \dfrac{A D}{D B}=\dfrac{A E}{E C}$

(Using basic Thales's theorem)

$\Rightarrow \dfrac{x}{x-2}=\dfrac{x+2}{x-1}$

$\Rightarrow x(x-1)=(x+3)(x-3)$

$\Rightarrow x^{2}-x=x^{2}-9$

$\Rightarrow x=9$

3. $D$ and $E$ are, respectively, the points on the sides $A B$ and $A C$ of a $\triangle A B C$ such that $A B=5.6 \mathrm{~cm}, A D=1.4 \mathrm{~cm}, A C=7.2 \mathrm{~cm}$, and $A E=1.8 \mathrm{~cm}$. Show that $D E \| B C$.

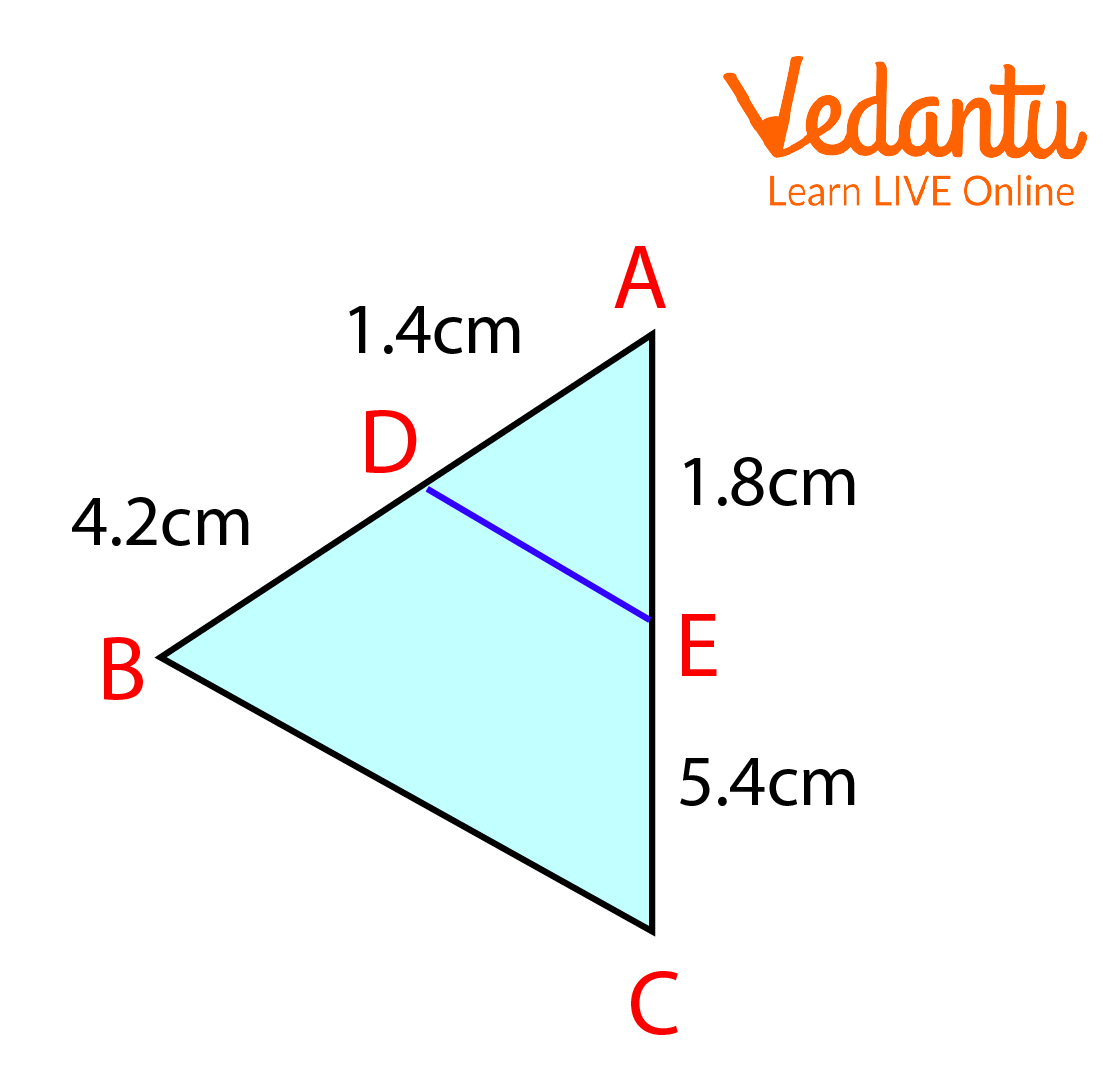
ABC is a Triangle

Solution:

We have $A B=5.6 \mathrm{~cm}, A D=1.4 \mathrm{~cm}, A C=7.2 \mathrm{~cm}$, and $A E=1.8 \mathrm{~cm}$.

$B D=A B-A D=5.6-1.4=4.2 \mathrm{~cm}$

and $E C=A C-A E=7.2-1.8=5.4 \mathrm{~cm}$

$\Rightarrow \dfrac{A D}{D B}=\dfrac{1.4}{4.2}=\dfrac{1}{3}$

and

$\Rightarrow \dfrac{A E}{E C}=\dfrac{1.8}{5.4}=\dfrac{1}{3}$

$\Rightarrow \dfrac{A D}{D B}=\dfrac{A E}{E C}$

Hence, using the converse of Thales's Theorem, we can say that

$D E$ is parallel to $B C$.

Conclusion

In the article, we have discussed Thales's Theorem and the proof of Thales's Theorem. We have also solved some questions related to the theorem. Thales's Theorem has a wide range of applications in real life also and is an important part of geometry. So, Thales's theorem is a very important theorem and reduces mathematical work related to triangles.

Important Points to Remember

A line drawn parallel to the third side of the triangle divides the other two sides of the triangle in equal ratio.

Important Formulas to Remember

Thales Theorem formula: If $ABC$ is a triangle and a line parallel to side $BC$ is drawn which intersects the other two sides $AB$ and $AC$ at $D$ and $E$, respectively, then,

$\dfrac{A D}{D B}=\dfrac{A E}{E C}$