




How Radians Connect to Real Numbers: Definitions, Uses & Examples
We usually use the radian and degrees as units to measure an angle. The relation between radians and degrees is the relationship between radians and real numbers because the degree is a real number. Radian is used to measure the arc of a circle and is easy to calculate. The real number of a radian is not a whole number but is easy to visualize on the number line.
What is a radian?
The radian is an S.I. unit used to measure angles and the radian is the angle that an arc whose length is equal to the radius of a circle forms at the center of the circle. One radian, shown directly below, equals approximately 57.296 degrees. Use radians instead of degrees when calculating angles as radii. Since ‘°’ is used to represent degrees, rad or c is used to represent radians. For example, 1.5 radians is written as 1.5 radians or 1.5 c.
The Radian of a Number System
Radian of a number system is known as the number of counting digits in a number system. For example, decimal number system has 10 digits, i.e., 0, 1, 2, …, 9. Thus the radian of decimal system is 10. Similarly Binary number system has a radian 2, octal has 8 and hexadecimal has 16.
Relation between Radian and Real Numbers
The circumference of a circle is \[2\pi r\], where r is the radius of the circle. The arc length of a circle with a radius of 1 unit is \[2\pi \] radian. Again we know that \[2\pi \] radian = 360.
Divide both sides by \[2\pi \]
\[1\,radian = \dfrac{{360}}{{2\pi }}\]
Putting the \[\pi = \dfrac{{22}}{7}\]
\[1\,radian = \dfrac{{360}}{{2 \times \dfrac{{22}}{7}}}\]
Solving the above equation:
\[1\,radian = 57.296\]
By solving the equation we get 1 radian = 57.296. The relationship between radian and real numbers is 1 radian = 57.296(approx.).
What is the relationship between radians and real numbers?
1 radian of a circle with a radius r is equal to the central angle at the center whose arc is equal to r. The radians are at the same distance on the number line.
We know that the length of an arc of a circle is \[\theta r\], where \[\theta \] is in radians.
Again, the length of an arc of a circle is \[\theta \times r \times \dfrac{{180}}{\pi }\] where \[\theta \] is in degree.
Interesting fact
Radian is the S I unit used for measuring angles.
The circumcircle of a circle is \[2\pi \] radian.
Solved examples
1. Visualize 3 radians on a circle.
Solution:
We know that one radian is equal to the central angle which makes an arc that length is equal to the radius of the circle.
Step 1: First we will draw a circle and measure the radius of the circle using a thread.
Step 2: Place the thread three times around the circle.
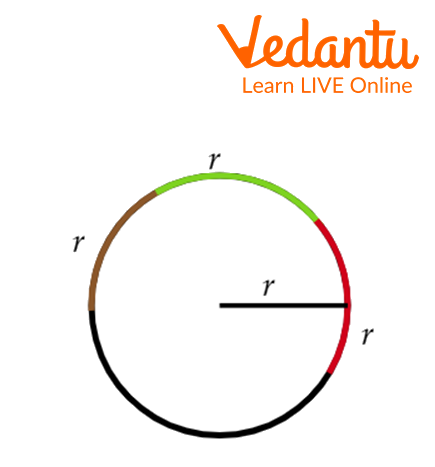
3 radians measuring
2. Convert \[3\pi \] in real number.
Solution: We know that 1 radian =57.296.
Thus multiply 57.296 with \[3\pi \] to get it in real number.
\[3\pi \times 57.296 = 171.88\pi \]
Putting the value of \[\pi \]
\[3\pi \times 57.296 = 171.88 \times \dfrac{{22}}{7}\]
\[3\pi \times 57.296 = 540.219\] (approx.)
3. Convert \[75^{\circ}\] into radian.
Solution: Multiplying \[\dfrac{\pi}{180^{\circ}}\] with \[75^{\circ}\] to convert into radian:
\[75^{\circ}=75^{\circ}\dfrac{\pi}{180^{\circ}}\]
\[\Rightarrow 75^{\circ}=\dfrac{5\pi}{12^{\circ}}\]
Therefore \[75^{\circ}=\dfrac{5\pi}{12^{\circ}}\]
Conclusion
Radian is the SI unit for measuring angles. Another unit for measuring angles is degrees. 1 radian = \[\dfrac{180^{\circ}}{\pi}\] and \[1^{\circ}=\dfrac{\pi}{180^{\circ}}\] radians. Radian measurements and real number measurements are the same.
The real value of one radian is 57.296(approx). The real value of radian is an irritation number.
Practices problem:
1. Convert \[4\pi \] radian into a real number.
Answer: 12.571(approx.)
2. Draw 1.5 radians on a circle.
Answer:
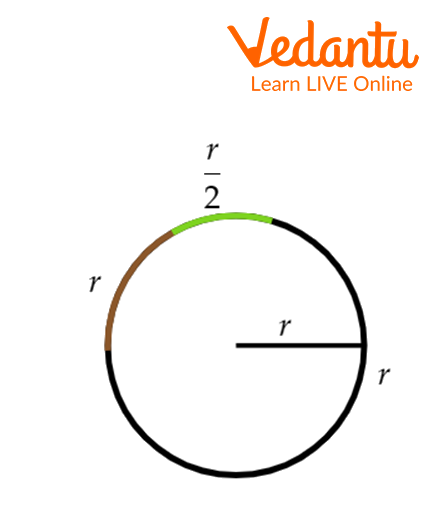
1.5 radians
List of related articles
FAQs on Understand the Relation Between Radian and Real Numbers
1. What is the fundamental relationship between radian and real numbers as per the Class 11 Maths syllabus?
The fundamental relationship is that any real number can represent a radian measure, and vice-versa. We can visualise this by wrapping a real number line around a unit circle (a circle with radius 1). The point on the number line that corresponds to a point on the circle's circumference creates an angle. The measure of this angle in radians is equal to the real number representing the arc's length from the starting point (1, 0).
2. How does a unit circle visually explain the one-to-one correspondence between real numbers and radians?
A unit circle (where the radius is 1 unit) is a perfect tool for this. Here's how it works:
- Imagine a real number line placed vertically, with its zero at the point (1, 0) on the circle.
- When you wrap this line around the circle, every unique real number maps to a unique point on the circumference.
- The arc length from the starting point (1, 0) to this new point is equal to the real number.
- The central angle subtended by this arc is defined to have a measure equal to that real number in radians. This creates a direct, visual link between any real number and an angle measure.
3. Why are radians often preferred over degrees in higher mathematics like calculus?
Radians are preferred because they are a more 'natural' and dimensionless unit for measuring angles. They are derived directly from a circle's properties (the ratio of arc length to radius), unlike degrees, which are based on an arbitrary division of a circle into 360 parts. This natural relationship simplifies many important formulas in calculus and physics, such as the derivatives of trigonometric functions (e.g., the derivative of sin(x) is cos(x) only when x is in radians).
4. What is the formula that connects arc length, radius, and the angle in radians?
The formula is l = rθ, where:
- l is the length of the arc.
- r is the radius of the circle.
- θ (theta) is the angle subtended by the arc at the centre, measured in radians.
5. What is the basic rule to convert an angle from degrees to radians and vice versa?
The conversion is based on the relationship that a full circle is 360°, which is equal to 2π radians. This simplifies to 180° = π radians. From this, we get two rules:
- To convert degrees to radians, multiply the angle by (π / 180°).
- To convert radians to degrees, multiply the angle by (180° / π).
6. Can a radian measure be an integer or a fraction, or must it always involve π?
This is a common point of confusion. A radian measure can be any real number. While π is frequently used because it relates to a half or full circle, an angle can be 1 radian, 2.5 radians, or 4/3 radians. An angle of 1 radian is simply the angle where the arc length equals the radius. It does not have to be an expression involving π.
7. What is the formal definition of 1 radian?
One radian is defined as the measure of a central angle that subtends an arc whose length is exactly equal to the radius of the circle. So, if a circle has a radius 'r', the angle that carves out an arc of length 'r' on the circumference is 1 radian. Numerically, 1 radian is approximately 57.3°.
8. How are both positive and negative real numbers accounted for in the radian system?
The sign of the real number corresponds to the direction of rotation for the angle. As per convention:
- A positive real number (e.g., +2 radians) corresponds to an angle measured in the counter-clockwise direction from the positive x-axis.
- A negative real number (e.g., -2 radians) corresponds to an angle measured in the clockwise direction from the positive x-axis.















