




How to Calculate the Perimeter of Different Figures
The route or boundary that encircles any shape in mathematics is defined by the shape's circumference. To put it another way, the circumference and perimeter both refer to the length of a shape's outline.
What is the Perimeter?
A path that encircles a two-dimensional object is called a perimeter. The word is Greek, peri meaning "around," and "metre" meaning measure. The phrase can refer to either the path or its length; it can be compared to the size of a shape's outline.
How to Find the Perimeter of a Figure?
Steps to find the Perimeter of a given figure:
STEP 1 : Calculate the lengths of the sides.
Usually we don't need a special formula to get perimeter because perimeter is simply a measure of a two-dimensional figure's outline (though there are equations for specific shapes to make it easier).
STEP 2 : The length of each side is added together.
When calculating the perimeter of a non-circular object, add up all of the side lengths to get its perimeter.
STEP 3 : Be careful of the units of measurement.
We need to add all the lengths in the same unit to add else we can't add it (such as feet, miles, or metres).
Perimeter of Square:
Since a square is a polygon with four equal sides, its perimeter will be equal to the sum of those sides.
The formula \[{\rm{P = 4x}}\], where x is the length of one side, can be used to determine whether a square has four equal-length sides.

Square
Perimeter of Rectangle:
The perimeter of a rectangle is determined by adding up all of its sides.
Formula \[ = 2(a + b)\] units
where:
“a” is the length of the rectangle
“b” is the breadth of the rectangle

Rectangle
Perimeter of Circle:
Circumference of the circle or perimeter of the circle is the measurement of the boundary of the circle.
Circle perimeter or circumference is equal to\[2\pi r\] .
where,
r is the circle's radius.
\[\Pi \] is a mathematical constant with an estimated value of 3.14 (to the nearest two decimal places).

Circle
Solved Examples:
1: Find the perimeter of the square whose side is 6 units.
Ans: As we know that all the sides of a square are equal.
And its perimeter is 4 times its side.
Thus, it’s perimeter will be \[4 \times 6 = 24\]
Its perimeter is 24 units.
2: Find the perimeter of the following figure:
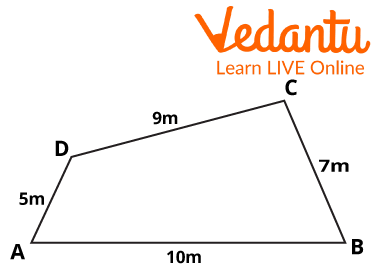
Ans: The perimeter of a planar object is the sum of all the sides in it.
It can alternatively be described as the total sum of all of a planar object's bounding sides.
Here,\[AB + BC + CD + DA = 5 + 9 + 7 + 10\] is the total length of all the sides of the provided figure.
Thus, The stated figure's perimeter is 31 metres.
3 :Determine the circle's radius for\[C = 50cm\] .
Ans: Given that 50 cm is the circumference.
According to the formula\[C = 2\pi r\]
This indicates that
\[\begin{array}{l}50 = 2\pi r\\25 = \pi r\\r = 25/\pi \end{array}\]
As a result, the circle's radius is \[25/\pi \] cm.
Conclusion:
Any 2D shape's perimeter can be calculated by labelling and adding the sides. When calculating the perimeter, don't forget to account for the length of each side. For instance, the lengths of a rectangle's two widthwise edges and its two lengthwise borders are added to form the rectangle's perimeter and similar for other shapes also.
FAQs on Perimeter of a Figure: Definition, Formula & Examples
1. What is the perimeter of a figure?
The perimeter is the total distance around the boundary of a closed, two-dimensional figure. Think of it as walking along the edges of a park; the total distance you cover is its perimeter. It is calculated by adding the lengths of all its sides. For example, if a triangle has sides of 3 cm, 4 cm, and 5 cm, its perimeter would be 3 + 4 + 5 = 12 cm.
2. What are the formulas for finding the perimeter of common shapes like squares and rectangles?
While the basic method is to add all side lengths, simple formulas exist for regular shapes to make calculations faster. The most common formulas are:
Square: Since all four sides are equal, the formula is Perimeter = 4 × side.
Rectangle: As opposite sides are equal, the formula is Perimeter = 2 × (length + breadth).
Triangle: The perimeter is the sum of its three sides: Perimeter = side a + side b + side c.
3. How do you calculate the perimeter of an irregular figure?
To find the perimeter of an irregular figure, which is a shape with sides of different lengths, you must measure and then add the length of each individual side. There isn't a shortcut formula. You simply sum up all the boundary lengths. If a side's length is unknown, you might need to use other given information about the figure to find it first.
4. What is the circumference of a circle and how is it related to perimeter?
The circumference is the special term used for the perimeter of a circle. It represents the total length of the curved boundary of the circle. It is calculated using the formula Circumference = 2 × π × r, where 'r' is the circle's radius and π (pi) is a mathematical constant (approx. 3.14). Essentially, circumference is just the perimeter concept applied to a round shape.
5. What is the key difference between the perimeter and the area of a shape?
The main difference is what each one measures:
Perimeter measures the length of the outer boundary of a shape. It's a one-dimensional measurement (units: cm, m, km).
Area measures the space enclosed within that boundary. It's a two-dimensional measurement (units: cm², m², km²).
For example, the fence around a garden represents its perimeter, while the lawn inside the fence represents its area.
6. When calculating perimeter, should I add or multiply the side lengths?
You must always add the lengths of all the sides to determine the perimeter. Multiplication is only a shortcut used for regular polygons where all sides are equal (like a square or equilateral triangle). For instance, for a square with a side of 5 cm, you can multiply 4 × 5 instead of adding 5+5+5+5. Confusing this with multiplying length by breadth gives you the area, which is incorrect for perimeter.
7. Can you give some real-life examples where the concept of perimeter is used?
Yes, we use the concept of perimeter frequently in our daily lives. Some common examples include:
Fencing a garden or yard to calculate the total length of fencing material required.
Framing a photograph to determine the amount of wood or metal needed for the frame.
Laying a running track to measure the exact distance of one lap.
Putting a decorative border on a wall, a table, or a piece of cloth.
8. Can two different shapes have the same perimeter?
Yes, absolutely. Two or more figures with completely different shapes can have the exact same perimeter. For example, take a piece of string that is 24 cm long. You can arrange it to form:
A square with each side being 6 cm (Perimeter = 4 × 6 = 24 cm).
A rectangle with a length of 8 cm and a breadth of 4 cm (Perimeter = 2 × (8 + 4) = 24 cm).
An equilateral triangle with each side being 8 cm (Perimeter = 8 + 8 + 8 = 24 cm).
Even though their shapes and areas are different, their perimeters are identical.















