Parallelogram on the Same Base and Between the Same Parallels

The term ‘parallelogram’ was derived from the Greek word ‘parallelogrammon’, which stands for “bounded by parallel lines.” Hence, a parallelogram is a quadrilateral that is bounded by parallel lines. It is a shape in which the opposite sides are parallel and equal.

Parallelograms are classified into three main types: square, rectangle, and rhombus, and each of them has its unique properties. In this section, we will learn about a parallelogram, its theorem, and other aspects related to a parallelogram, along with the solved examples.

Showing Geometrical Shapes or Figures

What Is a Parallelogram?

A parallelogram is a special kind of quadrilateral formed by parallel lines. A quadrilateral will be a parallelogram if its opposite sides are parallel and congruent. The angle between the adjacent sides of a parallelogram may vary, but the opposite sides must be parallel. Hence, a parallelogram is defined as a quadrilateral in which both pairs of opposite sides are parallel and equal.

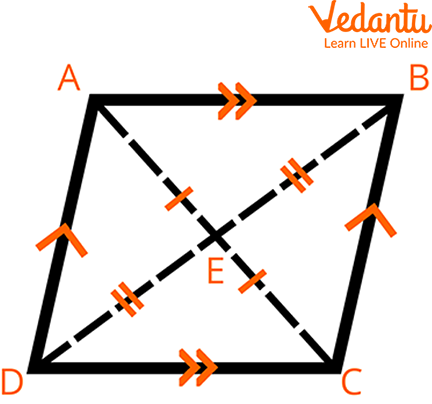
Parallelogram ABCD

Properties of a Parallelogram

1. The number of vertices and edges in a parallelogram are 4 and 4, respectively.

2. It is a convex polygon having 0 lines of symmetry.

3. The perimeter of a parallelogram is given by twice the sum of the length of adjacent sides.

4. The product of the base and corresponding height gives the area of a parallelogram.

5. Diagonals of a parallelogram bisect each other and divide it into four triangles of equal area.

Theorem: To Prove That Parallelograms on the Same Base and Between the Same Parallels Are Equal in Area

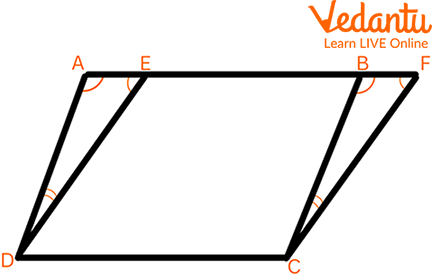
Two Parallelograms ABCD and EFCD with a Common Base DC

Given: Two parallelogram ABCD and EFCD on the same base DC and between the same parallels AF and DC

To prove: $\operatorname{ar}(A B C D)=\operatorname{ar}(E F C D)$

Proof: In triangle $A D E$ and $B C F$,

$\angle D A E=\angle C B F \ldots(1)$ Corresponding angles

(AD||BC and $A F$ is a transversal that intersects them)

$\angle \mathrm{AED}=\angle \mathrm{BFC} \ldots(2)$Corresponding angles

ED $|| {FC}$ and $\mathrm{AF}$ is a transversal that intersects them)

Also, $A D=B C$...(3).....Opposite sides of the parallelogram $A B C D$

Using equations 1,2 and 3, we get

Triangle ADE and triangle BCF are congruent to each other by the ASA congruence rule

Thus, area of triangle $\mathrm{ADE}=$ area of triangle $\mathrm{BCF}$

Adding area EDCB on both sides, we get

$\operatorname{ar}($ triangle $\mathrm{ADE})+\operatorname{ar}(\mathrm{EDCB})=\operatorname{ar}($ triangle $\mathrm{BCF})+\operatorname{ar}(\mathrm{EDCB})$

$\operatorname{ar}(|| A B C D)=\operatorname{ar}(|| E F C D)$

So, parallelograms $A B C D$ and $E F C D$ with common base $D C$ are equal in area.

Hence Proved.

Solved Examples

Question: Parallelograms PQRS and PQTU are on the same base PQ and between parallel lines PQ and UR. Find the length of the common side of two parallelograms. The area of the parallelogram PQRS = 144 $cm^2$, and the altitude of the parallelogram PQTU = 16 cm.

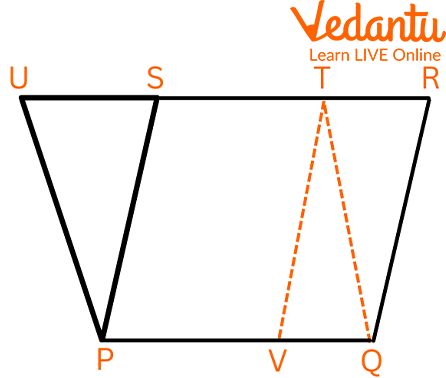
Two Parallelograms on the Same Base

Ans: The length of the common side of two parallelograms is 9 cm.

Given: Two parallelograms, PQRS and PQTU, are on the same base and between the same parallels.

$\operatorname{ar}(|| P Q R S)=144 \mathrm{~cm}^2$

Altitude of I|gm PQTU is $16 \mathrm{~cm}$

To find: Length of the common side, i.e. PQ

Proof: Using theorem and given, we get

$\operatorname{ar}(|| \mathrm{PQRS})=\operatorname{ar}(|| \mathrm{PQTU})=144 \mathrm{~cm}^2$

base $\times$ altitude $=144$

base $\times 16=144$

base $=9 \mathrm{~cm}$

Thus, the length of the same base is $9 \mathrm{~cm}$.

Practice Problems

Some problems based on the parallelogram having the same base and between the same parallels are given under:

Q 1. Parallelograms PQRS and PQTU are on the same base PQ and between the same parallels PQ and UR. The area of parallelogram PQRS = 56 cm2 and the altitude of the parallelogram PQTU = 7 cm. Find the length of the common side of two parallelograms.

Ans: 8 cm

Q 2. In which of the following figures, did you find two polygons on the same base and between the same parallels?

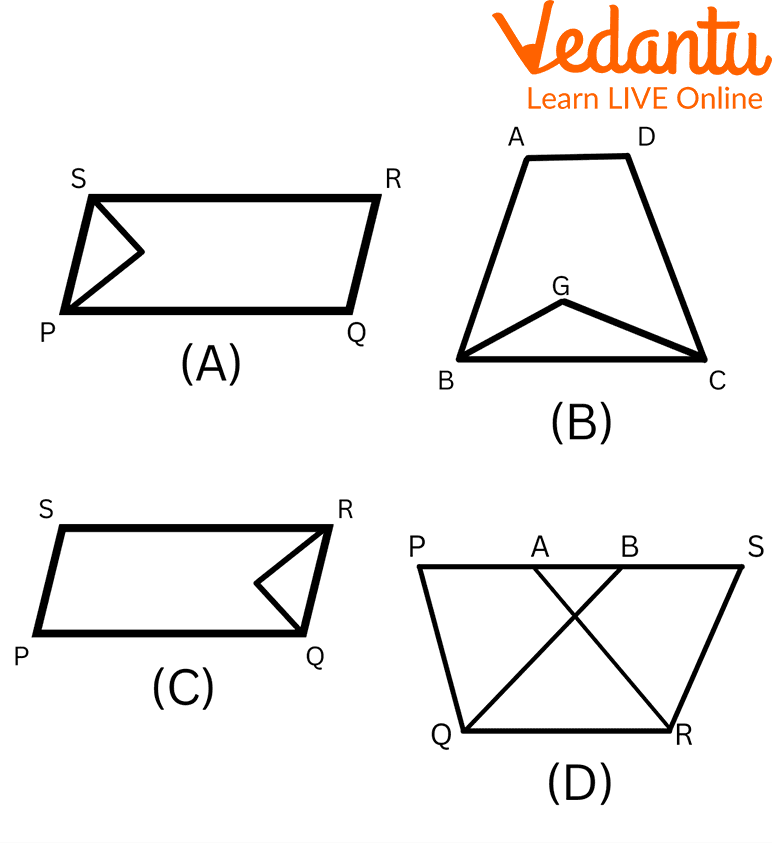
Polygons

Ans: Figure D

Summary

Let’s sum up with the concept of a parallelogram and its properties. Here we discussed in depth the theorem to prove that the parallelogram on the common base and between the same parallels are equal in area. The main motive of this article was to teach the students about the easiest way of proving the theorem. Some practice problems have been shared for the students, so they gain deep proficiency in the concept. We hope the article helped you understand the properties and theorems based on parallelograms and that you enjoyed reading it.