




Introduction
The magnitude (modulum) of the product of two adjacent vectors, which are thought of as vectors, determines the area of a parallelogram. A parallelogram's opposing sides are of equal length (congruent). In a parallelogram, the opposing angles are equal in size. Two adjacent vertices' angles can be any multiple of 180 degrees. Each parallelogram's inside angles add up to 360° in total.
In today's lesson, we will show that the opposite sides of a parallelogram are equal.
A parallelogram is a quadrilateral where the two opposite sides are parallel. We will show that, in that case, they are also equal.
What is Parallelogram
A parallelogram is a geometric object with sides that are parallel to one another in two dimensions. It is a form of polygon with four sides (sometimes known as a quadrilateral) in which each parallel pair of sides have the same length. A parallelogram has neighbouring angles that add up to 180 degrees. You must have studied a variety of 2D forms and sizes in geometry, including circles, squares, rectangles, rhombuses, etc. Each of these forms has a unique set of characteristics.
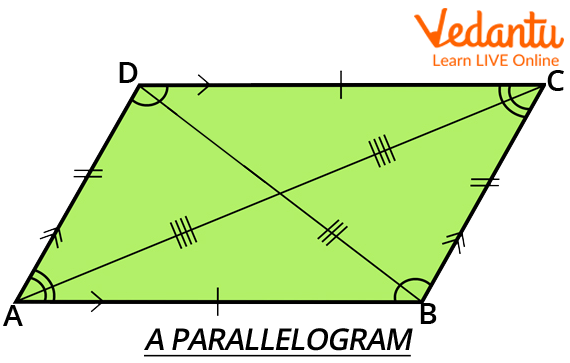
A Parallelogram
Definition
A quadrilateral having two sets of parallel sides is referred to as a parallelogram. In a parallelogram, the opposing sides are of equal length, and the opposing angles are of equal size. Additionally, the interior angles that are additional to the transversal on the same side. 360 degrees is the sum of all interior angles.
A parallelepiped is a three-dimensional shape with parallelogram-shaped faces. The base (one of the parallel sides) and height (the distance from top to bottom) of the parallelogram determine its area. A parallelogram's perimeter is determined by the lengths of its four sides.
The qualities of a parallelogram are shared by the forms of a square and a rectangle.
Theorem of Parallelogram
The forms that result from moving from one point to the next while holding a pencil with a sharp tip on a piece of paper are known as plane curves. A simple curve is one that does not cross itself at any point. A polygon is a straightforward closed planar curve consisting entirely of line segments.
A parallelogram is a polygon. A parallel quadrilateral with both sets of opposing sides is known as a parallelogram. We shall gain in-depth information on the theorems and characteristics of parallelograms in this post.
Theorem : In a parallelogram, opposite sides are equal.
Given:
Solution: Let ABCD be a parallelogram and AC be a diagonal.
Observe that the diagonal AC divides parallelogram ABCD into two triangles: \[\Delta ABC\] and\[\Delta CDA\].
We need to first prove that these triangles are congruent.
In \[\Delta ABC\] and \[\Delta CDA\]; note that \[BC{\rm{ }}||{\rm{ }}AD\] and AC is a transversal.
So, \[BCA{\rm{ }} = {\rm{ }}DAC\] (Pair of alternate angles)
And \[AC{\rm{ }} = {\rm{ }}CA\] (common)
So, \[\Delta ABC\] and \[\Delta CDA\]; are congruent (ASA rule).
Therefore, the corresponding parts \[AB{\rm{ }} = {\rm{ }}CD\] and \[AD{\rm{ }} = {\rm{ }}BC\]
Hence proved.
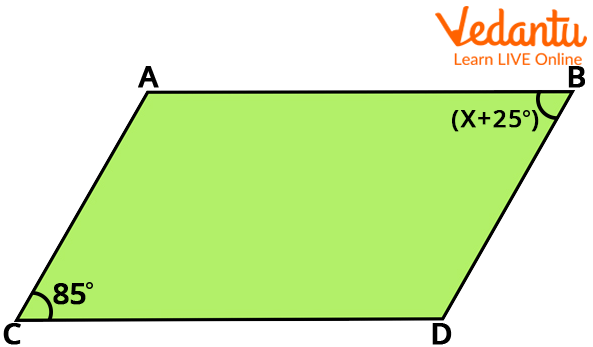
Parallelogram Theorem
Solved Questions
1. Find the area of parallelogram ABCD if AE : EB = 1 : 2.
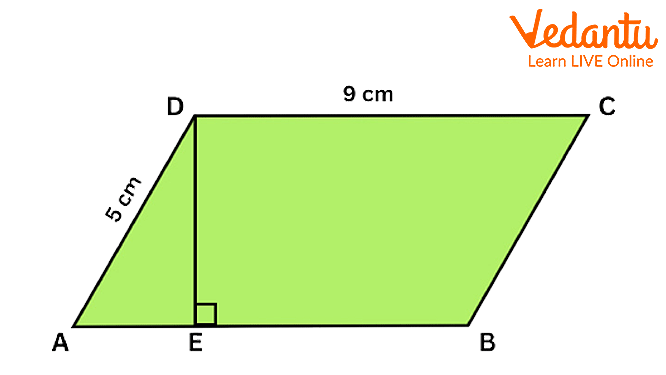
Question 1
a) 25 sqm
b) 22.5 sqm
c) 36 sqm
d) 45 sqm
Answer: c
Explanation: In parallelogram ABCD, AB = CD = 9cm (Opposite sides of a parallelogram are equal)
Now, \[AE{\rm{ }}:{\rm{ }}EB{\rm{ }} = {\rm{ }}1{\rm{ }}:{\rm{ }}2\]and \[AE{\rm{ }} + {\rm{ }}EB{\rm{ }} = {\rm{ }}AB\]
\[ \Rightarrow k{\rm{ }} + {\rm{ }}2k{\rm{ }} = {\rm{ }}9 \Rightarrow k{\rm{ }} = {\rm{ }}3\]
\[ \Rightarrow AE{\rm{ }} = {\rm{ }}3cm\]
In \[\Delta AED,{\rm{ }}A{D^2}\; = {\rm{ }}A{E^2}\; + {\rm{ }}E{D^2}\] (By Pythagoras theorem)
\[ \Rightarrow {5^2}\; = {\rm{ }}{3^2}\; + {\rm{ }}E{D^2}\]
\[ \Rightarrow E{D^2}\; = {\rm{ }}25{\rm{ }}--{\rm{ }}9{\rm{ }} = {\rm{ }}16\]
\[ \Rightarrow ED{\rm{ }} = {\rm{ }}4cm\]
Now, Area of parallelogram ABCD = Base x corresponding altitude \[ = {\rm{ }}AB{\rm{ }} \times {\rm{ }}DE{\rm{ }} = {\rm{ }}9{\rm{ }} \times 4{\rm{ }} = {\rm{ }}36sqm.\]
2. In the parallelogram ABCD, \[\angle ABC{\rm{ }} = {\rm{ }}50^\circ \]. Find the measures of \[\angle BCD,\angle CBA\] and \[\angle DAB.\]
Solution:
As\[AB\parallel DC,\angle ABC{\rm{ }} + \angle BCD{\rm{ }} = {\rm{ }}180^\circ \]
Therefore, \[\angle BCD{\rm{ }} = {\rm{ }}180^\circ - \;\angle ABC\]
\[ = {\rm{ }}180^\circ {\rm{ }} - \;50^\circ \]
\[ = \;130^\circ \]
As opposite angles in a parallelogram are equal,
\[\angle CDA{\rm{ }} = \angle ABC{\rm{ }} = {\rm{ }}50^\circ \] and
\[\angle DAB{\rm{ }} = \angle BCD{\rm{ }} = {\rm{ }}130^\circ \]
3. Find the value of x if PQRS is a parallelogram.
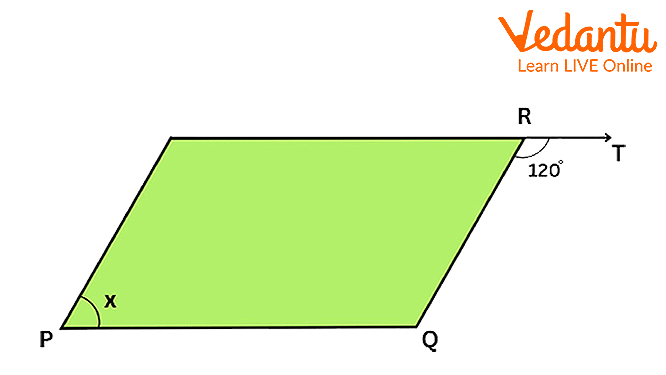
Question 3
a) \[150^\circ \]
b) \[50^\circ \]
c) \[60^\circ \]
d) \[120^\circ \]
Answer: c
Explanation: \[\angle SRQ{\rm{ }} + \angle QRT{\rm{ }} = {\rm{ }}180^\circ \] (Linear Pair)
\[ \Rightarrow \angle SRQ{\rm{ }} = {\rm{ }}60^\circ \]
In parallelogram PQRS, \[\angle SRQ{\rm{ }} = \angle QPS\] (Opposite angles of a parallelogram are equal)
\[ \Rightarrow x{\rm{ }} = {\rm{ }}60^\circ .\]
Conclusion
This article covered our study of the parallelogram. A parallelogram is a quadrilateral with two pairs of parallel sides. A parallelogram has opposite sides of the same length and angles of the same size. the internal angles on the same side that are in addition to the transversal. The total of all internal angles is 360 degrees. And the theorem that establishes the equality of the opposing sides of a parallelogram.
FAQs on Opposite Sides are Equal
1. What is the fundamental property of a parallelogram concerning its sides?
A parallelogram is a quadrilateral with two pairs of parallel sides. The fundamental property that arises from this definition is that its opposite sides are always equal in length. For a parallelogram labelled ABCD, the length of side AB will be equal to the length of the opposite side DC, and the length of side AD will be equal to the length of the opposite side BC.
2. How can you prove that the opposite sides of a parallelogram are equal?
The proof that a parallelogram's opposite sides are equal is a core concept in Class 9 geometry. It is done by using congruent triangles, as per the NCERT syllabus:
- Start with a parallelogram ABCD and draw a diagonal, for instance, AC.
- This diagonal splits the parallelogram into two triangles: ΔABC and ΔCDA.
- Since opposite sides are parallel (BC || AD and AB || DC), the alternate interior angles are equal (∠BCA = ∠DAC and ∠BAC = ∠DCA).
- The diagonal AC is a common side to both triangles.
- By the Angle-Side-Angle (ASA) congruence rule, ΔABC is congruent to ΔCDA.
- Therefore, their corresponding parts must be equal, which means AB = CD and BC = DA.
3. What are the primary properties that define a parallelogram?
A parallelogram is defined by several key properties that are crucial for solving geometry problems:
- Opposite sides are parallel (this is the definition).
- Opposite sides are equal in length.
- Opposite angles are equal in measure.
- Consecutive angles are supplementary, meaning they add up to 180°.
- The diagonals bisect each other, meaning they intersect at their midpoints.
4. Can you provide some real-world examples of parallelograms?
Yes, the parallelogram shape appears in many everyday objects and structures. Some common examples include:
- The surfaces of many desks and tables.
- The individual glass panes in some modern building facades.
- The shape of a standard pencil eraser.
- The layout of some solar panel arrays to maximise sun exposure.
- Stripes or patterns on fabric and clothing.
5. If a quadrilateral has opposite sides of equal length, is it guaranteed to be a parallelogram?
Yes, this is the converse of the theorem. If a quadrilateral has two pairs of opposite sides that are equal in length, it is guaranteed to be a parallelogram. This property is very useful because it provides another way to test and prove if a given four-sided shape is a parallelogram without having to check if the sides are parallel.
6. How does the 'opposite sides are equal' property relate to shapes like rectangles and squares?
Rectangles, squares, and rhombuses are all special types of parallelograms. This means they inherit all the properties of a parallelogram, including having opposite sides of equal length. The distinctions are:
- A rectangle is a parallelogram where all angles are 90°.
- A rhombus is a parallelogram where all four sides are equal.
- A square is both a rectangle and a rhombus; it is a parallelogram with all 90° angles and all four sides equal.
7. Are the diagonals of a parallelogram also equal, similar to its opposite sides?
No, this is a common misconception. In a general parallelogram, the diagonals are not equal in length. While they always bisect each other (cut each other in half), their total lengths are different. The only parallelograms that have equal diagonals are its special forms: the rectangle and the square.
8. Why is it important to understand that a parallelogram's opposite sides are equal?
This property is a foundational concept in geometry for several reasons. It is essential for:
- Calculating the perimeter of a parallelogram, as you only need the lengths of two adjacent sides.
- Forming the basis for area formulas.
- Solving for unknown lengths in geometric figures and coordinate geometry problems.
- Proving other key theorems about quadrilaterals and their properties.





















