




Key Rules and Examples for Multiplying Mixed Numbers
What Are Mixed Numbers?
Mixed numbers, also known as mixed fractions, are a combination of whole numbers and a proper fraction. The mixed number is partly a whole number and partly a fraction. The fractional part of a mixed number is always a proper fraction. For example, 534, 712, 723, etc are mixed numbers. Multiplying mixed numbers is similar to multiplying fractions. Here, we will learn the steps to multiply mixed numbers with the like denominators, unlike denominators, and whole numbers.
Parts of Mixed Number
A mixed number is formed by combining three parts namely the whole number, a numerator, and a denominator. Look at the image given to understand the parts of mixed numbers in a better way.
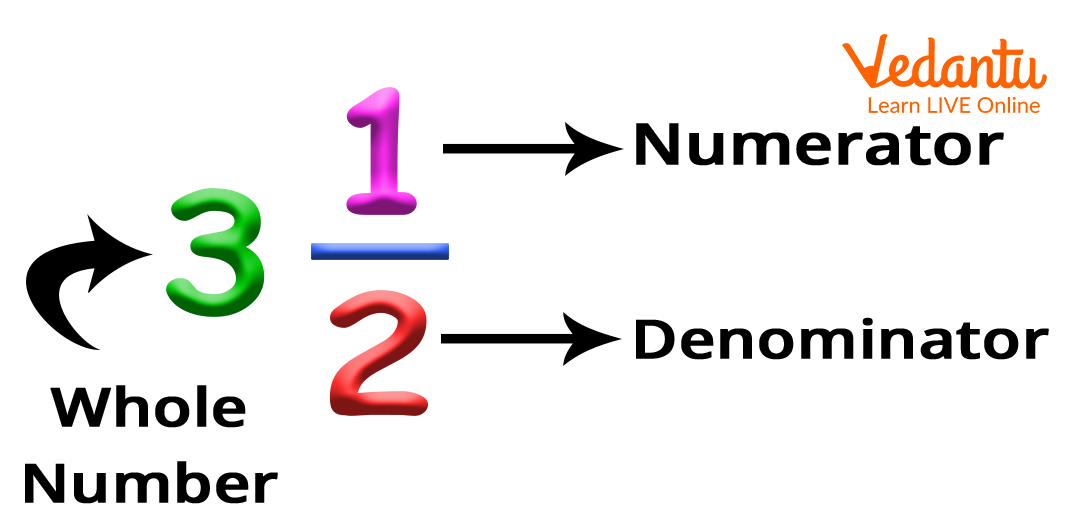
How to Multiply Two Mixed Numbers with Like and Unlike Denominators?
Two fractions with the same denominator are known as the like denominators. Contrarily, two fractions with different denominators are known as unlike denominators. The steps to multiply the mixed fractions remains the same irrespective of the like or unlike denominators. The 4 steps given below describes how to multiply mixed numbers with like and unlike denominators:
Step 1: Convert the given mixed numbers into improper fractions.
Step 2: Multiply first the numerators and and then the denominators of the improper fraction.
Step 3: Simplify the fraction or result obtained in the previous step in lowest terms if possible.
Step 4: Convert the result obtained back to the mixed number.
How to Convert a Mixed Number into an Improper Fraction?
To convert a mixed number into an improper fraction:
Multiply the whole number with the denominator of the proper fraction.
Add the numerator of the proper fraction to the product obtained in step 1.
The denominator of the improper fraction will be the same as the denominator of the proper fraction.
The resulting fraction will be an improper fraction.
Let us understand with an example:
Convert 512 into an improper fraction.
Solution:
Step 1: Multiplying the whole number with the denominator of the proper fraction.
5 2 = 10
Step 2: Adding the numerator of the proper fraction to the product obtained in step 1. Here, the numerator is 1. Accordingly, numerator of the improper fraction will be 10 + 1 = 11
Step 3: The denominator of the improper fraction will stay the same. Accordingly, the denominator will be 2.
Hence, 512 in improper fraction will be 112.
As we have understood how to convert mixed number to an improper fraction, let us now understand multiplying mixed number with an example:
Example on Multiplying Mixed Numbers with Like Denominators
What is 2 27 3 17 ?
Solution:
Step 1: Converting the mixed numbers into improper fractions, we have
2 27 = 2 7 + 27 = 167
3 17 = 3 7 + 17 = 227
Step 2: Multiplying the numerators and denominators of improper fractions obtained in step 1.
167 227 = 35249
Step 3: Converting the final result back into the mixed fraction. Accordingly, 35249 = 7949
Therefore, 2 27 3 17 = 7949
Example on Multiplying Mixed Numbers with Unlike Denominators
What is 1 23 2 34 ?
Solution:
Step 1: Converting the mixed numbers into improper fractions, we have
1 23 = 3 1 + 23 = 53
2 34 = 2 4 + 34 = 114
Step 2: Multiplying the numerators and denominators of improper fractions obtained in step 1.
53 114 = 5512
Step 3: Converting the final result back into the mixed fraction. Accordingly, 5512 = 4712
Therefore, 1 23 2 33 = 4712
How to Multiply Mixed Numbers with the Whole Number?
The steps on multiplying the mixed number with the whole number are discussed below:
Step 1: Convert the whole number into fraction assuming the denominator to be 1.
Step 2: Convert the given mixed numbers into improper fractions.
Step 3: Multiply the numerators and denominators of the fraction.
Step 4: Simplify the result or fraction obtained in the previous step in lowest terms if possible.
Step 5: Convert the result obtained back to the mixed number.
Let us understand with an example:
What is 216 3?
Solution:
Step 1: Converting the whole number into fraction assuming the denominator to be 1. Hence, 3 will be 31
Step 2: Converting the given mixed number into improper fraction gives: 216 = 136
Step 3: Multiplying the numerators and denominators of the fraction gives:
136 31 = 396
Step 4: Simplifying the fraction obtained in the previous step in lowest terms gives:
396 = 39 36 3 = 132
Step 5: Converting the result obtained back to the mixed number gives:
132 = 6 12
Therefore, 216 3 = 6 12
In short, multiplying mixed numbers with fractions is a four-step process. Here, first you have to convert a given mixed number into an improper fraction, multiply the numerator and denominator of the fraction. Simplify the result if possible and convert the result back to the mixed number.
FAQs on Multiplying Mixed Numbers Made Easy
1. What is the step-by-step method to multiply mixed numbers?
Multiplying mixed numbers involves a simple, three-step process to ensure accuracy. Following these steps makes the calculation straightforward:
Step 1: Convert to Improper Fractions: Change each mixed number into an improper fraction. To do this, multiply the whole number by the denominator and add the numerator. This result becomes the new numerator, while the denominator stays the same.
Step 2: Multiply the Fractions: Multiply the numerators of the improper fractions together to get the new numerator. Then, multiply the denominators together to get the new denominator.
Step 3: Simplify and Convert Back: If the resulting fraction is improper, convert it back into a mixed number by dividing the numerator by the denominator. The quotient is the whole number, the remainder is the new numerator, and the denominator remains the same. Always simplify the fraction to its lowest terms if possible.
2. Why must mixed numbers be converted into improper fractions before multiplying?
You must convert mixed numbers into improper fractions because it's the only way to multiply the entire value of each number correctly. A mixed number is a sum of a whole number and a fraction (e.g., 2 ½ is 2 + ½). If you only multiplied the whole parts and the fraction parts separately, you would miss the cross-multiplication component and get an incorrect answer. Converting to an improper fraction (like 5/2) combines the whole and fractional parts into a single fractional form, allowing for a direct and accurate multiplication of the total values.
3. Can you provide a clear example of multiplying two mixed numbers?
Certainly. Let's multiply 3 ½ by 2 ¼.
First, convert both mixed numbers to improper fractions. For 3 ½, we calculate (3 × 2) + 1 = 7, so it becomes 7/2. For 2 ¼, we calculate (2 × 4) + 1 = 9, so it becomes 9/4.
Next, multiply the numerators: 7 × 9 = 63.
Then, multiply the denominators: 2 × 4 = 8.
The result is 63/8. To convert this back to a mixed number, we divide 63 by 8. It goes in 7 times (56) with a remainder of 7. So, the final answer is 7 ⅞.
4. What is the process for multiplying a mixed number by a whole number?
To multiply a mixed number by a whole number, you follow a similar process. First, convert the mixed number into an improper fraction. Then, write the whole number as a fraction by placing it over 1. For example, to multiply 4 ⅓ by 5:
Convert 4 ⅓ to an improper fraction: (4 × 3) + 1 = 13, so you get 13/3.
Write the whole number 5 as a fraction: 5/1.
Multiply the fractions: (13 × 5) / (3 × 1) = 65/3.
Convert the result back to a mixed number: 65 divided by 3 is 21 with a remainder of 2. The final answer is 21 ⅔.
5. What is a common mistake to avoid when multiplying mixed numbers?
The most common mistake is multiplying the whole numbers and the fractions separately and then adding them. For instance, when multiplying 2 ½ by 3 ⅓, students might incorrectly calculate (2 × 3) + (½ × ⅓) = 6 + ⅙ = 6 ⅙. This is wrong because it ignores the distributed values. The correct method is to convert to improper fractions (5/2 × 10/3), multiply to get 50/6, and then simplify to 25/3, which is 8 ⅓. Always remember to convert to improper fractions first to avoid this critical error.
6. How is multiplying mixed numbers different from adding them?
The key difference lies in the initial step. For multiplication, you must convert the mixed numbers into improper fractions. For addition, you have two options: you can either convert to improper fractions (often necessary if regrouping is needed) or you can add the whole numbers and the fractions separately and then combine them. The mandatory conversion for multiplication ensures that the entire quantities are multiplied, whereas addition allows for separating the whole and fractional parts.
7. Why is it important to simplify the final answer when multiplying fractions?
Simplifying the final answer to its lowest terms is a crucial step for clarity and standardisation. An answer like 8/16 is correct, but it is not as easy to understand as its simplified form, ½. Simplification presents the fraction in its most concise and recognisable form, which is essential for comparing results, understanding proportions, and for use in subsequent calculations. As per the CBSE/NCERT curriculum, answers in fractions are expected to be presented in their simplest form.
8. Where might we use the multiplication of mixed numbers in a real-life scenario?
Multiplying mixed numbers is very common in everyday tasks. A great example is in cooking or baking when you need to adjust a recipe. If a recipe calls for 1 ¾ cups of flour and you want to make 2 ½ times the quantity, you would multiply 1 ¾ by 2 ½ to find the new amount of flour needed. It's also used in construction for measuring materials, like calculating the area of a room that has fractional dimensions, for example, 10 ½ feet by 12 ¼ feet.





















