




How to Solve Multi Digit Multiplication Problems Easily
In our earlier classes, we learned about all four maths operations: addition, subtraction, multiplication and division. And from all the operations, our favourites were addition and multiplication because they were simpler than subtraction and division. But today in this article, we will learn about multi-digit multiplication in a very easy and enjoyable way. Doing multiplication is fun if it's done in the right way. So in this article, we will learn about 5 digit multiplication, which we might call hard multiplication. Here we provided multiplication practice problems and 3-digit multiplication worksheets to clear your concepts.
What is Multiplication?
Multiplication is an important arithmetic operation; it helps to find the total number of items quickly. It's the operation representing the basic idea of repeated addition of the same number. So we can say that it's a method of finding the product of two or more numbers. We use multiplication in our everyday life. Do you want to know how?
So let's say you went to a grocery store to buy 5 apples, which cost 10 rupees. How much money do you need to pay to buy those 5 apples? Do you know the answer? Ok, stop, don't waste your time adding them repeatedly; just multiply 5 by 10, so the answer is 50. So you will need 50 rupees to buy those 5 apples.
Here we understand multiplication and why we need it, we find it interesting, too, so don't worry. We are not going to stop here. We are going to explore multiplication a little bit more. We are going to learn about multi-digit multiplication.
Symbol of Multiplication
While doing multiplication, there are many symbols which are used to denote the most interesting arithmetic operation, i.e. multiplication. So let's check what symbols are used to denote multiplication.
Cross sign “X”, dot sign “.”, and the star sign “*”. And remember, if there is no symbol after the bracket, there is also multiplication between the numbers. Confused? Don't worry. Let's check it with an example 5(7)= 35.

Symbol of multiplication
Formula for Multiplication
The multiplication formula is very simple. Let's see what it is, Multiplicand x Multiplier = Product. Where multiplicand refers to the first number, the total number of objects in each group. Then Multiplier is the second number which is the number of equal groups.
And the last is the product which is the final result that we get after multiplying the multiplicand and the multiplier.
Example: If a multiplier is 6 and multiplicand is 5, the product is 30.
12 x 10 = 120
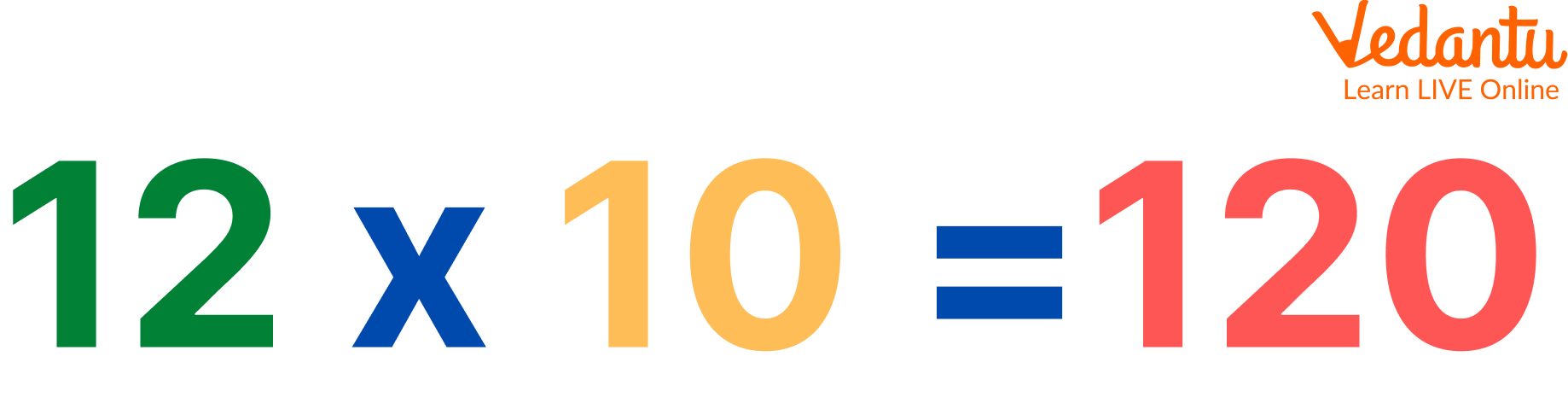
Multiplication
Rules for Multiplication
If any number is multiplied by 0, the product will be 0.
Example: $5 \times 0 = 0$
The multiplication of two integers is an integer.
Example: $5 \times 5 = 25$
The order of the number does not matter when they are multiplied together.
Example: $25 \times 5 = 125$ or $5 \times 25 = 125$
If any number multiplied by 1 is equal to the original number.
Example: $5 \times 1 = 5$
Solved Example
Let's learn about multiplication by looking at solved examples based on 5-digit multiplication and 3-digit multiplication:
Q 1. Multiply 123 x 3
Ans: Step-1. Write the number one below the other as per the places of their digits.

Multiplication
Step-2. Multiply the ones digit of the top number by the ones digit of the bottom number.

Multiplication
Step-3. Multiply the tens digits of the top by the ones digit of the bottom number and you will get your answer.
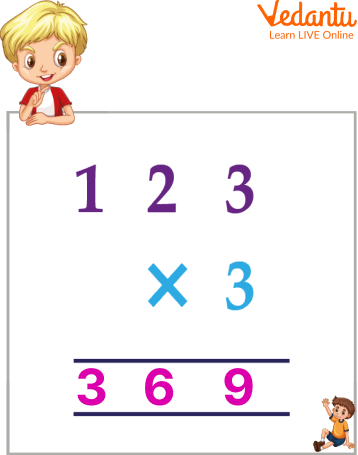
Multiplication
Q 2. Multiply 36953 x 3
Ans: Step-1. Write the number one below the other as per the places of the digit.
Step-2. Now by multiplying the tens place, if there is a carry of number, shift it to another number at the top of the hundreds place.
Step-3. By multiplying in this way, you will get your answer. i.e. 110859.

5-digit multiplication
Multiplication Practice Problems
Here are some practice problems based on hard multiplication:
Q 1. 343 x 213
Ans. 73,059
Q 2. 369 x 15
Ans. 5535
Q 3. 513 x 33
Ans. 16,929
3 Digit Multiplication Worksheets

3-Digit Multiplication Worksheets
Summary
So in this article, we learned about many wonderful things related to multiplication. We learned about multiplication, like what multiplication is and what are the symbols of multiplication. We learned the formula of multiplication. We also discussed the rules for multiplication to make hard multiplication easy.
We just did not end there. We also did some multiplication practice problems as we know that maths is not learned by reading. It's learned by solving by doing questions.
That's why we have provided a 3-digit multiplication worksheet to clear all your doubts.
FAQs on Multi Digit Multiplication Made Simple
1. What is multi-digit multiplication?
Multi-digit multiplication is the process of multiplying numbers that contain more than one digit. It involves breaking down the problem into smaller, simpler multiplication steps. In this process, a multiplicand (the number being multiplied) is multiplied by a multiplier (the number you multiply by) to find the final product.
2. How do you multiply multi-digit numbers step-by-step using the standard method?
The standard algorithm for multi-digit multiplication is a reliable way to solve these problems. For example, to multiply 45 by 23:
Step 1: Write the numbers vertically, aligning them by place value.
Step 2: Multiply the top number (45) by the ones digit of the bottom number (3). This gives you the first partial product: 45 × 3 = 135.
Step 3: Multiply the top number (45) by the tens digit of the bottom number (2), which represents 20. Place a zero in the ones place as a placeholder, then multiply: 45 × 20 = 900. This is your second partial product.
Step 4: Add the partial products together to get the final answer: 135 + 900 = 1035.
3. What are some different methods for multi-digit multiplication besides the standard algorithm?
Besides the standard method, students often learn other techniques to understand the concept better. Two common methods include:
The Grid Method (or Box Method): This visual method involves breaking down each number into its place value components (e.g., 45 becomes 40 and 5) and drawing a grid. You multiply the parts separately within the grid and then add all the results.
Lattice Multiplication: This is another visual method that uses a grid with diagonal lines. It separates the multiplication and addition steps, which can reduce errors for some learners.
4. Why is learning multiplication tables essential for mastering multi-digit multiplication?
Learning multiplication tables is crucial because they are the fundamental building blocks of multi-digit multiplication. Without knowing them by heart, each small step in a larger problem requires a separate calculation, which drastically slows you down and increases the chances of making mistakes. Strong knowledge of tables builds speed, accuracy, and confidence in solving complex maths problems.
5. What does 'carrying over' mean in multiplication, and why is it a crucial step?
Carrying over, or regrouping, is the process of moving a value from one place value column to the next. For instance, if multiplying the ones column gives you 15, you write down the 5 and 'carry over' the 1 to the tens column to be added later. This step is crucial because it ensures that the total value of each place is correctly accounted for. Forgetting to carry over is a common source of errors in multiplication.
6. How is multi-digit multiplication used in everyday situations?
Multi-digit multiplication is used frequently in real life. Some examples include:
Shopping: Calculating the total cost when buying multiple units of the same item, like 12 packets of biscuits costing ₹25 each.
Event Planning: Figuring out the total number of chairs needed for an event with 35 rows of 15 chairs each.
Budgeting: Calculating monthly or yearly expenses, such as finding the total amount spent on travel if a bus pass costs ₹475 per month for 12 months.
7. What is a simple trick to multiply two 2-digit numbers, for example, 23 x 14?
A simple trick is to use the distributive property to break down one of the numbers. To multiply 23 by 14, you can break 14 into (10 + 4). Then, the problem becomes easier to solve mentally:
First, multiply 23 by 10, which is 230.
Next, multiply 23 by 4, which is 92.
Finally, add the two results together: 230 + 92 = 322.
8. How does the standard multiplication method handle numbers with different numbers of digits, like 145 x 23?
The standard method works seamlessly even when the numbers have a different number of digits. You align the numbers to the right, regardless of their length. The process remains the same: you multiply the top number (145) by each digit of the bottom number (first by 3, then by 20), creating two separate partial products. You then add these partial products together to find the final answer. The structure of the algorithm automatically takes care of the correct place values.















