




Step-by-Step Guide to Solving Polynomial Division Problems
A generalised version of the well-known arithmetic operation known as long division, polynomial long division is an algorithm for dividing a polynomial by another polynomial of the same or lower degree in algebra. The long division method of polynomials is one of the most common methods of dividing polynomials. In this method, there is a divisor, a dividend (which is to be divided), a quotient, and a reminder. This is a very interesting method of dividing polynomials. The image given below describes the different terms used in the long division method of polynomials.
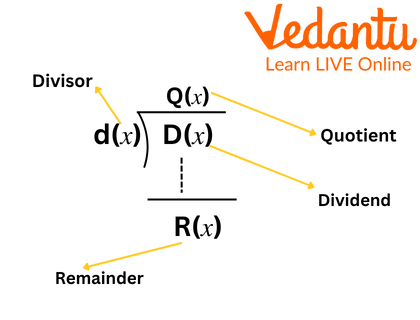
Polynomial Division
What is a Polynomial?
When exponents, constants and variables are combined using mathematical operations like addition, subtraction, multiplication and division, the result is a polynomial. The kind of the polynomial expression may be monomial, binomial or trinomial, depending on how many terms are included in it.
Example: \[9x,2x + 3y,3x + 4z - 9z + 5xyz\] and so on.
Monomial, Binomial and Trinomial
The number of terms in a polynomial determines which of three different sorts of polynomials it is. There are three different kinds of polynomials:
Monomial
Binomial
Trinomial
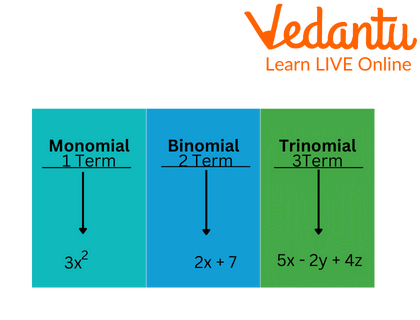
Types of Polynomials
Monomial
Monomial is an expression that contains only one member. There must be only one term which is nonzero. Here are some examples of monomials:
\[3x,5y\].
Binomial
A binomial expression is a polynomial expression containing exactly two terms. A binomial can be thought of as the sum or difference of two or more monomials. Here are some examples of binomials:
\[3x + 4y,6a + 5b\].
Trinomial
A trinomial is an expression with exactly three terms. Here are some examples of trinomial:
\[2{x^2} + 3x + 4\]
Long Division Method of Polynomial
Polynomial Division is the process of dividing one polynomial into another. You can perform division between different types of polynomials. Between two monomials, between a polynomial and a monomial, or between two polynomials. A polynomial is an n-algebraic expression with expressive variables, terms and coefficients.
Steps of Long Division Method of Polynomial
This method of Long Division Polynomials is as follows:
Sort the terms in descending order of degree.
Write the missing terms using 0 as the coefficient.
For the first term of the quotient, divide the first term of the dividend by the first term of the divisor.
Multiply this quotient by the divisor to get the product.
Subtract this product from the dividend and omit the next section (if any).
The difference and the shortened period form a new dividend.
Follow this process until you get the rest. The remainder can be zero or have an index less than the divisor.
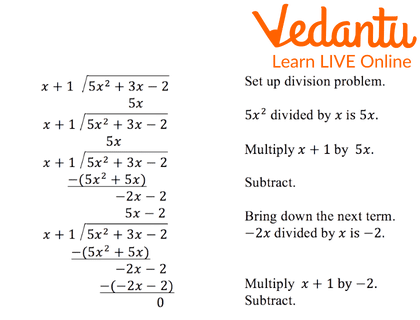
Long Division of Polynomials
Solved Examples on Division Polynomials
1. Solve \[\left( {24{x^2} + 2x + 4} \right) \div \left( {2x + 1} \right)\] using a long division method.
Ans: The image below will give a better understanding on how to divide Polynomials.

Answer: Remainder: 9
Quotient: 12x - 5
2. How are Polynomials Divided?
Ans: In mathematics, there are two ways to divide polynomials. These are the synthetic approach and lengthy division. The long division method is the most challenging and time-consuming to master, as its name suggests. The synthetic technique, on the other hand, is a "fun" way to divide polynomials.
FAQs on Long Division Method of Polynomials Explained
1. What is the long division method of polynomials?
The long division method of polynomials is a technique for dividing one polynomial by another, much like regular long division with numbers. It helps simplify expressions and find quotients and remainders using repeated subtraction and multiplication steps between the dividend and divisor polynomials.
2. Why do we use the long division method for polynomials?
We use the long division method for polynomials to break down complex polynomial expressions, simplify equations, and determine the quotient and remainder when dividing two polynomials. This method is especially useful in algebra for solving and factoring polynomial equations.
3. What are the steps involved in polynomial long division?
The key steps in polynomial long division are:
- Divide the leading term by the divisor's leading term.
- Multiply, subtract, and bring down the next term.
- Repeat until the remainder's degree is less than the divisor's degree.
4. Can you provide an example of dividing polynomials using the long division method?
To divide $x^2 + 3x + 2$ by $x + 1$, use the long division method to get: Quotient is $x + 2$, remainder is $0$. The process involves dividing the terms step by step, just as in arithmetic long division.
5. What do quotient and remainder mean in polynomial division?
In the long division of polynomials, the quotient is the polynomial that results from the division, while the remainder is what is left after the process. The relationship is written as: Dividend $=$ Divisor $ imes$ Quotient $+$ Remainder.
6. How do you know when to stop long division with polynomials?
During polynomial long division, you stop when the degree of the remainder is less than the degree of the divisor. At that point, no further division can occur and the last remainder is included in the final answer.
7. What is the purpose of aligning terms in polynomial long division?
Aligning terms in polynomial long division keeps like terms together, which makes the process organized and ensures correct subtraction and addition of polynomial terms. This helps prevent errors and allows each step to follow logically until the remainder is found.
8. Is synthetic division the same as polynomial long division?
No, synthetic division is a shortcut for dividing polynomials when the divisor is linear (of the form $x - a$). The long division method is a general technique used for any divisor, even if it's not linear.
9. What types of problems use long division of polynomials?
Long division of polynomials is used in
- simplifying complex rational expressions
- reducing fractions
- finding oblique asymptotes
- factoring higher-degree polynomials
10. Can the long division method find roots of a polynomial?
The long division method does not directly find roots of a polynomial, but it can be used to divide out a known root, simplifying the polynomial. After division, roots of the resulting factor can be found using other algebraic methods.
11. What should you do if the dividend is missing terms in long division?
If your dividend is missing terms in polynomial long division, insert zero coefficients for those missing degrees. For example, write $x^3 + 0x^2 + 4$ instead of $x^3 + 4$. This keeps terms aligned and makes calculations accurate.





















