




How to Solve Simplification Questions Quickly
In Mathematics, sometimes you get complicated sums and long calculations, which is very common in fraction questions. Some students find it more difficult and take a long time to solve. But don’t worry, this article on simplification in Maths has a resolution for you. It will help you to simplify the fractions in easy ways. In this article, you'll learn what simplification is, how to simplify fractions, and the steps involved in simplifying fractions. You'll also find out how to do it step by step.
What is Simplification?
As you know, simplification of mathematical problems helps increase scores in exams and is also used in daily life like in malls you get 35% discount, flat discount or 20% discount up to Rs 100. You only need to use fundamental simplification rules to solve equations in this part.
Thus, simplifying an expression implies employing different procedures to reduce it to a simpler version. The operations required to simplify things are done in a set order called BODMAS.
Where,
B = Bracket
0 = of
D = Division
M = Multiplication
A = Addition
S = Subtraction

Introduction to Simplification
To simplify a fraction, reduce it to its most basic form. If a fraction's numerator and denominator only share the number one, it is said to be in its simplest form. The process of simplifying difficulties as we work to tackle fractional problems is essential. The value of the fraction won't change even after we simplify them. This indicates that the true fraction and the simplified fraction are two equivalent fractions. We shall discover a few simple methods for simplifying fractions in this article.
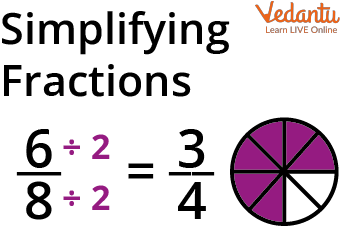
Simplifying Fractions
How to Simplify Fractions?
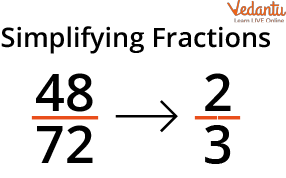
Simplify Fractions
Reducing a fraction to its simplest form is the definition of simplifying a fraction. If a fraction's numerator and denominator are coprime or share only the number one as a common factor, it is said to be in its simplest form. The given fraction is equal to the given fraction in its simplest form. For instance, the fraction $\dfrac{3}{4}$ is in its most basic form since the only element that 3 and 4 have in common is 1.
Let's attempt to gradually simplify the fraction $\dfrac{8}{24}$.
How to Simplify Fractions Step by Step?


How to Simplify Fractions Stepwise
Following is the process of how to simplify fractions step by step -
Step 1: Write the denominator and numerator's factors in step one.
The ratio between 8 and 24 is 1 through 8 factors: 2; 4; and 8
1, 2, 3, 4, 6, 8, 12, and 24 are the 24 factors.
Step 2: Verify the shared factors between the denominator and the numerator. 1, 2, 4, and 8 are the common factors of the numbers 8 and 24.
Step 3: Subtract the common components from the numerator and denominator until there is only one remaining.
The fraction that is so obtained is in its most basic form. Starting with a division of 2, $\dfrac{8}{24}$ becomes $\dfrac{\dfrac{8}{2}}{\dfrac{24}{2}}=\dfrac{4}{12}$.
Up until the point where we can no longer divide by 2, we will keep doing so. Thus, $\dfrac{\dfrac{4}{2}}{\dfrac{12}{2}}=\dfrac{2}{6}$, which is equal to $\dfrac{\dfrac{2}{2}}{\dfrac{6}{2}}=\dfrac{1}{3}$.
The fraction $\dfrac{8}{24}$ is thus represented by its simplest form, $\dfrac{1}{3}$.
Let's return to the original issue of how to make the fraction $\dfrac{8}{24}$ simpler. Between 8 and 24, 8 is their largest common factor. The simplest form of the fraction, which is $\dfrac{1}{3}$, can be obtained by immediately dividing the numerator, 8, by the denominator, 24, and vice versa.
How to Simplify Numbers

How to Simplify Numbers
Following is the way how to simplify numbers-
Round it Off.
Produce zeros. 200, therefore, becomes 199.
Round to an Order of Magnitude.
To the nearest "power of 10," round a lot. The result is that 218 becomes 100 and 2,180 becomes 1,000.
Slide the Decimal Point.
Rounding zeros are compacted by sliding the decimal point.
This makes 200,000,000 into 2 x 108. (exponential notation).
Replace it with a Number You Can Recall.
Find a nearby number that you can remember rather than rounding.
Thus, 218 can be easily converted to 222, 210, 200, or any number.
Solved Examples
Example 1: Simplify: $660 \div 22 \times(2+1)$
Ans: $660 \div 22 \times(2+1)$ (Solve parentheses first)
$=(660 \div 22) \times 3 \text { (From left to right, division appears first) }$
$=30 \times 3=90$
Example 2: Simplify: 37 − [28 + (19 − 7)]
Ans: $37-[28+(19-7)]$ First solve ( )
$=37-[28+12]$ Next, solve []
$=37-40$
$=77$
Practice Time
Q1. Simplify the expression: $4+(3 \times 4) \div 2$
Ans: 10
Q2. Simplify fractions: (i) $\dfrac{124}{136}$
(ii) $\dfrac{182}{192}$
Ans: (i) $\dfrac{31}{34}$
(ii) $\dfrac{91}96{}$
Conclusion
Simplification of expressions means rewriting the same algebraic expression with no like terms and in a compact manner. Making something simpler is making it less complex. When you describe a complex mathematical idea to a child in words they can easily understand, you are simplifying.
FAQs on Simplification in Maths: Complete Guide
1. What is simplification in mathematics?
Simplification in mathematics means making an expression or equation easier to work with by
- combining like terms
- removing brackets
- reducing fractions
2. Why is simplification important in solving math problems?
Simplification is important because it helps make math problems easier to solve. This process
- reduces calculation steps
- prevents mistakes
- helps clearly see patterns
3. How do you simplify expressions with brackets?
To simplify expressions with brackets, first remove the brackets by using rules like the distributive property. Then, combine like terms where possible. For example, $2(x + 3) = 2x + 6$. This makes the expression easier to evaluate.
4. What steps are involved in simplifying algebraic expressions?
To simplify algebraic expressions, follow these steps:
- Expand brackets
- Combine like terms
- Simplify coefficients
5. Can simplification involve fractions and decimals?
Yes, simplification often involves reducing fractions to their lowest terms or converting decimals into simpler forms. For instance, $\frac{6}{8}$ simplifies to $\frac{3}{4}$ by dividing by a common factor. This process makes calculations faster and clearer.
6. What is a like term in simplification?
Like terms are terms in an expression that have the same variable raised to the same power. For example, $3x$ and $5x$ are like terms, so they can be added together. Simplifying expressions often involves combining these terms.
7. How do you simplify an expression with exponents?
To simplify expressions with exponents, apply exponent rules such as $a^m \times a^n = a^{m+n}$. For example, $x^2 \times x^3 = x^5$. Always combine exponents with the same base whenever possible to simplify complex expressions.
8. What is the difference between simplification and solving?
Simplification means rewriting expressions in a simpler form, while solving involves finding the value of a variable. For example, simplifying $2x + 3x$ gives $5x$, while solving $5x = 10$ leads to $x = 2$.
9. Are there common mistakes to avoid when simplifying?
Yes, common mistakes include
- forgetting to combine like terms
- ignoring signs (plus or minus)
- misapplying exponent laws
10. How can simplification help in competitive exams?
In competitive exams, simplification saves time by reducing lengthy problems to manageable bits. It helps you avoid calculation errors, increases speed, and lets you focus on solving other challenging questions, improving your overall test performance and confidence.
11. What strategies can improve simplification skills?
To improve simplification skills:
- Practice regularly
- Learn and use math rules accurately
- Work on speed and accuracy
- Break complex expressions into smaller parts





















