




How to Identify, Visualize & Solve Problems on Pentagonal Pyramids
What Is A Pentagonal Pyramid?
In Geometry, a pentagonal pyramid is a pyramid with a pentagonal base and five triangular faces that meet at a point known as the apex. The regular pentagonal pyramid has a base that is pentagonal in shape and lateral faces that are equilateral triangles. It is one of the Johnsons solid.
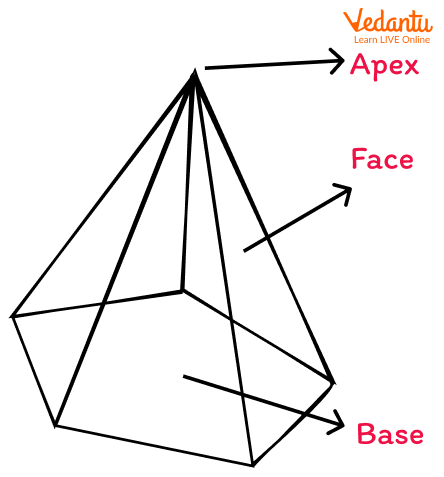
Pentagonal Pyramid
What are the Properties of a Pentagonal Pyramid?
The following are the properties of a pentagonal pyramid.
It has 6 faces.
The five side faces are triangular in shape.
The base is a pentagon.
It has 6 vertices.
It has 10 edges.
A pentagonal pyramid can also have an isosceles triangle (Triangle with two sides of equal length) as its lateral sides or lateral faces.
What is the Volume of the Pentagonal Pyramid?
The volume of a pentagonal pyramid is defined as the total space occupied by the pyramid in the three-dimensional space. The volume of a pentagonal pyramid is measured in cubic units.
The volume of any pyramid is calculated by multiplying the area of its base by its height and dividing the product by 3. Therefore, the volume of pyramid is given as,
Volume: 13 Base Area Height
As pentagonal pyramid has pentagonal base, therefore, the area of pentagon is calculated as:
Area = 1.72l²
Here, l is the length of one side of a pentagon.
The above formula for the area of the pentagon is calculated by dividing the pentagon into 5 triangles and finding the area of each triangle separately.
Therefore, the volume of pentagonal pyramid using the above expression for the area of given pentagon is calculated as:
Volume =1.72 3l²h
Here, l is the length of the one side of a pentagonal base and h is the height of the pyramid.
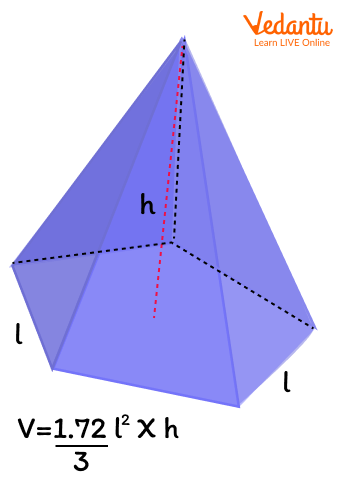
Volume of pentagonal pyramid
Let us understand the volume of the pentagonal pyramid with an example.
Example:
Find the volume of the pyramid with a pentagonal base 1 m and height 3 m.
Solution:
Pentagonal base : 1 m
Height of pentagon: 3 m
Now, we will use the volume of pentagonal pyramid formula with these values:
V = 1.72 31² 3
V = 1.72 3 3
V = 1.72
Hence, the volume of pentagonal pyramid with base length (1 m) and height (3 m) is given as 1.72m³.
What is the Surface Area of the Pentagonal Pyramid?
The surface area of a pentagonal pyramid is the entire surface occupied by the pyramid in three-dimensional space. The surface area of a pentagonal pyramid is measured in square units.
The surface area of any pyramid is calculated by adding the area of all the faces of the pyramid. Pentagonal pyramid has one pentagonal base and 5 triangular faces, and we used the following formula to calculate the area of the pentagonal face.
Area = 1.72l²
Here, l is the length of one side of the pentagonal base.
On the other hand, the area of triangle faces of pyramid is calculated by using the formula for area of triangle:
A = 12 Base Height
The five triangular faces of the pentagonal pyramid are congruent ( Congruent triangles have the same shape and same size).. Accordingly, the surface area of pentagonal pyramid is calculated as:
Surface Area of Pentagonal Pyramid Formula (AS) : 1.72l² + 52bh
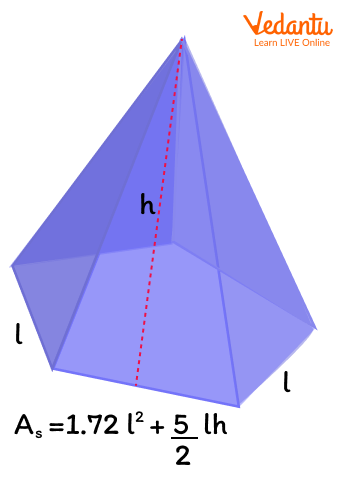
Surface area of pentagonal pyramid
Let us understand with an example.
Example:
Find the surface area of a pentagonal pyramid with height 5 m and side length 1 m?
Solution:
Height = 5 m
Length = 1 m
Now, we will use these values in the surface area of pentagonal pyramid formula:
(AS) : 1.72l² + 52bh
(AS) : 1.72(1)² + 52(1)(5)
(AS) : 1.72(1)² + 12.5
(AS): 14.22
Therefore, the surface area of the pentagonal pyramid is equal to 14.22 m².
In short, a three-dimensional shape with a pentagonal base and five triangular faces meeting is termed the pentagonal pyramid. As you have understood what a pentagonal pyramid is. Now, you can easily solve and practice sums based on the volume and surface area of the pentagonal pyramid using the formula discussed above.
FAQs on Pentagonal Pyramid: Key Concepts, Formulas, and Real-Life Examples
1. What are the key properties of a pentagonal pyramid in terms of its faces, edges, and vertices?
A pentagonal pyramid is a three-dimensional shape with specific properties. It has:
6 Faces: It includes one pentagonal base at the bottom and five triangular faces on the sides that meet at a single point.
10 Edges: There are five edges forming the perimeter of the pentagonal base, and five more edges connecting the base's vertices to the top point (apex).
6 Vertices: It has five vertices on the base (the corners of the pentagon) and one vertex at the top, known as the apex.
2. What are the formulas for calculating the volume and surface area of a pentagonal pyramid?
The two primary formulas for a pentagonal pyramid are for its volume and total surface area. They are:
Volume (V): The formula is V = (1/3) × Base Area × Height. The base area is the area of the pentagon.
Total Surface Area (TSA): The formula is TSA = Base Area + (1/2) × Perimeter of Base × Slant Height. This calculates the area of the pentagonal base plus the combined area of the five triangular faces.
3. What is the 'net' of a pentagonal pyramid and what does it look like?
The net of a pentagonal pyramid is a two-dimensional pattern that can be folded to form the 3D pyramid. It consists of two main parts: one pentagon, which serves as the base, and five triangles attached to each side of the pentagon. When you fold these triangles up so their top points meet, you create the pyramid's apex and its lateral faces.
4. What is the main difference between a pentagonal pyramid and a pentagonal prism?
The main difference lies in their top structure and side faces. A pentagonal pyramid has one pentagonal base and its side faces are triangles that meet at a single point (apex). In contrast, a pentagonal prism has two identical pentagonal bases (a top and a bottom) and its side faces are rectangles, connecting the corresponding edges of the two bases.
5. Where can we find examples of pentagonal pyramids in real life?
While less common than square pyramids, pentagonal pyramids can be found in various real-world contexts. Examples include:
Architecture: Some modern buildings or pavilions use a pentagonal pyramid shape for their roofs or structural design to create a unique aesthetic.
Decorative Items: You can find pentagonal pyramids in paperweights, crystal ornaments, or as parts of complex jewellery designs.
Chemistry: In molecular geometry, some molecules can have a pentagonal pyramidal shape, where a central atom is bonded to five atoms in a plane and one atom above it.
6. Why are the triangular faces of a 'regular' pentagonal pyramid always isosceles?
In a regular pentagonal pyramid, the base is a regular pentagon (all sides are equal), and the apex is located directly above the centre of the base. Because the apex is equidistant from all vertices of the base, the slanted edges connecting the apex to the base vertices are all of equal length. Each triangular face is formed by one side of the base and two of these equal-length slanted edges. A triangle with two equal sides is, by definition, an isosceles triangle.
7. How does Euler's formula apply to a pentagonal pyramid?
Euler's formula for polyhedrons states that V - E + F = 2, where V is the number of vertices, E is the number of edges, and F is the number of faces. For a pentagonal pyramid:
V = 6 (vertices)
E = 10 (edges)
F = 6 (faces)
Plugging these values into the formula: 6 - 10 + 6 = 2. Since the equation holds true, it confirms that the pentagonal pyramid is a valid convex polyhedron that follows this fundamental geometric rule.















