




How to Apply the Intercept Theorem in Maths Problems
The Intercept Theorem is a fundamental tool of Euclidean Geometry. The concept of parallel lines and transversal is of great importance in our day-to-day life. And, the Intercept theorem extends our understanding of parallel lines and transversal and we can apply these concepts in our day-to-day life.

A Transversal
In the above figure, we can see that there are 3 parallel lines ${L}_{1}$,${L}_{2}$, ${L}_{3}$ and then there is a transversal $PR$ which is intersecting all the 3 parallel lines at an equal distance. The intercept theorem, also known as Thale’s theorem, Basic Proportionality Theorem, or side splitter theorem, is an important theorem in elementary geometry about the ratios of various line segments that are created if two intersecting lines are intercepted by a pair of parallels.
History of the Mathematician

Euclid
Year of Birth: 325 BC
Year of Death: 270 BC
Contribution: He contributed significantly in the field of Mathematics and Physics by discovering the intercept theorem.
Statement of the Theorem
If there are three or more parallel lines and the intercepts made by them on one transversal are equal, the corresponding intercepts of any transversal are also equal.
Proof of the Theorem

Two Parallel Lines
Given:
$l$, $m$, $n$ are three parallel lines.
$P$ is a transversal intersecting the parallel lines such that $AB=BC$.
The transversal $Q$ has the intercepts $DE$ and $HE$ by the parallel lines $l$, $m$, $n$.
To prove:
$DE=EF$
Proof:
Draw a line $E$ parallel to the line $P$ which intersects the line $n$ at $H$ and line $l$ at $G$.
$AG||BE$ (Given)
$GE||AB$ (By construction)
From the information above, we can say that $AGBE$ is a parallelogram.
According to the properties of a parallelogram:
$AB=GE$ - (1)
Similarly, we can say that $BEHC$ is a parallelogram.
$BC=HE$ - (2)
From the given information, we know that $AB=BC$.
So, from equations (1) and (2), we can say that $GE=HE$.
In $\Delta GED$ and $\Delta HEF$,
$GE=HE$(Proved)
$\angle GED=\angle FEH$(Vertically Opposite Angles)
$\angle DGE=\angle FHE$(Alternate Interior Angles)
Hence, $\Delta GED\cong \Delta HEF$
As$\Delta GED\cong \Delta HEF$, the sides$DE=EF$.
Hence proved.
Applications of the Theorem
The intercept theorem can be used to prove that a certain construction yields parallel line segments:
If the midpoints of two triangle sides are connected, then the resulting line segment is parallel to the third triangle side (Mid point theorem of triangles).
If the midpoints of the two non-parallel sides of a trapezoid are connected, then the resulting line segment is parallel to the other two sides of the trapezoid.
Limitations of the Theorem
The intercept theorem is not able to help us in finding the midpoint of the sides of the triangle.
The basic proportionality theorem is an advanced version of the intercept theorem and it gives us a lot of information on the sides of the triangles.
Solved Examples
1. In a \[\Delta ABC\], sides \[AB\] and \[AC\] are intersected by a line at \[D\] and \[E\], respectively, which is parallel to side \[BC\]. Prove that \[\dfrac{AD}{AB}=\dfrac{AE}{AC}\].
Ans:

Scalene Triangle
\[DE||BC\] (Given)
So, \[\dfrac{AD}{DB}=\dfrac{AE}{EC}\]
Interchanging the ratios,
\[\dfrac{DB}{AD}=\dfrac{EC}{AE}\]
Adding 1 to both sides,
\[\dfrac{DB}{AD}+1=\dfrac{EC}{AE}+1\]
\[\dfrac{AD+DB}{AD}=\dfrac{EC+AE}{AE}\]
\[\dfrac{AB}{AD}=\dfrac{AC}{AE}\]
Interchanging the ratios again,
\[\dfrac{AD}{AB}=\dfrac{AE}{AC}\]
Hence proved.
2. Find DE
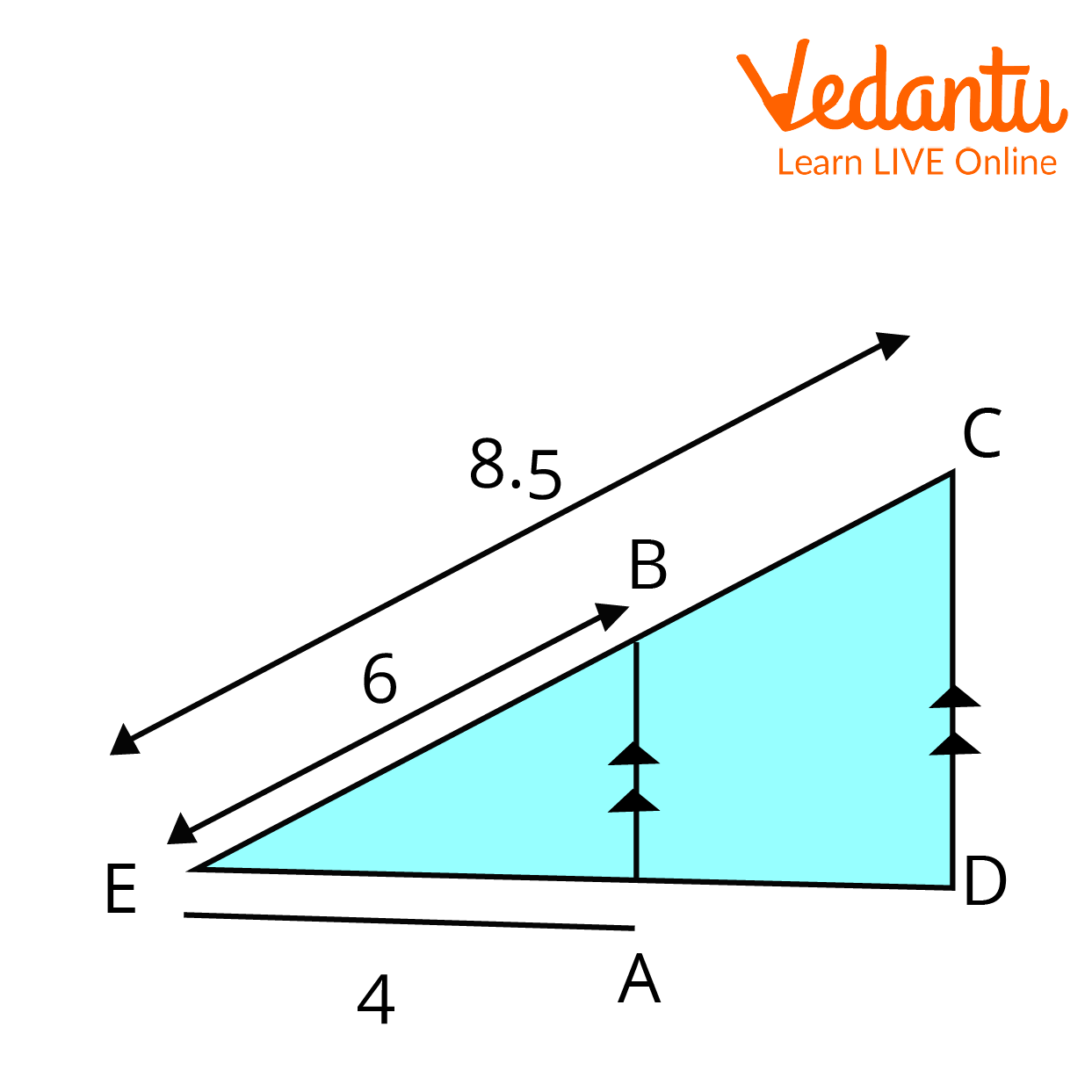
Basic Proportionality Theorem
Ans: According to the basic proportionality theorem,
\[\dfrac{AE}{DE}=\dfrac{BE}{CE}\]
\[\dfrac{4}{DE}=\dfrac{6}{8.5}\]
\[\dfrac{4*8.5}{6}=DE\]
\[DE=5.66\]
So, \[DE=5.66\]
3. In \[\Delta ABC\], \[D\] and \[E\] are points on the sides \[AB\] and \[AC\], respectively, such that \[DE||BC\]. If \[\dfrac{AD}{DB}=\dfrac{3}{4}\] and \[AC=15cm\], find \[AE\].

Intercept Theorem
Ans:\[\dfrac{AD}{DB}=\dfrac{AE}{EC}\] (According to the intercept theorem)
Let \[AE=x\] and \[EC=15-x\]
\[\dfrac{AD}{DB}=\dfrac{3}{4}\] (Given)
So, \[\dfrac{3}{4}=\dfrac{x}{15-x}\]
\[3(15-x)=4x\]
\[45=7x\]
\[x=\dfrac{45}{7}\]
\[x=6.4cm\]
So, \[x=6.4cm\]
Important Points
The intercept theorem can only be applied when the lies are parallel, if the transversal is cutting lines that are not parallel, then the intercept theorem is not valid.
The basic proportionality theorem and mid-point theorem are all applications of the intercept theorem but they are not the same theorems.
Conclusion
In the above article, we have discussed the Equal intercept Theorem and its proof. We have also discussed the applications of the theorem. So, we can conclude that Intercept Theorem is a fundamental tool of Geometry and is based on applications of parallel lines and transversal and reduces our computational work based on its application as we have seen in the examples based on the theorem.
FAQs on Intercept Theorem Explained for Students
1. What is the Intercept Theorem in Maths?
The Intercept Theorem, often related to the Basic Proportionality Theorem (BPT), is a key principle in geometry. It describes what happens when a set of parallel lines intersects two other lines, known as transversals. The theorem essentially states that the parallel lines will divide the two transversal lines into segments that are proportional to each other.
2. What is the official statement of the Intercept Theorem?
The Intercept Theorem states that if three or more parallel lines make intercepts on one transversal, they will make proportional intercepts on any other transversal that cuts them. For example, if parallel lines l, m, and n are intersected by transversals p and q, creating intercepts AB and BC on p, and DE and EF on q, then the ratio AB/BC = DE/EF holds true.
3. What is the formula or ratio derived from the Intercept Theorem?
The core formula of the Intercept Theorem is a statement of proportion. In the context of a triangle (where it is known as the Basic Proportionality Theorem), if a line DE is drawn parallel to side BC of a triangle ABC, intersecting sides AB and AC at points D and E respectively, the formula is: AD/DB = AE/EC. This shows that the line DE divides the two sides proportionally.
4. How is the Intercept Theorem different from the Basic Proportionality Theorem (BPT) and the Mid-point Theorem?
These three theorems are hierarchically related but apply to different scenarios:
- Intercept Theorem: This is the general version. It applies to any set of three or more parallel lines and any two transversals. It is not restricted to triangles.
- Basic Proportionality Theorem (BPT): This is a specific application of the Intercept Theorem to a triangle. It involves only one line drawn parallel to a side of the triangle.
- Mid-point Theorem: This is a special case of the BPT. Here, the line segment joins the exact mid-points of two sides, meaning the ratio of division is 1:1. It concludes the line is parallel to the third side and half its length.
5. Why is it essential for the lines to be parallel for the Intercept Theorem to apply?
The condition of parallel lines is non-negotiable because the proof of the Intercept Theorem relies on creating similar triangles. When parallel lines cut across transversals, they form triangles whose corresponding angles are equal (due to properties like corresponding angles and alternate interior angles). This equality of angles makes the triangles similar, which in turn guarantees that their corresponding sides are in proportion. Without parallel lines, this geometric similarity is lost, and the proportional relationship breaks down.
6. Where is the Intercept Theorem used in real-world examples?
The Intercept Theorem is fundamental to any field requiring scaling and proportional reasoning. Key examples include:
- Architecture and Engineering: Used to create scaled-down blueprints and models. It ensures that features like sloped roofs, support structures, and road alignments maintain correct proportions.
- Art and Design: Artists implicitly use this theorem to create realistic perspective in drawings, making objects appear larger or smaller with distance while maintaining their shape.
- Surveying and Cartography: Used by surveyors to determine large, inaccessible distances by measuring smaller, proportional distances on a baseline.
7. Is there an 'Intercept Theorem' specifically for circles?
While there isn't a theorem named 'Intercept Theorem' for circles, a similar concept of proportional segments exists in the Intersecting Secants Theorem. This theorem relates the lengths of the segments created when two secant lines intersect outside a circle. It establishes a product-based equality (not a ratio like the Intercept Theorem) between the external and total lengths of the secant segments. The underlying principles are different as it relies on the properties of circles, not parallel lines.
8. What is the statement and importance of the Converse of the Intercept Theorem?
The Converse of the Intercept Theorem provides a method to prove that lines are parallel. It states that if a line divides any two sides of a triangle in the same ratio, then the line must be parallel to the third side. Its importance lies in its utility; while the original theorem helps find side lengths when lines are known to be parallel, the converse helps prove that lines are parallel when side lengths are known.
























