




Essential Geometry Terms and Problem-Solving Strategies
Introduction
2D forms like triangles, squares, rectangles, and circles are examples of flat shapes in plane geometry. Solid geometry also refers to three-dimensional forms like cubes, cuboids, etc. as solids. Fundamental geometry is built on the coordinate geometry of points, lines, and planes. The area of mathematics known as geometry is concerned with the dimensions, sizes, forms, and angles of a wide range of common objects. Geometry comes from the Ancient Greek terms "geo" and "metron," which both imply "measuring." There are two-dimensional shapes and three-dimensional forms in Euclidean geometry.
Geometry's many sorts of forms make it easier for us to comprehend the shapes we encounter every day. Geometric ideas allow us to compute the area, perimeter, and volume of forms.
Basic Terms Used in Geometry are:
Line
Angle
Point
On a plane, a point is a particular area or position. Usually, a dot represents them. It's important to understand that a point is not an object, but rather a position. Remember that a point has just one location and, ideally, no dimensions.
Line
The line has no thickness, is straight (no curves), and goes in both directions without coming to an end (infinitely). It is significant to remember that an unlimited number of points come together to form a line.
Line Segment - A line is referred to as a Line Segment if it has a starting point and an ending point.
Ray - If there is a starting point and no ending point in a line then it becomes a ray.
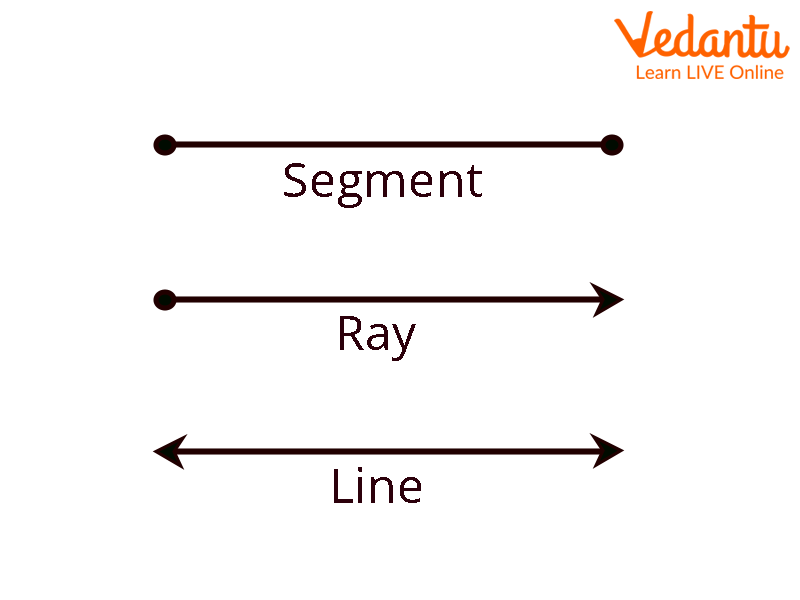
Line segment, Ray, Line
Class 5 Shapes and Angles
Two rays that share a termination and are collectively referred to as the angle's sides and vertices form an angle in planar geometry.
Acute Angle - A Acute angle is a smaller angle than a straight angle, i.e. It can be in the \[0^\circ \] to \[90^\circ \].
Obtuse Angle: Obtuse angles are those that are greater than \[90^\circ \] but less than \[180^\circ \].
Right Angle: A right angle is a \[90^\circ \]of angle.
Straight Angle - A straight angle is an angle created by a straight line, and it has a \[180^\circ \].
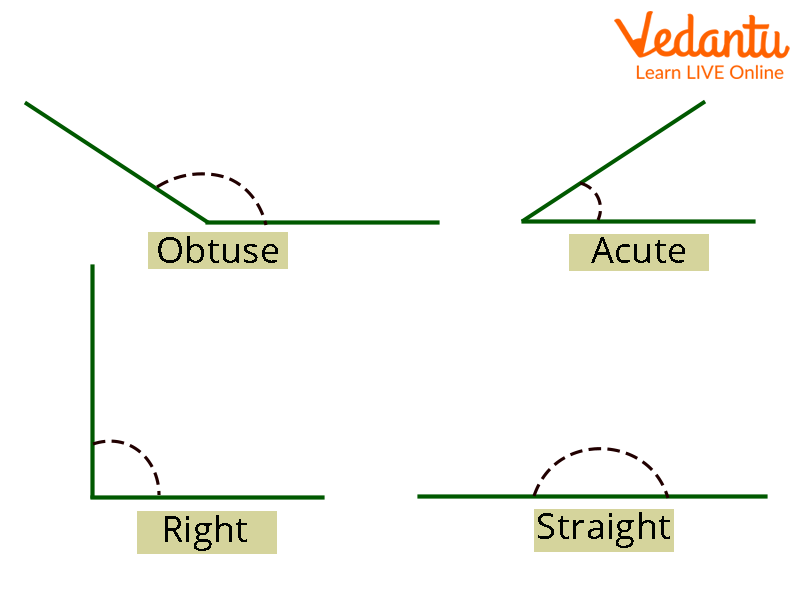
Angles
Basic Geometrical Figures and Shapes
Some basic geometrical figures are given below:
1. Triangle
The polygonal shape known as a triangle has three sides, three edges, and three vertices. Additionally, the total of its interior angles is \[180^\circ \].
2. Circle
A circle is a collection of all points that are all at the same set distance from a common central point.
3. Square
The quadrilateral known as the "square" has four equal sides and angles, and each of its vertices has a \[90^\circ \] angle.
4. Rectangle
The internal angles of a rectangle, which has four sides, are all exactly 90 degrees. At each corner or vertex, the two sides come together at a straight angle. The rectangle differs from a square because its two opposite sides are of equal length.
5. Polygon
A polygon is a closed, two-dimensional structure with straight line segments in mathematics. It does not have three dimensions. There aren't any curved surfaces in a polygon. A polygon must have three sides at a minimum. Only at its terminal must each side of a line segment cross another line segment.
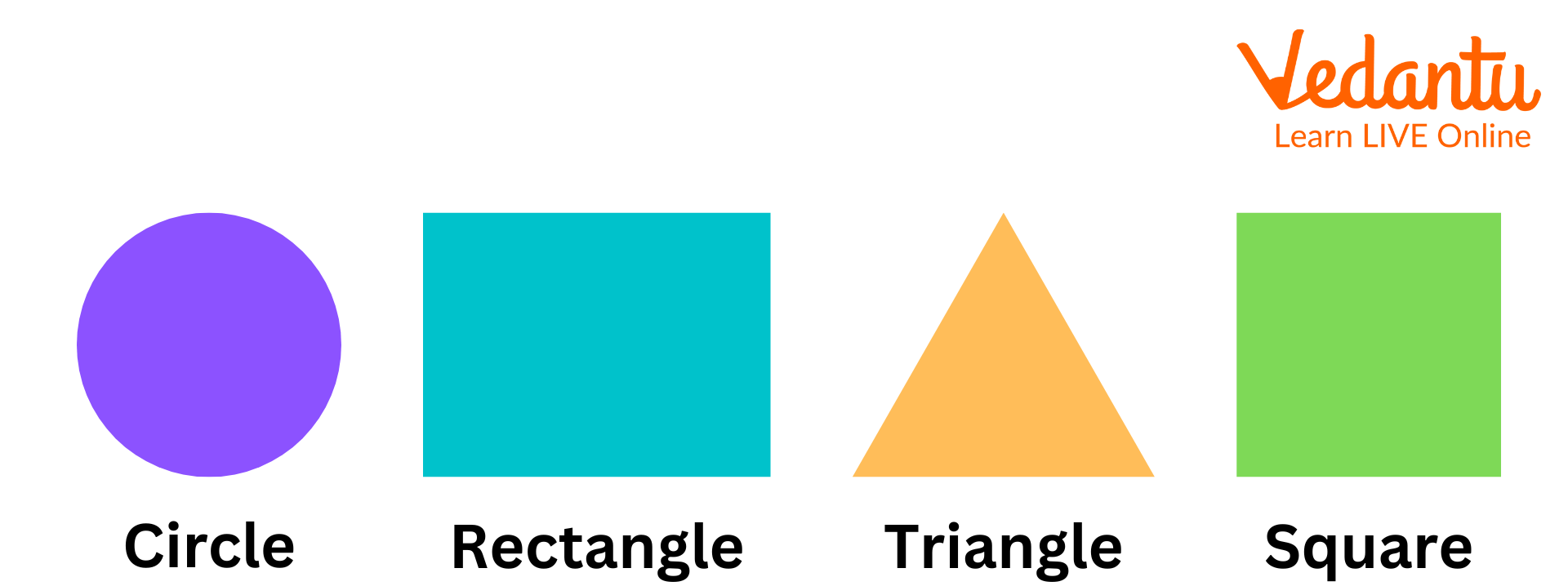
Different Geometrical Shapes
Conclusion:
Geometry is a branch of mathematics that focuses on measuring, describing, and relating points, lines, angles, surfaces, and solids. The four fundamental components of geometry are a point, a line, an angle, and a plane. Flat forms in plane geometry include 2-dimensional shapes including triangles, squares, rectangles, and circles. Three-dimensional forms like a cube, cuboid, cone, etc. are also referred to as solids in solid geometry. The coordinate geometry of points, lines, and planes is the foundation of fundamental geometry.
Solved Examples
1. What is the total angle of the triangle?
Ans: The Total of angles of a triangle is 180 degrees.
2. What kind of shape is a cone?
Ans: A cone is a solid, three-dimensional shape having a single vertex and a circular base. From the base to the vertex, the cone's surface narrows.
3. Give a few differences between a square and a rectangle.
Ans:
FAQs on Geometry for Class 5: Key Concepts and Examples
1. What are the basic concepts a Class 5 student learns in geometry?
In Class 5 geometry, students are introduced to the fundamental building blocks of shapes. These concepts include:
- Point: A single dot representing an exact location. It has no size.
- Line: A straight path of points that extends endlessly in both directions.
- Line Segment: A part of a line with two fixed endpoints. It has a definite length.
- Ray: A part of a line that starts at one endpoint and extends endlessly in one direction.
- Angle: Formed when two rays meet at a common endpoint, called the vertex.
2. What are the main types of angles taught in Class 5?
For Class 5 students, understanding angles is a key part of geometry. The main types of angles are classified by their measurement in degrees:
- Acute Angle: An angle that measures less than 90°.
- Right Angle: An angle that measures exactly 90°, like the corner of a square.
- Obtuse Angle: An angle that measures more than 90° but less than 180°.
- Straight Angle: An angle that measures exactly 180°, forming a straight line.
3. How is a 2D shape like a rectangle different from a 3D shape like a cuboid?
The main difference is in their dimensions. A 2D (two-dimensional) shape like a rectangle is flat and has only two dimensions: length and width. You can draw it on a piece of paper. A 3D (three-dimensional) shape like a cuboid is a solid object and has three dimensions: length, width, and height. It has faces (the flat surfaces), edges (where faces meet), and vertices (corners).
4. What is the difference between a line, a line segment, and a ray?
These three concepts are often confused but are distinct. A line has no endpoints and extends infinitely in both directions. A line segment is a finite part of a line with two fixed endpoints, meaning it has a measurable length. A ray has one fixed endpoint (its starting point) and extends infinitely in only one direction, much like a ray of sunlight from the sun.
5. How do we use the geometry we learn in Class 5 in our everyday lives?
Geometry is all around us! We use the concepts from Class 5 daily without even realising it. For example, when you read a clock, the hands form different angles (acute, obtuse, right). The floor tiles are often squares or rectangles. A slice of pizza is shaped like a triangle, and a cricket ball is a sphere. Understanding these shapes and angles helps us make sense of the world.
6. Why is it important for a Class 5 student to learn about geometry?
Learning geometry in Class 5 is crucial as it builds spatial reasoning skills. It helps a child understand and describe the world around them more accurately. This knowledge is the foundation for more advanced topics in maths and science. It also improves problem-solving abilities, creativity, and skills needed for activities like drawing, crafting, and even reading maps.
7. What does 'symmetry' mean in geometry, and can you give an example?
In geometry, symmetry means that a shape is made up of exactly similar parts facing each other or around an axis. If you can draw a line (called the line of symmetry) through a shape and fold it along that line so that both halves match perfectly, the shape is symmetrical. A perfect example is a butterfly; its left wing is a mirror image of its right wing.
8. How does a protractor help us understand different types of angles?
A protractor is a tool that does more than just measure an angle; it helps us classify it. By placing the protractor's baseline on one arm of the angle and its centre on the vertex, we can read the measurement in degrees. This number tells us exactly what type of angle it is: if the number is less than 90, it's an acute angle; if it's exactly 90, it's a right angle; and if it's more than 90, it's an obtuse angle. It turns an abstract shape into a precise measurement.















