




Key Strategies to Remember Multiplication and Division Facts
Multiplication and division are basic knowledge for school students. Multiplication is the process of calculating the product of two or more numbers. It is a basic arithmetic operation that is frequently used in everyday life. When we need to combine groups of equivalent size, we employ multiplication. Division is the separating of a large group into smaller groups so that each group has an equal number of things. In Mathematics, it is an operation used for equal grouping and equal sharing. In this article, we will introduce you to some well-known multiplication and division facts.
What are Multiplication and Division Facts?
The numbers that are being multiplied are referred to as factors, and the outcome of the multiplication is referred to as the product.
In division, the dividend is the number being divided, the divisor is the number dividing it, and the quotient is the outcome of the division.
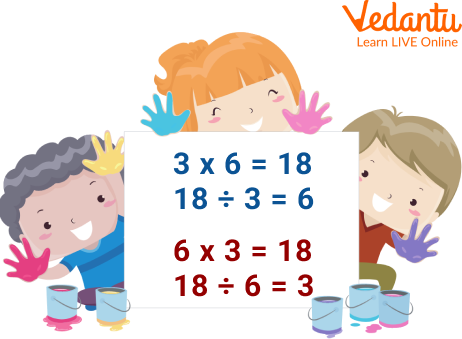
Multiplication and Division
Division and Multiplication-related Facts
You can write a multiplication fact simply by writing out a multiplication calculation. For example: 12 × 12 = 144, 3 × 6 = 18 and 8 × 5 = 40
You can also write multiplication facts using different methods of multiplication. For example, repeated addition is a way of finding multiplication facts by repeatedly adding a number until you reach the answer. 2 × 5 is the same as 2 + 2 + 2 + 2 + 2 = 10. The multiplication fact in that case is 10.
If the dividend is ‘zero’ then any number as a divisor will give the quotient as ‘zero’.
Example: If ‘zero’ sweets are to be distributed among 8 children, naturally no one will get any sweets.
If the divisor is ‘1’ then any dividend will have the quotient equal to itself.
Example: There are 15 sweets; each child is to get 1 sweet. How many children get sweets?

Division of 15 by 1
Multiplication and Division Drills
Q1. At a zoo, there are 45 deer. Find out the total number of legs of all the deer.
Ans: There are a total of 45 deer. We know that each deer will have 4 legs.
Therefore, the total number of legs deer will have will be equal to the:
$= 45 \times 4$
= 180.
Hence, 180 will be the total number of legs of all the deer.
Q2. Write two multiplication for each division:
(i) 15 ÷ 3 = 5
Ans: The two multiplication for it will be: 5 × 3 = 15 and 3 × 5 = 15
(ii) 3 ÷ 3 = 1
Ans: The two multiplication for it will be: 1 × 3 = 3 and 3 × 1 = 3
Practice Questions
Q1. Write two multiplication for each division:
(i) 21 ÷ 3 = 7
(ii) 30 ÷ 3 = 10
(iii) 33 ÷ 3 = 11
Ans:
(i) 7 × 3 = 21 and 3 × 7 = 21
(ii) 10 × 3 = 30 and 3 × 10 = 30
(iii) 11 × 3 = 33 and 3 × 11 = 33
Q2. Write two divisions for each multiplication:
(i) 6 × 3 = 18 (Ans: 18 ÷ 3 = 6 and 18 ÷ 6 = 3)
(ii) 2 × 3 = 6 (Ans: 6 ÷ 2 = 3 and 6 ÷ 3 = 2)
(iii) 9 × 3 = 27 (Ans: 27 ÷ 9 = 3 and 27 ÷ 3 = 9)
(iv) 12 × 3 = 36 (Ans: 36 ÷ 3 = 12 and 36 ÷ 12 = 3)
(v) 8 × 3 = 24 (Ans: 24 ÷ 3 = 8 and 24 ÷ 8 = 3)
Summary
In this article, we have learned about multiplication which is a mathematical operation that conveys the fundamental concept of repeated addition of the same integer. Later, we also learned about division sentences, as it is a basic mathematical operation in which a bigger number is divided into smaller groups with the same number of components. In the end, we have seen some practice problems based on the facts. We hope you have a clear picture of the facts on multiplication and division. Practise further to enhance your understanding of the topic.
FAQs on Essential Facts About Division and Multiplication
1. What are the main parts of a multiplication problem?
In a multiplication problem, the numbers have special names. For example, in 5 × 3 = 15, the terms are:
The first number (5) is the multiplicand.
The second number (3) is the multiplier.
The answer (15) is called the product.
Both the multiplicand and multiplier are also known as factors.
2. What are the essential terms to know in division?
When you divide, each part of the problem has a name. For instance, in 16 ÷ 4 = 4, the key terms are:
Dividend: The number that is being divided (16).
Divisor: The number you are dividing by (4).
Quotient: The result of the division (4).
If a number doesn't divide completely, the leftover part is called the remainder.
3. How are multiplication and division related to each other?
Multiplication and division are inverse operations, which means they are opposites that undo each other. If you know a multiplication fact, you can find two related division facts. For example, from the multiplication fact 6 × 4 = 24, you also know that 24 ÷ 4 = 6 and 24 ÷ 6 = 4. This group of related equations is often called a 'fact family'.
4. How can I use multiplication in my daily life?
You use multiplication in everyday situations, often without realising it. For example, if you want to buy 4 pencils that cost ₹5 each, you multiply 4 × 5 to find the total cost of ₹20. It's also used for calculating ingredients for a recipe, figuring out the total number of items in several groups, or determining the area of a room.
5. What are the basic properties of multiplication?
Multiplication has some simple rules, or properties, that make calculations easier:
Commutative Property: The order of numbers does not change the product (e.g., 2 × 8 is the same as 8 × 2).
Identity Property: Any number multiplied by 1 is the number itself (e.g., 9 × 1 = 9).
Zero Property: Any number multiplied by 0 is always 0 (e.g., 15 × 0 = 0).
6. Why is multiplication often explained as 'repeated addition'?
Multiplication is essentially a fast way of doing repeated addition. For instance, the expression 4 × 3 is a shortcut for adding the number 4 three times (4 + 4 + 4 = 12). Instead of adding the same number over and over, we can simply multiply to get the answer much more quickly, which is especially useful with larger numbers.
7. Why can you not divide a number by zero?
Dividing a number by zero is undefined in mathematics because it represents an impossible action. Division means splitting a quantity into a certain number of equal groups. If you have 10 cookies (the dividend) and you want to put them into 0 groups (the divisor), the task cannot be done. Furthermore, because division and multiplication are opposites, if 10 ÷ 0 = ? were possible, then ? × 0 would have to equal 10. However, any number multiplied by zero is always zero, so this is a contradiction.
8. How can you use multiplication to check if your division answer is correct?
Because multiplication and division are inverse operations, you can use one to verify the other. After you solve a division problem, you can check your work by multiplying the quotient (the answer) by the divisor. The result should equal your original dividend. For example, if you calculate that 56 ÷ 7 = 8, you can check it by multiplying 8 × 7. Since the product is 56, your division was correct.
9. What are the special rules for dividing a number by 1 or by itself?
There are two important rules about division that simplify calculations:
Dividing by 1: Any number divided by 1 is always the number itself. For example, 12 ÷ 1 = 12. This is because you are splitting the total amount into just one group.
Dividing by itself: Any number (except zero) divided by itself is always 1. For example, 12 ÷ 12 = 1. This is because you are splitting the number into groups equal to its value, so each group contains exactly one.















