How to Divide a Whole Number by a Decimal Step by Step with Examples
Dividing decimals is very much familiar to the division of whole numbers except for the decimal point. While dividing the decimal numbers, there are certain sets of rules which need to be followed but there are no changes in the basic process of the division. In Maths, decimals are referred to the specific types of numbers, with a whole number, and the fractional part is called the decimal point.
In this article, we are going to learn about how to divide decimals with whole numbers, how to divide decimals by whole numbers with remainders, what is the whole process and also going to solve divide decimals with whole numbers worksheets.
What is the Division of Decimals?
The division of decimals is similar to the division of the whole number and the whole process of the division. But in mind, we should be aware that the decimal point should be placed correctly in the quotient. A decimal number has a whole number part and a fractional part which is separated by a dot which is known as the decimal point. The digits after the decimal point carry a value that is smaller than 1.
For example, 34.15 is a decimal number in which 34 is the whole number part and 15 is the fractional part.
How to Divide Decimals with Whole Numbers Step by Step
There are certain rules for dividing the decimal in maths. In this paragraph, we are going to see how to divide decimals with whole numbers step by step:
Step 1: Write down the provided expression in the standard form of the division.
Step 2: Now, we need to divide the decimal number’s whole part by the divisor.
How to Divide Decimals With Whole Numbers Step By Step
Step 3: Then, put the decimal point in the quotient above the dividend’s decimal point and then bring down the tenth digit.
Step 4: If the tenth digits of the obtained dividend cannot be divided by the divisor, then write 0 in the quotient and front of the tenth digit. Or just proceed with the process of the division.
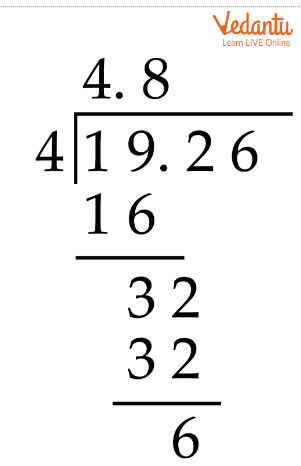
How To Divide Decimals With Whole Numbers Step By Step
Step 5: Lastly, keep repeating the steps and adding zeros in the dividend till 0 is obtained in the remainder.
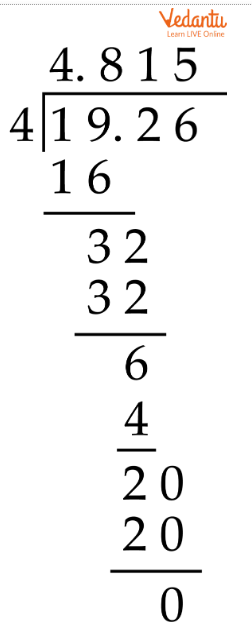
How To Divide Decimals With Whole Numbers Step By Step
Therefore, in the end, we got the outcome of 19.26 $\div$ 4 is 4.815. It indicates that the quotient is 4.815 and the remainder is 0.
Let us take another example of the division of decimals by whole numbers with remainder, as here the remainder is not going to be zero.
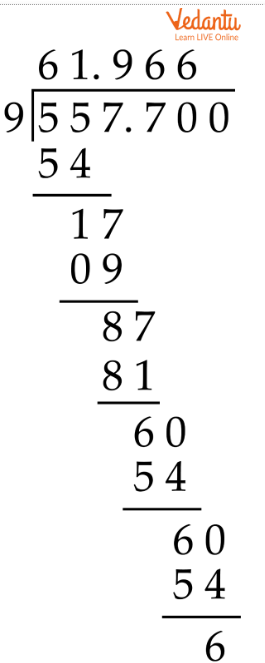
How To Divide Decimals By Whole Numbers With Remainder
Solved Examples of How to Divide Decimals by Whole Numbers with Remainders and Without Remainders
Q1. Divide 230.5 by 5.
Solution:
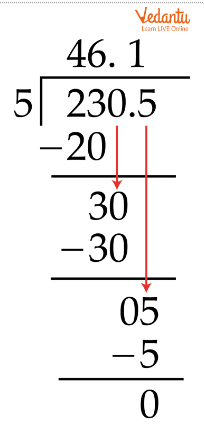
How To Divide Decimals By Whole Numbers With Remainder, Zero
So, the quotient is 46.1.
Q 2. Find out the quotient of $56.21 \div 10$
Ans:
How To Divide Decimals By Whole Numbers With Remainder
Thus the quotient is 5.62.
Practice Questions
Here, let’s see some practice questions to get clarity on how to divide decimals by whole numbers:
Q 1. $0.8 \div 4$
Ans: 0.2
Q 2. $6.8 \div 2$
Ans: 3.4
Q 3. $0.3 \div 3$
Ans: 0.1
Q 4. $2.4 \div 4$
Ans: 0.6
Q 5. $22.4 \div 4$
Ans: 5.6
Divide Decimals by Whole Numbers Worksheet
Dividing decimals by whole numbers worksheets are aimed at teaching the arithmetic basics. Practising a variety of division problems will help boost students' confidence in dealing with decimals and whole numbers.
Divide Decimals By Whole Numbers Worksheet
Divide Decimals By Whole Numbers Worksheet
Summary
In this article, we have learned and discussed how to find the quotient in the division of decimals by the whole number and also how to divide decimals by the whole number with the remainder. We are also going to practise dividing decimals by a whole numbers worksheet. We have also learned a stepwise process in detail with enough examples of how to solve the problems related to the division of decimals with whole numbers in a much easier way. In Mathematics, a familiar division approach (as we do for whole numbers) is also followed for decimals.
FAQs on Dividing a Whole Number by a Decimal
1. How do you divide a whole number by a decimal?
To divide a whole number by a decimal, move the decimal point in the divisor to make it a whole number and move it the same number of places in the dividend. Then divide as usual.
- Step 1: Identify the decimal in the divisor.
- Step 2: Move the decimal right until the divisor becomes a whole number.
- Step 3: Move the decimal in the dividend the same number of places.
- Step 4: Perform standard long division.
2. What is the rule for dividing a whole number by a decimal?
The rule for dividing by a decimal is to multiply both the dividend and divisor by the same power of 10 to make the divisor a whole number. This keeps the value of the division unchanged.
- If the divisor has 1 decimal place, multiply both numbers by 10.
- If it has 2 decimal places, multiply both by 100.
- Then divide normally.
3. Can you give an example of dividing a whole number by a decimal?
An example of dividing a whole number by a decimal is 35 ÷ 0.5 = 70. To solve:
- 0.5 has 1 decimal place, so multiply both numbers by 10.
- 35 × 10 = 350 and 0.5 × 10 = 5.
- Now divide: 350 ÷ 5 = 70.
4. Why do we move the decimal point when dividing by a decimal?
We move the decimal point to turn the divisor into a whole number, which makes the division simpler while keeping the value the same. Multiplying both numbers by the same power of 10 does not change the quotient.
- This uses the property of equivalent fractions.
- It converts decimal division into whole number division.
- It reduces calculation errors.
5. What happens when you divide a whole number by a decimal less than 1?
When you divide a whole number by a decimal less than 1, the answer is usually greater than the original whole number. This is because dividing by a number less than 1 increases the value.
- Example: 12 ÷ 0.4
- Multiply both by 10 → 120 ÷ 4
- Result = 30
6. How do you divide a whole number by a decimal using long division?
To divide a whole number by a decimal using long division, first convert the divisor to a whole number, then apply the long division steps. Follow these steps:
- Move the decimal in the divisor to make it whole.
- Move the decimal in the dividend the same number of places.
- Divide using standard long division.
7. What is 45 divided by 0.9?
45 divided by 0.9 equals 50. To calculate:
- 0.9 has one decimal place, so multiply both numbers by 10.
- 45 × 10 = 450 and 0.9 × 10 = 9.
- Now divide: 450 ÷ 9 = 50.
8. What are common mistakes when dividing a whole number by a decimal?
A common mistake when dividing a whole number by a decimal is forgetting to move the decimal in both numbers. Key errors include:
- Moving the decimal in the divisor but not in the dividend.
- Not multiplying by the correct power of 10.
- Placing the decimal incorrectly in the final answer.
9. Is dividing by 0.5 the same as multiplying by 2?
Yes, dividing by 0.5 is the same as multiplying by 2. This works because 0.5 is equal to 1/2, and dividing by 1/2 is equivalent to multiplying by 2.
- Example: 16 ÷ 0.5 = 16 × 2
- Result = 32
10. How do you check your answer when dividing a whole number by a decimal?
You can check your answer by multiplying the quotient by the original decimal divisor. If the result equals the original whole number, the division is correct.
- Example: 40 ÷ 0.8 = 50
- Check: 50 × 0.8 = 40
