




How to Convert Degrees to Radians: Step-by-Step Examples
How far is your school from your home? How much time do you take to reach your home? 10 km, and it will take 15 minutes by bicycle. And, how far is your best friend’s home from yours and how much time do you take to reach his home? Approximately 500 metres, and 2 to 3 minutes by walk. What do km or metre and minutes represent here? These are the units of distance and time, respectively. Do you know what is the unit to measure an angle?
The unit which is used to measure the angle is ‘degree’. In this article, we will dive deep into the definition of ‘degree’, its symbol, and its conversion into another unit. So waiting for what my dear child, let us go!
Definition of Degree
In Geometry, the unit which is used to measure the angle is known as 'degree'. There are other units also used to measure the angle, but the degree is most popular and commonly used amongst all. The other common unit used to measure the angle is ‘radian’. It is the SI unit to measure an angle. We can convert both units into one another using some formulas.
A protractor is used to measure the angles in degrees.
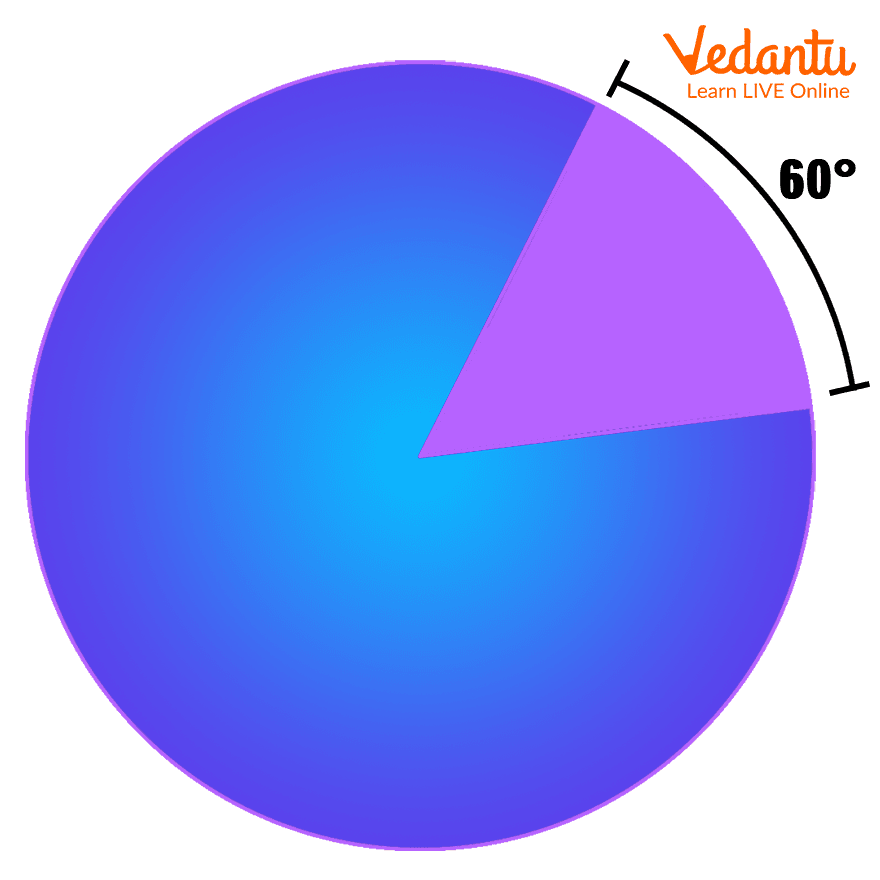
An example of ‘degree’; degree measure 60
Degree Symbol
A degree is represented by the symbol °. It is of the shape of a small circle that would be written after a number and on its top such as 0 degree = 0°, 90 degree = 90°, 180 degree = 180°, etc.
Types of Angles on the Basis of Their Degrees
There are different types of angles based on their measurement. Some of them are listed below:
Acute Angle: The angle which measures more than 0° and less than 90°, is called an acute angle.
Right Angle: The angle which measures 90° is called the right angle.
Obtuse Angle: The angle which measures more than 90° and less than 180°, is called the obtuse angle.
Straight Angle: The angle which measures exactly 180° is called a straight angle.
Reflex Angle: The angle which measures more than 180° and less than 360° is called a reflex angle.
Complete Angle: The angle which measures 360° is called a complete angle. A complete circle measures 360°.
Conversion of Units of Angle
There are mostly two units used to measure the angle, radian and degree. They both are interchangeable. Now let us see how to convert both of them.
Degree to Radian
To convert degree to radian, we use the following formula:
Radian = \[ \frac{angle \, in \, degree\times \Pi }{180^{0}} \]
Radian to Degree
To convert radian to a degree, we use the following formula:
Degree = \[ \frac{angle \, in \, radians \times 180^{0}}{\Pi} \]
Numerical Type Questions
1. Convert 45° into radian.
Solution: To convert degree to radian, we can calculate as:
Angle in radian = \[ \frac{angle \, in \, degree \times π}{180^{0}} \]
= \[ \frac{45^{0} \times \Pi}{180^{0}} \]
= \[ \frac{\Pi}{4} \]
2. A child measures an angle of 2𝜋 radian. Convert it to the degree.
Solution: To convert radian to degree, we can calculate as:
Angle in degree = \[ \frac{angle \, in \, radians \times 180^{0}}{\Pi} \]
= \[ \frac{2\Pi \times 180^{0}}{\Pi} \]
= \[ 180^{0} \]
Points to Remember
1. If θ is the measured angle, then we can remember the names of the angles and their measurement as:
2. A protector can measure the angle in two ways:
Clockwise direction
Anti-clockwise angle
FAQs on What Is a Degree in Math? Definition, Symbol & Conversion Guide
1. What is the basic definition of a degree in mathematics?
In geometry, a degree (denoted by the symbol °) is the standard unit used to measure plane angles. A full circle or one complete rotation is defined as having 360 degrees. Therefore, one degree (1°) represents 1/360th of a full rotation. This system is widely used in fields like construction, navigation, and astronomy for its practical simplicity.
2. How are the main types of angles classified using degrees?
Angles are classified based on their measurement in degrees. The primary types are:
- Acute Angle: An angle that measures more than 0° but less than 90°.
- Right Angle: An angle that measures exactly 90°.
- Obtuse Angle: An angle that measures more than 90° but less than 180°.
- Straight Angle: An angle that measures exactly 180°.
- Reflex Angle: An angle that measures more than 180° but less than 360°.
- Complete Angle: An angle that measures exactly 360°.
3. What are some real-world examples where measuring angles in degrees is important?
Measuring angles in degrees is crucial in many practical applications. For instance, in construction and architecture, builders use degrees to ensure walls are perpendicular (90°) and roofs have the correct slope. In navigation, pilots and sailors use degrees of latitude and longitude to plot their course. Similarly, astronomers use degrees to locate celestial objects in the sky.
4. How is the 'degree' used for measuring angles different from the 'degree' of a polynomial in algebra?
This is a common point of confusion. The two concepts are completely different:
- The degree of an angle is a unit of measurement for rotation or the space between two intersecting lines, fundamental to geometry and trigonometry.
- The degree of a polynomial is the highest exponent of the variable in any term of that polynomial, which is a key concept in algebra. For example, in the polynomial x³ + 2x - 5, the degree is 3.
5. Why is a full circle divided into 360 degrees and not a simpler number like 100?
The choice of 360 degrees for a full circle dates back to the ancient Babylonians. The number 360 is highly convenient because it is divisible by many numbers (1, 2, 3, 4, 5, 6, 8, 9, 10, 12, 15, 18, 20, 24, 30, 36, 40, 45, 60, 72, 90, 120, 180), making it easy to divide a circle into smaller, equal parts without using fractions. This was particularly useful for their astronomical calculations and calendar systems.
6. How do you convert degrees to radians, and when is it better to use radians?
Degrees and radians are two different units for measuring angles. The key conversion formula is π radians = 180°. To convert from degrees to radians, you multiply the angle by (π/180). While degrees are common in everyday applications, radians are preferred in higher-level mathematics, especially in calculus and trigonometry, because they simplify formulas involving trigonometric functions and their derivatives.
7. Can a degree be broken down into smaller units?
Yes, for very precise measurements, a degree can be subdivided. One degree is equal to 60 minutes (denoted by '), and one minute is equal to 60 seconds (denoted by ″). This system is similar to how time is divided and is commonly used in fields like cartography and navigation for specifying geographic coordinates with high accuracy.















