




Step-by-Step Solutions to Common Area Questions
We all are aware of what squares are and how to find the area of a square. But in area word problems on the topic square, we will find the area in which the four sides are given as equal. To find the area of a given square, we must ensure that the sides of the square are in the same unit of length. In case they are given in different units, change them to the same unit. Some area of square examples is given to better understand the topic.
What is a Square?
A regular quadrilateral in which all four sides are of equal length and all four angles are equal is considered a square. The angles of the square are 90 degrees each. Also, the square's diagonals are equal and bisect each other at 90 degrees.
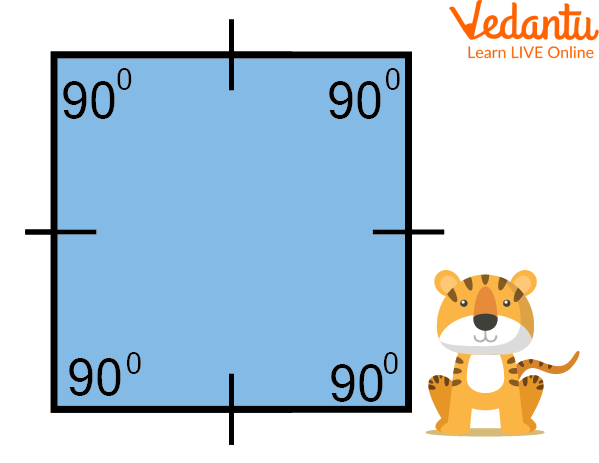
A Square
The above figure represents a square in which all the sides are equal, and each angle is 90 degrees.
Similarly, a parallelogram with all of its two adjacent sides being equal with one right vertex angle is a square.
Properties of a Square
The properties of a square are listed below:
All the interior angles are equal to 90°
All the sides of the square are equal and congruent with each other
The opposite sides of the square are always parallel to each other
The diagonal of the square divides it into similar isosceles triangles
The length of diagonals is always greater than the sides of the square
The square’s diagonals bisect each other at 90°
Both diagonals of the square are equal to each other
The square contains 4 vertices and 4 sides
Area of Square Formula
Since we know that a square is a shape which has four equal sides and every angle is a right angle, i.e. 90°. And hence, the opposite sides are also parallel. So the area of the square can be found by measuring the space occupied within the square. The formula to calculate the square of its side gives it.
If ‘a’ is the side of the square, then its area is given by ${a}^2$.

Area of a Square
Solved Word Problems on the Area of a Square
Some Solved Word Problems on the Area of a Square are given below:
Q 1. Find the area of a square whose length is 10 cm.
Ans: Given the length of a square = 10 cm

Square of 10 cm
Area of a square $=$ length $\times$ length
$=10 \times 10 \mathrm{~cm}^2$
$=100 \mathrm{~cm}^2$
Thus, the area of the square is $100 \mathrm{~cm}^2$
Q 2. Find the area of a square whose side measures 45 cm.
Ans: Given the length of a square = 45 cm

Square of 45 cm
Area of a square $=$ length $\times$ length
$=45 \times 45 \mathrm{~cm}^2$
$=2025 \mathrm{~cm}^2$
Thus, the area of the square is $2025 \mathrm{~cm}^2$.
Q 3. The length of a side of a square field is 200 m. What will be the cost of levelling the field at a rate of 10 rs per square metre?
Ans: Length of the square field = 200 m
Area of the field $=$ side $\times$ side
$=200 \mathrm{~m} \times 200 \mathrm{~m}$
$=40000 \mathrm{~m}^2$
Cost of levelling the field $=40000 \times 10 \mathrm{Rs}$
$=400000 \mathrm{Rs}$
Thus, the cost of levelling the field is 400000 Rs.
Practice Problems on the Area of a Square
Try the given practice problems on the area of a square:
Q 1. Find the area of the square whose sides are given below:
(i) 15 m
(ii) 250 m
(iii) 5 cm
(iv) 40 cm
(v) 10 m
Ans: (i) $225 \mathrm{~m}^2$
(ii) $62500 \mathrm{~m}^2$
(iii) $25 \mathrm{~cm}^2$
(iv) $1600 \mathrm{~cm}^2$
(v) $100 \mathrm{~m}^2$
Q 2. Find the area of the square of side $16 \mathrm{~cm}$.
Ans: $256 \mathrm{~cm}^2$
Q 3. Find the length of the square whose area is $100 \mathrm{~cm}^2$.
Ans: 10 cm
Summary
In this article, we learned about a quadrilateral square with four equal sides and all the angles as right angles, i.e. 90 degrees. The square's diagonals are equal and bisect each other at 90 degrees. We also learned about the various properties of squares and how we can calculate the area of squares. We also discussed the area of square examples to get to know how to find the area of a square of a given length easily.
FAQs on Area Word Problems Made Easy
1. What is the first step to solving an area word problem?
The first and most important step is to read the problem carefully to understand what is being asked. You need to identify the shape mentioned (e.g., a square field, a rectangular room) and the given measurements (like length, width, or side). Drawing a simple diagram of the shape is a helpful strategy to visualise the problem before applying any formula.
2. How do you find the area of a rectangle or a square in a word problem?
Once you have identified the shape and its dimensions from the word problem, you must use the correct formula.
- For a rectangle, the area is calculated by multiplying its length and width: Area = Length × Width.
- For a square, since all sides are equal, you find the area by multiplying the side by itself: Area = Side × Side.
3. How can you avoid confusing area and perimeter in word problems?
This is a common point of confusion. To avoid mistakes, remember the core difference in what they measure:
- Area measures the space inside a 2D shape. Look for keywords like "cover," "paint a surface," or "space occupied." Think of carpeting a room.
- Perimeter measures the distance around the boundary of a shape. Look for keywords like "fencing," "border," "frame," or "distance around." Think of putting a fence around a garden.
4. What are some real-world examples where we solve for area?
Area calculations are used in many everyday situations. Some common examples include:
- Calculating the amount of paint needed to cover a wall.
- Finding out how much carpet is required for a specific room.
- Determining the number of tiles needed to cover a floor space.
- Figuring out the total space of a garden plot to plan how many seeds to buy.
5. How do you solve a word problem if the area is given, but you need to find a missing side?
This type of problem requires you to work backwards using the area formula. First, write down the formula for the given shape. For a rectangle, this is Area = Length × Width. If you are given the area and the length, you can find the width by rearranging the formula to be Width = Area ÷ Length. Similarly, to find the side of a square when its area is known, you calculate the square root of the area (Side = √Area).
6. Why is it crucial to use square units (like m² or cm²) for the answer in an area problem?
Using square units is crucial because area is a two-dimensional measurement; it has both length and width. A simple unit like 'm' (metre) measures only length (one dimension). A 'square metre' (m²) represents an actual square measuring 1 metre by 1 metre. Therefore, the unit must show that you are measuring the total number of these small squares that can fit inside the larger shape, which is the fundamental definition of area.
7. If a word problem involves calculating cost, how does area help find the answer?
In multi-step problems, area is often the first part of the solution. For example, if you need to find the total cost of tiling a floor, you first calculate the total area of the floor in square metres. Then, if the cost is given per square metre, you multiply the total area by the cost per unit to find the total expense. The formula would be: Total Cost = Total Area × Cost per Square Unit.















