




Quick Formula, Tricks, and FAQs for Degrees to Radians
In Geometry, angles are measured using two different units: degrees and radians. The numerical numbers for travelling "one round" of a circle equals 360 degrees or 2π radians. The degree, denoted by the symbol (°), is the most extensively used and well-known unit for measuring angles. Another angle measurement unit in geometry is called a radian, in short Rad. When determining the angles of trigonometric or periodic functions, radians are usually taken into account.
In this article, we will study how to convert into radian measure as well as several solved problems to convert into radians using the conversion formula. So, let's start by discussing what degrees and radians are.
What is Degree Measure?
A full 360-degree rotation defines a unit of angular measurement known as a degree, denoted by the symbol °. One degree is equal to π/180 radians since a full revolution equals 2π radians. As an alternative to utilising the decimal form, degrees can alternatively be stated using minutes and seconds. Prime (′) and double-prime (′′) letters are used to denote minutes and seconds.
1° = 0.017453 radians
What is Radian Measure?
To comprehend the radian measure or radian (Rad), we must first talk about central angles, which are angles with their vertex in the centre of a circle. The length of the corresponding arc, which is equal to the radius, is used to calculate the radian of a central angle. In other words, when the radius is curved around the circumference of a circle, the angle measured by the resulting arc is called a radian. Look at the example below.
1 radian = 57.2958°.
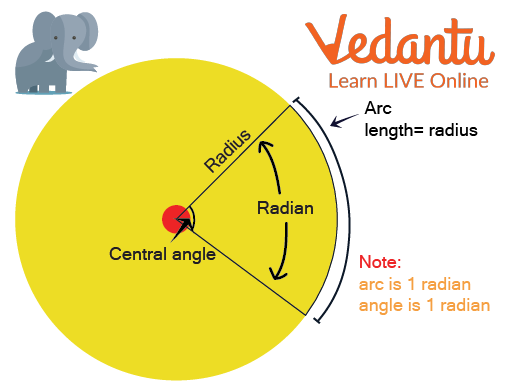
Radian Measure
Convert into Radian Formula
The formula for converting degrees to radians is a more general formula that may be used to change a given value in degrees to a value in radians and vice versa.
Radians = Degrees × π/180

Degrees to Radian Conversion Formula
How to Convert 60 Degrees into Radian?
The steps listed below demonstrate how to convert 60 degrees into radians:
Step 1: Write the number of degrees that you want to convert to radians, i.e 60.
Step 2: To convert from degrees to radians, multiply the number of degrees, i.e. 60 by π/180.
Step 3: Since your answer would be in radians, you can remove the degree sign.
Step 4: Simplify the expression obtained, i.e.
60 × π/180 = π/3.
Thus, the angle measurement in radians will be π/3 on simplification.
Note: The same procedure used to convert positive degrees into radians is applied to convert negative degrees. Simply multiply the angle's value given in degrees by π /180.
Solved Problems to Convert into Radian
Example 1: Convert into radian measure, 200 degrees.
Ans: We are aware of the formula.
Angle in radians = Angle in degree × π/180
Therefore, 200 degrees in radians are
= 200 × π/180
= 10π/9
= 3.491 Rad.
Example 2: In one minute, a wheel completes 360 revolutions. How many radians does it rotate around in a second?
Ans: It is given that the wheel does 360 total revolutions in a minute.
1 second = 360/60 = 6 revolutions
The fact that a wheel travels 2π radians in its single rotation. It will rotate a 360 x 2π radian =720π radian in a minute
Then in one second, it will turn an angle of
720π radian/60 = 12π radian
Therefore, the wheel makes a 12π radian turn in one second.
Practice Problems
1. Convert into radian measure: 700⁰
Ans. 12.21 Rad.
2. Determine the radians equivalent to 450 degrees.
Ans. 7.854 Rad.
3. Convert into radian measure, -300°.
Ans. -5.23 Rad.
Summary
We have discussed above, the two ways to measure the angle of a circle: in degrees and radians. We may convert between the two using formulae. Two rad or 360° are the same as one full circle. One radian (rad) equals 57.2958 degrees, and one degree is equal to 0.017453 radians (rad). An angle is multiplied by π/180⁰ to convert it from degrees to radians. This article has also covered how to convert 60° into radians. Try to solve the practice problems provided in this article using the degrees into radians conversion formula.
FAQs on Degrees to Radians Conversion Explained
1. What is the fundamental formula used to convert an angle from degrees to radians?
To convert an angle from degrees to radians, you multiply the given degree measure by the conversion factor (π / 180). The relationship is based on the fact that a full circle is 360°, which is equivalent to 2π radians. Therefore, the formula is: Radians = Degrees × (π / 180).
2. What does one 'radian' actually represent in relation to a circle?
One radian is defined as the angle created at the center of a circle by an arc whose length is equal to the radius of that circle. Unlike degrees, which are an arbitrary division of a circle, a radian is a natural unit of angular measure derived directly from the circle's own properties. This makes it a more fundamental unit in mathematics and physics.
3. Why are radians preferred over degrees in higher-level mathematics like calculus?
Radians are preferred in higher-level mathematics and physics because they simplify key formulas. For instance, the derivatives of trigonometric functions like sin(x) and cos(x) are straightforward only when x is in radians. Using degrees would introduce a constant factor of (π/180) into these calculations, making them much more complex. Radians are also essential for topics like angular velocity and simple harmonic motion.
4. How do you convert common angles like 30°, 45°, and 90° into radians in terms of π?
You use the standard conversion formula, Degrees × (π / 180), and simplify the fraction. It's best to leave the answer in terms of π for precision. Here are the conversions for common angles:
30°: 30 × (π/180) = π/6 radians
45°: 45 × (π/180) = π/4 radians
60°: 60 × (π/180) = π/3 radians
90°: 90 × (π/180) = π/2 radians
5. What is the significance of a negative angle, for example, -60°, when converting to radians?
The sign of an angle indicates its direction of rotation from the initial side. By convention, a positive angle is measured in the counter-clockwise direction, while a negative angle is measured in the clockwise direction. The conversion process is the same; a negative degree measure will simply result in a negative radian measure. For instance, -60° converts to -π/3 radians, representing a 60-degree rotation in the clockwise direction.
6. How do you handle an angle given in degrees, minutes, and seconds when converting to radians?
To convert an angle with minutes (') and seconds ("), you must first convert the entire measurement into a single decimal degree value. Follow these steps:
Convert seconds to minutes by dividing by 60.
Add this value to the original minutes.
Convert the total minutes to degrees by dividing by 60.
Add this decimal value to the original whole degrees.
Finally, multiply the total decimal degree value by (π / 180) to get the radian measure.
7. Why is it generally better to express radian measures as fractions of π instead of decimal approximations?
Expressing radian measures as fractions of π maintains mathematical precision and clarity. Since π is an irrational number, any decimal form is an approximation. Using a fraction like π/2 is an exact value. It also makes it easier to understand the angle's relationship to a full circle (2π) and to perform further trigonometric calculations without introducing rounding errors.















