




How to Calculate the Area of Shaded Regions in Maths
The area of the shaded region is basically the difference between the area of the complete figure and the area of the unshaded region. For finding the area of the figures, we generally use the basic formulas of the area of that particular figure. There is no specific formula to find the area of the shaded region of a figure as the amount of the shaded part may vary from question to question for the same geometric figure.
What is Area ?
Area is basically the amount of space occupied by a figure. The unit of area is generally square units; it may be square meters or square centimeters and so on.
Formula for Area of Geometric Figures :
Area of a square \[ = \] side \[ \times \] side
Area of a triangle \[ = \dfrac{1}{2} \times \] base \[ \times \] height
Area of a circle \[ = \] \[\pi {{\rm{r}}^2}\]
Area of a parallelogram \[ = \] base \[ \times \] height
Area of a trapezium \[ = \dfrac{1}{2}\] \[ \times \]sum of the length of the parallel sides \[ \times \] height
Area of rhombus \[ = \dfrac{1}{2}\] \[ \times \] product of the diagonals
What is the Area of the Shaded Region ?
In a given geometric figure if some part of the figure is coloured or shaded, then the area of that part of figure is said to be the area of the shaded region.
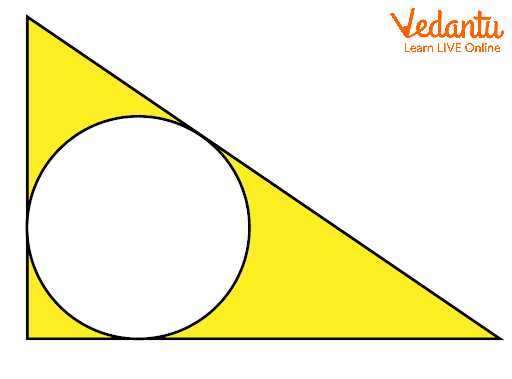
Example on how to Find Area of the Shaded Region
How to Find the Area of the Shaded Region?
So, the area of the shaded or coloured region in a figure is equal to the difference between the area of the entire figure and the area of the part that is not coloured or not shaded.
Area of the shaded region \[ = \] Area of the complete figure \[ - \] Area of the unshaded part
In the above image, if we are asked to find the area of the shaded region; we will calculate the area of the outer right angled triangle and then subtract the area of the circle from it. The remaining value which we get will be the area of the shaded region.
Solved Examples :
1. Find the area of the shaded region from the given figure :

Area of the Shaded Region
Solution :
Here, the length of the given rectangle is 48 cm and the breadth is 22 cm.
We can observe that the outer rectangle has a semicircle inside it. From the figure we can observe that the diameter of the semicircle and breadth of the rectangle are common.
So from this figure we can understand that the area of the shaded region for this figure will be equal to the difference between the area of the outer rectangle and the area of the inner semicircle.
We know that, Area of rectangle = length \[ \times \] breadth
∴ Area of the given rectangle = 48 cm \[ \times \] 22 cm \[ = 1056\] sq.cm
Also, Area of a semicircle = \[\dfrac{1}{2}\pi {r^2}\]
Here, diameter \[ = 22\] cm
So, Radius \[ = \dfrac{1}{2} \times \] Diameter \[ = \dfrac{1}{2} \times 22 = 11\]cm
Area of the given semicircle \[ = \dfrac{1}{2} \times \dfrac{{22}}{7} \times 11 \times 11 = \dfrac{{2662}}{{14}} = 190.14\]sq.cm
Therefore, Area of the shaded region = Area of rectangle - Area of semicircle
So, Area of the shaded region in the given figure = 1056 - 190.14 = 865.86 sq.cm
Area of the shaded region in the given figure is 865.86 sq.cm.
2. Find the area of the shaded region from the given figure :
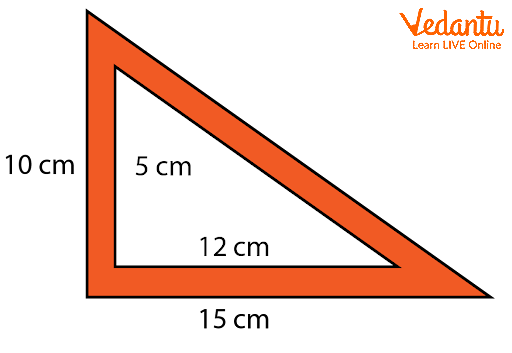
Area of the Shaded Region
Solution :
Here, the base of the outer right angled triangle is 15 cm and its height is 10 cm.
Similarly , the base of the inner right angled triangle is given to be 12 cm and its height is 5 cm.
We can observe that the outer right angled triangle has one more right angled triangle inside.
So from this figure we can understand that the area of the shaded region for this figure will be equal to the difference between the area of the outer triangle and the area of the inner triangle.
We know that, Area of a triangle \[ = \] \[\dfrac{1}{2}\] \[ \times \] base \[ \times \] height
∴ Area of the outer right
angled triangle \[ = \dfrac{1}{2} \times 15 \times 10 = \dfrac{1}{2} \times 150 = 75\] sq.cm.
Similarly, area of the inner
right angled triangle \[\dfrac{1}{2} \times 12 \times 5 = \dfrac{1}{2} \times 60 = 30\]sq.cm.
Therefore, Area of the shaded
region = Area of the outer triangle - Area of the inner triangle
We know that, Area of a triangle \[ = \dfrac{1}{2} \times {\rm{base}}\times{\rm{height}}\]
∴ Area of the outer right angled triangle \[ = \dfrac{1}{2} \times 15 \times 10 =\dfrac{1}{2}\times 150 = 75\] sq.cm.
Similarly,
area of the inner right angled triangle \[\dfrac{1}{2} \times 12 \times 5 = \dfrac{1}{2} \times 60 = 30\] sq.cm.
Therefore, Area of the shaded region \[ = \] Area of the outer triangle \[ - \] Area of the triangle. So, Area of the shaded region in the given figure \[ = 75 - 30 = 45\] sq.cm
Area of the shaded region in the given figure is 45 sq.cm.
3. Find the area of the shaded region from the given figure :
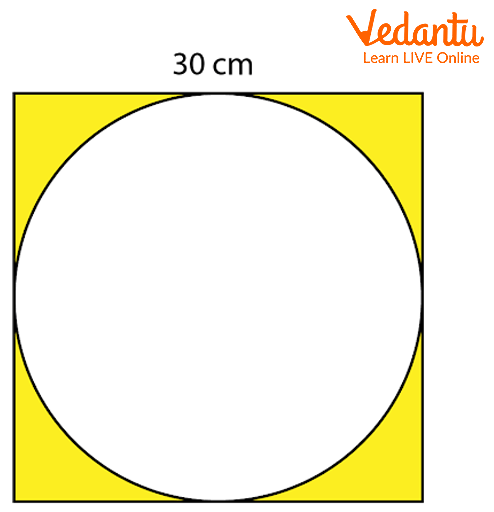
Area of the Shaded Region
Solution :
Here, the length of the side of the given square is 30 cm.
We can observe that the outer square has a circle inside it. From the figure we can see that the value of the side of the square is equal to the diameter of the given circle.
So from this figure we can understand that the area of the shaded region for this figure will be equal to the difference between the area of the outer square and the area of the inner circle. We know that, Area of square = side x side
∴ Area of the given square \[ = \] 30 cm \[ \times \] 30 cm \[ = \] 900 sq.cm
Also, Area of a circle \[ = \pi {r^2}\]
Here, diameter \[ = 30\] cm
So, Radius \[ = \dfrac{1}{2} \times \] Diameter \[ = \dfrac{1}{2} \times 30 = 15\]cm
Area of the given circle\[ = \dfrac{{22}}{7} \times 15 \times 15 = 49507 = 707.14\] sq.cm
\[ = \dfrac{{22}}{7} \times 15 \times 15 = \dfrac{{4950}}{7} = 707.14\] sq.cm
Therefore, Area of the shaded region = Area of square - Area of circle
So, Area of the shaded region in the given figure \[ = 900 - 707.14 = 192.86\] sq.cm
Area of the shaded region in the given figure is 192.86 sq.cm.
Conclusion
The area of the shaded region is in simple words the area of the coloured portion in the given figure. So, the ways to find and the calculations required to find the area of the shaded region depend upon the shaded region in the given figure.
FAQs on Area of Shaded Region Explained with Examples
1. What is the basic principle for finding the area of a shaded region?
The fundamental principle is to calculate the area of the larger, overall shape and then subtract the area of the unshaded portion(s) from it. The result is the area of the shaded region. In some cases, the shaded region might be a composite shape, requiring you to add the areas of its individual parts.
2. What is the general method to calculate the area of a shaded region?
To solve problems on the area of a shaded region, you can follow these general steps:
Step 1: Identify the larger shape and any smaller, unshaded shapes within it.
Step 2: Find the area of the larger, enclosing shape using its specific formula.
Step 3: Find the area of the unshaded shape(s) using their formulas.
Step 4: Subtract the total area of the unshaded parts from the area of the larger shape to get the final answer.
Always ensure your final answer is in square units (e.g., cm², m²).
3. How do you find the area of a shaded region that combines different geometric shapes, like a square and a circle?
When a figure combines shapes, you must break the problem down. For example, to find the area of a circle with an unshaded square inside it:
First, calculate the area of the circle using the formula A = πr².
Next, calculate the area of the square using the formula A = side².
Finally, subtract the area of the square from the area of the circle. The result, (Area of Circle) - (Area of Square), gives you the area of the shaded region.
4. What are some essential formulas you need to know for calculating shaded areas?
To solve most shaded area problems as per the CBSE/NCERT syllabus, you must be familiar with the area formulas for basic geometric shapes:
Square: Area = side × side
Rectangle: Area = length × width
Circle: Area = πr² (where 'r' is the radius)
Triangle: Area = ½ × base × height
Semicircle: Area = ½ × πr²
Quarter Circle: Area = ¼ × πr²
Triangle (Heron's Formula): Used when three sides (a, b, c) are known. Area = √[s(s-a)(s-b)(s-c)], where s is the semi-perimeter, s = (a+b+c)/2.
5. Is there a single, universal 'formula' for the area of a shaded region?
No, there is no single formula for the area of a shaded region. It is a concept that relies on a problem-solving strategy rather than a specific formula. The method changes based on the shapes involved and which part is shaded. The key is to see the shaded area as a combination (addition) or a remainder (subtraction) of simpler, known shapes.
6. Why is subtracting areas the most common strategy used for these problems?
Subtracting areas is the most common strategy because shaded regions in textbook problems are often designed as a well-defined larger shape with a piece 'cut out' from it. This 'cut-out' is also a standard geometric shape. Therefore, the shaded portion represents the area that is 'left over'. Describing this leftover area is mathematically simplest through subtraction: (Total Area) - (Area of Removed Part).
7. What is a common mistake students make when calculating the area of shaded regions?
A very common mistake is using the wrong dimensions, especially in problems involving circles. For instance, a student might use the diameter instead of the radius in the area formula (A = πr²), or miscalculate the side of a square inscribed in a circle. Another frequent error is incorrectly identifying which areas to add and which to subtract in a complex figure with multiple overlapping shapes.
8. How does finding the area of a shaded region apply in real-world scenarios?
This concept has many practical applications. For example:
In landscaping, you might calculate the area of a lawn that needs to be seeded, excluding a circular flowerbed in the middle.
In home improvement, you could find the area of a wall that needs to be painted, subtracting the areas of windows and doors.
In engineering and design, it's used to calculate the surface area of a machine part with holes or cutouts.















