




What are 2-Dimensional and 3-Dimensional Shapes?
Everything we observe in the world has a shape. In the objects we see around us, we can find different basic shapes such as the two-dimensional square, rectangle, and oval, as well as the three-dimensional rectangular prism, cylinder, and sphere. Credit cards, notes and coins, finger rings, photo frames, dart boards, houses, windows, magician's wands, high buildings, flower pots, toys, and balloons are all examples of geometric shapes.
The number of sides or corners of a shape changes from one to another. A side, or vertex, is a straight line that forms part of a shape, and a corner, or vertex, is the point where two sides meet. You're already familiar with the most common shapes, and may not be able to explain the differences between a square and a cube, or a circle and a sphere. In this article you'll start analysing and comparing 2D and 3D shapes, explaining their similarities, differences, and properties.
What are 2D shapes?
2D stands for two-dimensional in 2D shapes. Shapes with two dimensions, such as width and height, are known as 2D shapes. A rectangle or a circle are examples of 2D shapes because they don’t have depth. Basically 2D objects are flat and can't be physically held. We usually refer to dimensions as measurements in a specific direction. Length, width or breadth, depth, and height are examples of dimensions.
Examples of 2D Shapes:
Circle
There is just one bent side of a circle.
A semi-circle has two sides, one curved and one straight.
The full arc of the semi-circle measures 180 degrees.
Triangle
An equilateral triangle is a triangle with each angle measuring 60°.
Any triangle with one right angle is a right-angled triangle.
An irregular triangle is a scalene triangle. All of the sides and angles are unique.
Two sides and two angles of an isosceles triangle are the same.
Quadrilaterals
A square is a regular quadrilateral with 90o angles on all sides.
The diagonals of a kite intersect at right angles and have two sets of equal length sides.
A rectangle is made up of two sets of parallel straight lines, each with a 90° angle.
A rhombus has equal sides and opposite equal angles, as well as two sets of parallel lines.
One pair of parallel lines makes up a trapezium.
Two pairs of parallel lines with opposite equal angles make up a parallelogram.
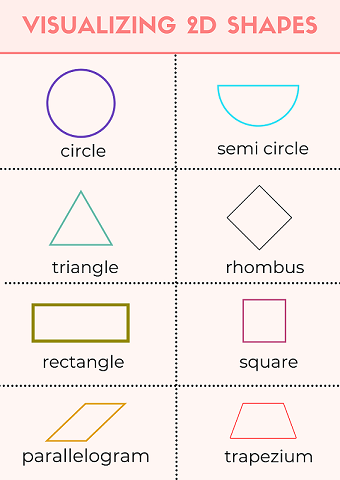
Image Shows the Illustration of 2D Shapes
3D Shapes
3D means it has three dimensions. So , it isn't flat like a 2D shape. The dimensions of 3D shapes include length, breadth, and depth. Examples of 3D shapes include spheres, cuboids, cubes, square-based pyramids, cylinders, and cones.
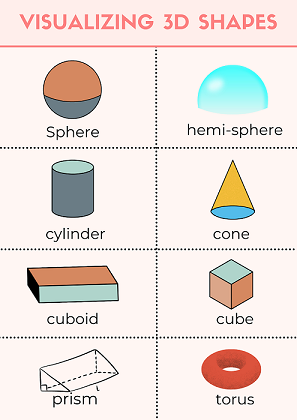
Image Shows the Illustration of 3D Shapes
Properties of 3D shapes
A 3D shape will have faces, edges and vertices.
A face on a 3D form is also known as a 'side.' It can be either flat or curved. As a result, a cube has six faces while a sphere has only one.
An edge is the point where two faces or sides of a face meet. You'll find 12 edges on a cube if you count the edges. However, a sphere, such as a ball, has no edges.
A corner is another name for a vertex. This is the point at where the edges meet.
Depending on the shape of the base, the properties of a pyramid can change. A square-based pyramid, for example, has five faces, while a triangle-based pyramid has four.
Differences Between 2D and 3D shapes
You might be confused by the differences between 2D and 3D shapes. There are some ways to measure an object in space. 3D objects can be measured in length, width, and height. 3D shapes, unlike 2D shapes, do not have a flat surface. Means they have depth. Two-dimensional shapes have two dimensions, while three-dimensional shapes have three dimensions. The most important thing for you to understand is that the primary difference between 2D and 3D shapes is their dimension.
Conclusion
2D and 3D shapes are maths topics that fall under geometry. They're covered in other portions of the curriculum as well. In year 3 shapes, you will study, analyse, and compare the qualities of 2D shapes, as well as create patterns using them and solve problems with them. Know how to spot 2D shapes in things like buildings, road signs, and other common objects. This article also gives you an introduction about 3D shapes which will help you in the higher classes.
FAQs on 2D and 3D Shapes: Types, Examples and Differences
1. What are 2D shapes? Provide some common examples.
A 2D shape is a flat figure that has only two dimensions: length and width. These shapes do not have any thickness or depth and can be drawn on a plane surface. Common examples of 2D shapes include:
- Square: A shape with four equal sides and four right angles.
- Circle: A round shape with all points on its boundary equidistant from the centre.
- Triangle: A three-sided polygon.
- Rectangle: A four-sided shape with opposite sides of equal length and four right angles.
2. What are 3D shapes and what are their key properties?
A 3D shape is a solid object that has three dimensions: length, width, and height (or depth). Unlike 2D shapes, they occupy space. The key properties of 3D shapes are defined by their faces, edges, and vertices.
- Faces: The flat or curved surfaces that make up the outside of a 3D shape.
- Edges: The lines where two faces meet.
- Vertices: The points or corners where the edges meet.
Examples include a cube, sphere, cone, and cylinder.
3. What is the main difference between 2D and 3D shapes?
The main difference between 2D and 3D shapes lies in the number of dimensions they have. A 2D shape is flat and has only two dimensions (length and width), so you can measure its area. In contrast, a 3D shape has three dimensions (length, width, and height), which means it has volume and occupies space. You can hold a 3D object, but a 2D shape can only be drawn on a flat surface.
4. Can you give some examples of 2D and 3D shapes found in real life?
Yes, shapes are all around us.
- Real-life 2D shape examples: A photograph (rectangle), a clock face (circle), a single tile on the floor (square), and a slice of pizza (triangle).
- Real-life 3D shape examples: A Rubik's Cube (cube), a football (sphere), an ice cream cone (cone), and a battery cell (cylinder).
5. How are the properties of a cube and a cuboid different from each other?
While both a cube and a cuboid have the same number of faces (6), edges (12), and vertices (8), the key difference lies in their faces. In a cube, all six faces are identical squares. In a cuboid, the faces are rectangles, and only the opposite faces are identical. A cube is a special type of cuboid where all edges are of equal length.
6. Why do some 3D shapes like spheres have curved surfaces instead of flat faces?
The structure of a 3D shape determines its surfaces. Shapes like cubes and pyramids, known as polyhedrons, are made up of flat polygonal surfaces called faces. However, some 3D shapes are not polyhedrons. A sphere, for example, is defined as a set of all points in three-dimensional space that are equidistant from a central point. This definition naturally creates a single, continuous curved surface with no edges or vertices. Similarly, a cylinder has two flat circular faces and one curved surface.
7. How can you describe a 3D shape by its faces, edges, and vertices?
To describe a 3D shape using its properties, you identify and count its three main components. Let's use a pyramid with a square base as an example:
- Faces: Count all the flat surfaces. A square base pyramid has 1 square face at the bottom and 4 triangular faces on the sides, making a total of 5 faces.
- Edges: Count all the lines where the faces meet. It has 4 edges on the base and 4 edges rising to the top point, making a total of 8 edges.
- Vertices: Count all the corners where edges meet. It has 4 vertices on the base and 1 vertex at the top (the apex), for a total of 5 vertices.
8. Why is understanding the difference between 2D and 3D shapes important outside of Maths?
Understanding 2D and 3D shapes is a fundamental skill that applies to many fields. In art and design, it is crucial for creating perspective in drawings and for product design. In architecture and engineering, it's the basis for creating blueprints and constructing buildings. In science, molecules are often represented as 3D structures. For everyone, it enhances spatial reasoning, which helps in everyday tasks like packing a box, reading a map, or arranging furniture.















