Answer
114.6k+ views
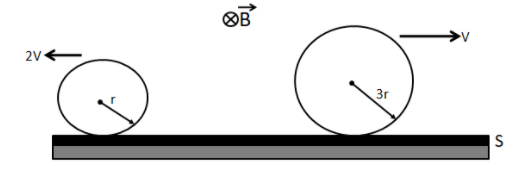
Hint: Note the direction of current for each of the loops and then find the highest and lowest potential points for each of the rings. Find the potential difference between the highest and lowest points for each of the rings from the given magnetic field and radius. The potential of the point on the surface is equal for both of the rings since they are in the same plane.
Find the potential difference between the highest points of the rings from each potential difference of these two rings.
Formula used:
If $A$ is the highest potential point and \[E\] is the lowest potential point of the ring of radius \[r\] moving with a speed $2v$,
The potential difference between two points, ${V_{AE}} = B(2r)(2v)$
and, if $C$ is the highest potential point and $D$ is the lowest potential point, of the ring of radius $3r$ moving with a speed $v$,
The potential difference between two points, ${V_{CD}} = B(2 \times 3r)(v)$
Where, $B$ is the magnetic field acting perpendicular to the plane of the rings.
The potential difference, $V = {V_{CD}} - ( - {V_{AE}}) = {V_{CD}} + {V_{AE}}$
Complete step by step solution:
For the first ring, the direction of velocity is towards the left side. So if we apply Fleming’s right hand rule, the current is flowing from point $A$ to \[E\]. Hence, $A$ is the highest potential point and \[E\] is the lowest potential point of the ring.
Given, \[r\]is the radius of the ring and it is moving with a speed $2v$
$B$ is the magnetic field acting perpendicular to the plane of the rings.
$\therefore $ The potential difference between two points, ${V_{AE}} = B(2r)(2v)$
$ \Rightarrow {V_{AE}} = 4Brv$
For the second ring, the direction of velocity is towards the right side. So if we apply Fleming’s right-hand rule, the current is flowing from point $C$ to \[D\]. Hence, $C$ is the highest potential point and $D$ is the lowest potential point Given, \[3r\] is the radius of the ring and it is moving with a speed $v$
$\therefore $ The potential difference between two points, ${V_{CD}} = B(2 \times 3r)(v)$
$ \Rightarrow {V_{CD}} = 6Brv$
The potential difference ,$V = {V_{CD}} - ( - {V_{AE}}) = {V_{CD}} + {V_{AE}}$
$\therefore V = 6Brv + 4Brv = 10Brv$ .
Hence, the right answer is in option \[{\text{D}}{\text{. }}10{\text{ Brv}}\].
Note: The formula used for calculating the potential difference is coming from the equation of induced current in a straight conductor in motion, where the induced current $I = \dfrac{{Blv}}{R}$, $B$ is the magnetic field, $v$ is the motion, $l$ is the length of the straight conductor and $R$ is the resistance.
$ \Rightarrow IR = Blv$
$ \Rightarrow e = Blv$
$e$ is the electromotive force of the circuit, $e = IR$ [Ohm’s law]
In the above problem, the length of the straight conductor $l = 2r$ i.e the length is equal to the diameter of the ring.
Find the potential difference between the highest points of the rings from each potential difference of these two rings.
Formula used:
If $A$ is the highest potential point and \[E\] is the lowest potential point of the ring of radius \[r\] moving with a speed $2v$,
The potential difference between two points, ${V_{AE}} = B(2r)(2v)$
and, if $C$ is the highest potential point and $D$ is the lowest potential point, of the ring of radius $3r$ moving with a speed $v$,
The potential difference between two points, ${V_{CD}} = B(2 \times 3r)(v)$
Where, $B$ is the magnetic field acting perpendicular to the plane of the rings.
The potential difference, $V = {V_{CD}} - ( - {V_{AE}}) = {V_{CD}} + {V_{AE}}$
Complete step by step solution:
For the first ring, the direction of velocity is towards the left side. So if we apply Fleming’s right hand rule, the current is flowing from point $A$ to \[E\]. Hence, $A$ is the highest potential point and \[E\] is the lowest potential point of the ring.
Given, \[r\]is the radius of the ring and it is moving with a speed $2v$
$B$ is the magnetic field acting perpendicular to the plane of the rings.
$\therefore $ The potential difference between two points, ${V_{AE}} = B(2r)(2v)$
$ \Rightarrow {V_{AE}} = 4Brv$
For the second ring, the direction of velocity is towards the right side. So if we apply Fleming’s right-hand rule, the current is flowing from point $C$ to \[D\]. Hence, $C$ is the highest potential point and $D$ is the lowest potential point Given, \[3r\] is the radius of the ring and it is moving with a speed $v$
$\therefore $ The potential difference between two points, ${V_{CD}} = B(2 \times 3r)(v)$
$ \Rightarrow {V_{CD}} = 6Brv$
The potential difference ,$V = {V_{CD}} - ( - {V_{AE}}) = {V_{CD}} + {V_{AE}}$
$\therefore V = 6Brv + 4Brv = 10Brv$ .
Hence, the right answer is in option \[{\text{D}}{\text{. }}10{\text{ Brv}}\].
Note: The formula used for calculating the potential difference is coming from the equation of induced current in a straight conductor in motion, where the induced current $I = \dfrac{{Blv}}{R}$, $B$ is the magnetic field, $v$ is the motion, $l$ is the length of the straight conductor and $R$ is the resistance.
$ \Rightarrow IR = Blv$
$ \Rightarrow e = Blv$
$e$ is the electromotive force of the circuit, $e = IR$ [Ohm’s law]
In the above problem, the length of the straight conductor $l = 2r$ i.e the length is equal to the diameter of the ring.
Recently Updated Pages
JEE Main 2021 July 25 Shift 2 Question Paper with Answer Key

JEE Main 2021 July 25 Shift 1 Question Paper with Answer Key

JEE Main 2021 July 22 Shift 2 Question Paper with Answer Key

JEE Main 2021 July 20 Shift 2 Question Paper with Answer Key

Hybridization of Atomic Orbitals Important Concepts and Tips for JEE

Atomic Structure: Complete Explanation for JEE Main 2025

Trending doubts
JEE Main Login 2045: Step-by-Step Instructions and Details

JEE Main Exam Marking Scheme: Detailed Breakdown of Marks and Negative Marking

Collision - Important Concepts and Tips for JEE

Ideal and Non-Ideal Solutions Raoult's Law - JEE

Current Loop as Magnetic Dipole and Its Derivation for JEE

Two plane mirrors are inclined at angle theta as shown class 12 physics JEE_Main