
The resultant of $\vec A$ and $\vec B$ is perpendicular to $\vec A$. What is the angle between $\vec A$ and $\vec B$?
A) ${\cos ^{ - 1}}\left( {\dfrac{A}{B}} \right)$
B) ${\cos ^{ - 1}}\left( { - \dfrac{A}{B}} \right)$
C) ${\sin ^{ - 1}}\left( {\dfrac{A}{B}} \right)$
D) ${\sin ^{ - 1}}\left( { - \dfrac{A}{B}} \right)$
Answer
167.1k+ views
Hint: The resultant of two vectors is the vector addition of two vectors. Vectors can be added following two rules of addition: triangle law of addition or parallelogram law of addition. We can draw the vectors with co-initial points to illustrate the parallelogram law of vectors.
Formulae used:
The formula for the angle between resultant vector $\left( {\vec A + \vec B} \right)$ and a vector $\vec A$ is
$\tan \alpha = \dfrac{{b\sin \theta }}{{a + b\cos \theta }}$
Where $\alpha $ is the angle between resultant and the original vector and $\theta $ is the angle between the two vectors.
Complete step by step solution:
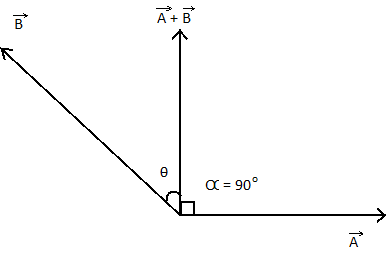
In the question it is given that the angle between resultant vector $\left( {\vec A + \vec B} \right)$ and a vector $\vec A$ is ${90^\circ }$ , that is, the resultant vector is perpendicular to the original vector.
$ \Rightarrow \alpha = {90^\circ }$
This means that
$\tan {90^\circ } = \dfrac{{B\sin \theta }}{{A + B\cos \theta }}$
As $\tan {90^\circ } \approx \infty $, for a fraction to approach infinity, the denominator of the fraction has to be zero
$A + B\cos \theta = 0$
$ \Rightarrow \cos \theta = - \dfrac{B}{A}$
$ \Rightarrow \cos \theta = - \dfrac{B}{A}$
$ \Rightarrow \theta = {\cos ^{ - 1}}( - \dfrac{B}{A})$
So the angle between the vectors is (B), ${\cos ^{ - 1}}\left( { - \dfrac{A}{B}} \right)$.
Additional information:
To derive the formula for the angle between the vectors we use the parallelogram law of vector addition. If $\vec A$ and $\vec B$ are vectors acting simultaneously from a point, representing both the magnitude and direction of the vectors, and $\theta $ is the angle between them then, then the diagonal of the parallelogram passing through the common vertices is the resultant. The angle between resultant and base is found by extending the base until a right angled triangle is formed and using Pythagoras and basic trigonometry to find the formula
Note: To solve such questions, we can also look at it from the point of view of triangle addition of vectors but that would make the formula more complicated. In parallelogram law of additions, both vectors and resultant share a common origin point, hence making the angle between the vectors more evident.
Formulae used:
The formula for the angle between resultant vector $\left( {\vec A + \vec B} \right)$ and a vector $\vec A$ is
$\tan \alpha = \dfrac{{b\sin \theta }}{{a + b\cos \theta }}$
Where $\alpha $ is the angle between resultant and the original vector and $\theta $ is the angle between the two vectors.
Complete step by step solution:

In the question it is given that the angle between resultant vector $\left( {\vec A + \vec B} \right)$ and a vector $\vec A$ is ${90^\circ }$ , that is, the resultant vector is perpendicular to the original vector.
$ \Rightarrow \alpha = {90^\circ }$
This means that
$\tan {90^\circ } = \dfrac{{B\sin \theta }}{{A + B\cos \theta }}$
As $\tan {90^\circ } \approx \infty $, for a fraction to approach infinity, the denominator of the fraction has to be zero
$A + B\cos \theta = 0$
$ \Rightarrow \cos \theta = - \dfrac{B}{A}$
$ \Rightarrow \cos \theta = - \dfrac{B}{A}$
$ \Rightarrow \theta = {\cos ^{ - 1}}( - \dfrac{B}{A})$
So the angle between the vectors is (B), ${\cos ^{ - 1}}\left( { - \dfrac{A}{B}} \right)$.
Additional information:
To derive the formula for the angle between the vectors we use the parallelogram law of vector addition. If $\vec A$ and $\vec B$ are vectors acting simultaneously from a point, representing both the magnitude and direction of the vectors, and $\theta $ is the angle between them then, then the diagonal of the parallelogram passing through the common vertices is the resultant. The angle between resultant and base is found by extending the base until a right angled triangle is formed and using Pythagoras and basic trigonometry to find the formula
Note: To solve such questions, we can also look at it from the point of view of triangle addition of vectors but that would make the formula more complicated. In parallelogram law of additions, both vectors and resultant share a common origin point, hence making the angle between the vectors more evident.
Recently Updated Pages
Classification of Elements and Periodicity in Properties | Trends, Notes & FAQs

Difference Between Orbit and Orbital in Chemistry Explained (With Table & Diagram)

Difference Between Intensive and Extensive Properties in Chemistry

Difference Between Evaporation and Boiling: Key Concepts, Table & Examples

Difference Between CNG and LPG: Explained with Table, Properties & Uses

Difference Between Cell and Battery – Key Differences, Diagram, and Examples

Trending doubts
JEE Main 2025 Session 2: Application Form (Out), Exam Dates (Released), Eligibility, & More

Uniform Acceleration

Displacement-Time Graph and Velocity-Time Graph for JEE

JEE Main 2025: Derivation of Equation of Trajectory in Physics

Atomic Structure - Electrons, Protons, Neutrons and Atomic Models

Learn About Angle Of Deviation In Prism: JEE Main Physics 2025

Other Pages
NCERT Solutions for Class 11 Physics Chapter 1 Units and Measurements

JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

NCERT Solutions for Class 11 Physics Chapter 2 Motion In A Straight Line

Units and Measurements Class 11 Notes: CBSE Physics Chapter 1

Motion in a Straight Line Class 11 Notes: CBSE Physics Chapter 2

Important Questions for CBSE Class 11 Physics Chapter 1 - Units and Measurement




