
The potential of $A$ is $10\;V$, then the potential of $B$ is:

(A) $\dfrac{{25}}{3}\;V$
(B) $\dfrac{{50}}{3}\;V$
(C) $\dfrac{{100}}{3}\;V$
(D) $50\;V$
Answer
173.4k+ views
Hint: Here we have a circuit with three capacitors having capacitance $1\mu F$ each. The potential at a particular point is given and we have to find the potential at another point. For that, we have to find whether the capacitors are in series or parallel combination and using equivalent circuits we have to find the potential.
Complete Step by step solution:
Here we have three capacitors of $1\mu F$ each. Let us consider the equivalent circuit as shown below
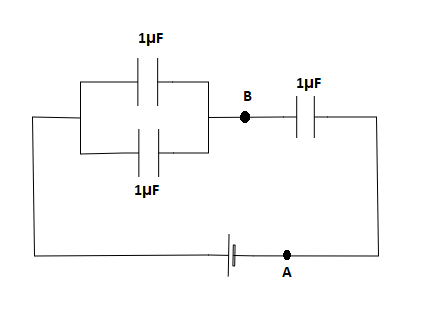
We can see that two of the capacitors are connected in parallel and we can write the equivalent capacitance of these two capacitors as,
${C_1} = 1\mu F + 1\mu F = 2\mu F$
The third capacitor is in series connection with the two capacitors that are in parallel. Now the equivalent circuit is as shown below,
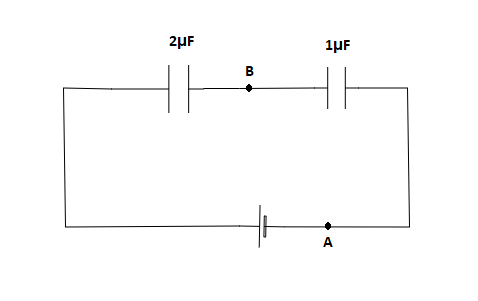
The potential across a capacitor is given by,
$V = \dfrac{Q}{C}$
where $Q$ stands for the charge stored in the capacitor and $C$ stands for the capacitance of the capacitor.
From this, we can write,
$Q = VC$
In a series combination, each capacitor carries the same amount of charge.
Since the two capacitors are in series connection the total capacitance can be written as,
$\dfrac{1}{C} = \dfrac{1}{{{C_1}}} + \dfrac{1}{{{C_2}}}$
The capacitance ${C_1} = 2\mu F$ and ${C_2} = 1\mu F$
Putting these values in the above equation, we get
$\dfrac{1}{C} = \dfrac{1}{2} + \dfrac{1}{1} = \dfrac{3}{2}$
The capacitance, $C = \dfrac{2}{3}$
The potential at $A$, $V = 10V$
Now the charge can be written as,
$Q = \dfrac{2}{3} \times 10 = \dfrac{{20}}{3}\mu C$
The voltage across the $1\mu F$ capacitor can be written as,
${V_B} - {V_A} = \dfrac{{20}}{3}$
where ${V_B}$ is the potential at the point $B$ and ${V_A}$ is the potential at the point $A$.
Substituting ${V_A} = 10V$ in the above equation we get
${V_B} = \dfrac{{20}}{3} + 10 = \dfrac{{50}}{3}V$
The answer is Option (B): $\dfrac{{50}}{3}V$
Note: A series combination is employed to decrease the effective capacitance. The effective capacitance will be lower than the lowest capacitance in the combination. The parallel combination is employed to increase the effective capacitance. The effective capacitance is higher than the highest value of capacitance in the combination.
Complete Step by step solution:
Here we have three capacitors of $1\mu F$ each. Let us consider the equivalent circuit as shown below

We can see that two of the capacitors are connected in parallel and we can write the equivalent capacitance of these two capacitors as,
${C_1} = 1\mu F + 1\mu F = 2\mu F$
The third capacitor is in series connection with the two capacitors that are in parallel. Now the equivalent circuit is as shown below,

The potential across a capacitor is given by,
$V = \dfrac{Q}{C}$
where $Q$ stands for the charge stored in the capacitor and $C$ stands for the capacitance of the capacitor.
From this, we can write,
$Q = VC$
In a series combination, each capacitor carries the same amount of charge.
Since the two capacitors are in series connection the total capacitance can be written as,
$\dfrac{1}{C} = \dfrac{1}{{{C_1}}} + \dfrac{1}{{{C_2}}}$
The capacitance ${C_1} = 2\mu F$ and ${C_2} = 1\mu F$
Putting these values in the above equation, we get
$\dfrac{1}{C} = \dfrac{1}{2} + \dfrac{1}{1} = \dfrac{3}{2}$
The capacitance, $C = \dfrac{2}{3}$
The potential at $A$, $V = 10V$
Now the charge can be written as,
$Q = \dfrac{2}{3} \times 10 = \dfrac{{20}}{3}\mu C$
The voltage across the $1\mu F$ capacitor can be written as,
${V_B} - {V_A} = \dfrac{{20}}{3}$
where ${V_B}$ is the potential at the point $B$ and ${V_A}$ is the potential at the point $A$.
Substituting ${V_A} = 10V$ in the above equation we get
${V_B} = \dfrac{{20}}{3} + 10 = \dfrac{{50}}{3}V$
The answer is Option (B): $\dfrac{{50}}{3}V$
Note: A series combination is employed to decrease the effective capacitance. The effective capacitance will be lower than the lowest capacitance in the combination. The parallel combination is employed to increase the effective capacitance. The effective capacitance is higher than the highest value of capacitance in the combination.
Recently Updated Pages
JEE Main Mock Test 2025-26: Free Practice & Solutions

JEE Main Mock Test 2025-26: Free Online Practice Series

JEE Main 2025-26 Mock Tests: Free Practice Papers & Solutions

JEE Main 2025 Dual Nature of Matter Mock Test – Free Practice PDF

Kinetic Theory Of Gases Mock Test 2025

Optics Mock Test 2025: Free Practice Questions & Answers

Trending doubts
JEE Main 2025 Session 2: Application Form (Out), Exam Dates (Released), Eligibility, & More

Displacement-Time Graph and Velocity-Time Graph for JEE

Uniform Acceleration

Electric field due to uniformly charged sphere class 12 physics JEE_Main

JEE Main 2025: Derivation of Equation of Trajectory in Physics

Atomic Structure - Electrons, Protons, Neutrons and Atomic Models

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

Learn About Angle Of Deviation In Prism: JEE Main Physics 2025

Enthalpy of Combustion with Examples for JEE

Instantaneous Velocity - Formula based Examples for JEE

JEE Advanced Weightage 2025 Chapter-Wise for Physics, Maths and Chemistry

Essential Derivations for CBSE Class 12 Physics: Stepwise & PDF Solutions




