
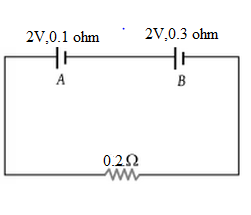
The internal resistance of two cells shown are \[0.1\Omega \] and \[0.3\Omega \]. If \[R = 0.2\Omega \], the potential difference across the cell:
A) B will be zero
B) A will be zero
C) A and B be \[2V\]
D) A will be \[ > 2V\] and B will be \[ < 2V\].
Answer
173.1k+ views
Hint: According, Kirchhoff’s voltage law (KVL), the algebraic sum of voltages across each element is zero. Kirchhoff’s voltage law is used to calculate the value of potential difference across the cell. From KVL, We get the value of current flowing through the circuit. Then we calculate potential difference across B by substituting the value of current in the KVL equation.
Formula used:
We apply Kirchhoff’s voltage law (KVL) in circuit. Then we calculate potential differences across B.
Complete step by step solution:
Given: Resistances are \[0.1\Omega \], \[0.3\Omega \] and \[0.2\Omega \]. Voltages are \[2V\] each.
Let us suppose that the current flowing through the circuit is I.
On applying: Kirchhoff’s voltage law (KVL) in given circuit , we get following equation
\[ - (0.2)I - (0.3)I + 2V - (0.1)I + 2V = 0\]
\[ \Rightarrow 0.6I = 4\]
\[ \Rightarrow I = \dfrac{4}{{0.6}} = \dfrac{{40}}{6}A\]
\[\therefore I = \dfrac{{20}}{3}A\]
Hence, current flows through the circuit, \[I = \dfrac{{20}}{3}A\]
Now, potential difference across B is calculated by
\[{V_1} - (0.3)\dfrac{{20}}{3} + 2V = {V_2}\]
\[ \Rightarrow {V_1} - 2V + 2V = {V_2}\]
\[ \Rightarrow {V_1} = {V_2}\]
\[\therefore\] Potential difference across \[B = {V_1} - {V_2} = 0\]
Hence, Potential difference across B is zero.
Therefore, the correct option is (D).
Additional information: Kirchhoff’s voltage law (KVL) is also known as the second rule of Kirchhoff’s. According to this rule, the algebraic sum of voltages in a closed circuit is zero. Kirchhoff’s voltage law is applicable for both AC and DC circuits. Voltage across passive elements in a closed circuit is always equivalent. The value of voltage is reverse to source voltage.
To measure the unknown standards such as current (I), Voltage (V) we use, Kirchhoff's laws are used, KVL is also used to find the direction of moving current in the circuit. This rule is very useful to solve complicated circuitries. To observe the transferal of power in the circuit, we use KVL in circuits.
Note: Students be careful to apply Kirchhoff’s voltage law (KVL) in circuit. Direction of current is mandatory to apply Kirchhoff’s voltage law.
Formula used:
We apply Kirchhoff’s voltage law (KVL) in circuit. Then we calculate potential differences across B.
Complete step by step solution:
Given: Resistances are \[0.1\Omega \], \[0.3\Omega \] and \[0.2\Omega \]. Voltages are \[2V\] each.
Let us suppose that the current flowing through the circuit is I.
On applying: Kirchhoff’s voltage law (KVL) in given circuit , we get following equation
\[ - (0.2)I - (0.3)I + 2V - (0.1)I + 2V = 0\]
\[ \Rightarrow 0.6I = 4\]
\[ \Rightarrow I = \dfrac{4}{{0.6}} = \dfrac{{40}}{6}A\]
\[\therefore I = \dfrac{{20}}{3}A\]
Hence, current flows through the circuit, \[I = \dfrac{{20}}{3}A\]
Now, potential difference across B is calculated by
\[{V_1} - (0.3)\dfrac{{20}}{3} + 2V = {V_2}\]
\[ \Rightarrow {V_1} - 2V + 2V = {V_2}\]
\[ \Rightarrow {V_1} = {V_2}\]
\[\therefore\] Potential difference across \[B = {V_1} - {V_2} = 0\]
Hence, Potential difference across B is zero.
Therefore, the correct option is (D).
Additional information: Kirchhoff’s voltage law (KVL) is also known as the second rule of Kirchhoff’s. According to this rule, the algebraic sum of voltages in a closed circuit is zero. Kirchhoff’s voltage law is applicable for both AC and DC circuits. Voltage across passive elements in a closed circuit is always equivalent. The value of voltage is reverse to source voltage.
To measure the unknown standards such as current (I), Voltage (V) we use, Kirchhoff's laws are used, KVL is also used to find the direction of moving current in the circuit. This rule is very useful to solve complicated circuitries. To observe the transferal of power in the circuit, we use KVL in circuits.
Note: Students be careful to apply Kirchhoff’s voltage law (KVL) in circuit. Direction of current is mandatory to apply Kirchhoff’s voltage law.
Recently Updated Pages
JEE Main Mock Test 2025-26: Thermodynamics Practice & Tips

JEE Main 2025-26 Mock Test: Properties of Solids and Liquids

JEE Main Gravitation Mock Test 2025-26 – Free Practice Online

JEE Main Rotational Motion Mock Test 2025-26: Free Practice Online

JEE Main 2025-26 Work, Energy and Power Mock Test – Free Practice Online

JEE Main Mock Test 2025-26: Laws of Motion Practice Online

Trending doubts
JEE Main 2025 Session 2: Application Form (Out), Exam Dates (Released), Eligibility, & More

Displacement-Time Graph and Velocity-Time Graph for JEE

Uniform Acceleration

Electric field due to uniformly charged sphere class 12 physics JEE_Main

JEE Main 2025: Derivation of Equation of Trajectory in Physics

Atomic Structure - Electrons, Protons, Neutrons and Atomic Models

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

Learn About Angle Of Deviation In Prism: JEE Main Physics 2025

Enthalpy of Combustion with Examples for JEE

Instantaneous Velocity - Formula based Examples for JEE

JEE Advanced Weightage 2025 Chapter-Wise for Physics, Maths and Chemistry

Essential Derivations for CBSE Class 12 Physics: Stepwise & PDF Solutions




