Question

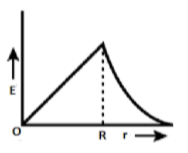
The electric field due to a uniformly charged sphere of radius $R$ as a function of the distance from its centre is represented graphically by:
A)

B)

C)

D)

Answer 1

Hint: A graph between electric fields due to a uniformly charged sphere and the distance from the centre of charge sphere is needed to be plotted. It should be kept in mind that the electric field inside the charged sphere is different and the electric field outside the charged sphere is different. The relationship between distance and electric field would also be different inside the charged sphere and outside the charged sphere.

Complete step by step solution:
Let the distance from the centre of the sphere be represented by $r$ .
Now, Case 1: $(r \leqslant R)$ When distance $r$ is less than the radius of the charged sphere that is $R$ .
As we know that, inside a charged sphere of charge $Q$ at distance $r$ from centre is given by,
 $E = \dfrac{{Qr}}{{4\pi {\varepsilon _o}{R^3}}}$
 As we have to plot Electric field as a function of distance from the centre so in the above relation we can see that, Electric field is directly proportional to the distance from the centre. This can be expressed in the form of an expression as,
$E \propto r$
So, when $(r \leqslant R)$ the Electric field would be directly proportional to distance from the centre.
 Now, Case 2: $(r \geqslant R)$
When distance $r$ is more than the radius of the charged sphere that is $R$ .
As we know that, outside a charged sphere of charge $Q$ at distance $r$ from centre is given by,
$E = \dfrac{Q}{{4\pi {\varepsilon _o}{r^2}}}$
 As we have to plot Electric field as a function of distance from the centre so in the above relation we can see that, Electric field is inversely proportional to the square of the distance from the centre. This can be expressed in the form of an expression as,
$E \propto \dfrac{1}{{{r^2}}}$
So, when $(r \leqslant R)$ the Electric field would be inversely proportional to the square of the distance from the centre.

Hence option B is the correct answer.

Note: Here it is important to note why the electric field is different inside and outside of the charged sphere. The electric field outside the sphere is seen to be identical to that of a point charge $Q$ at the centre of the sphere. For a radius $(r < R)$ , a Gaussian surface will enclose less than the total charge and the electric field will be less.