
Answer
114.3k+ views
Hint: To find the radius of the largest circle which passes through the focus of the parabola and is contained in the parabola, we will find the centre of the parabola by making the general equation of circle pass through the focus of the parabola and solve it in terms of radius of the circle.
Complete step by step answer:
We have the equation of parabola as ${{y}^{2}}=4x $.
We want to find the radius of the largest circle which passes through the focus of the parabola.
We know the focus of the parabola of the form \[{{y}^{2}}=4ax\] is \[(a,0)\] .
Thus, the focus of the parabola \[{{y}^{2}}=4x\] is \[(1,0)\] .
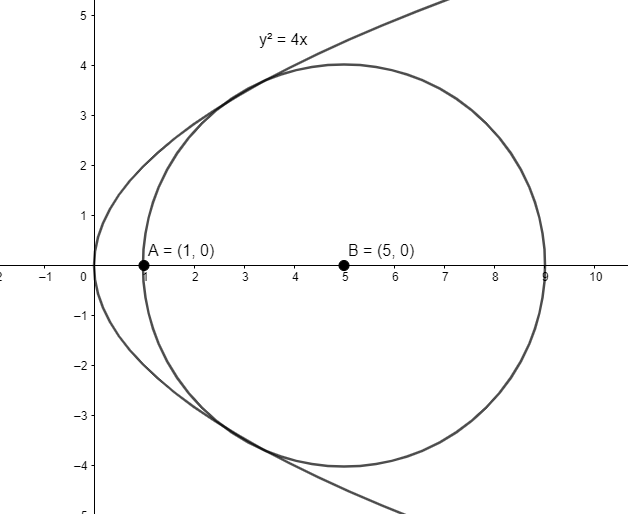
As we want the largest circle contained in parabola \[{{y}^{2}}=4x\] and the circle passes through focus of parabola, the centre of the circle lies on \[x\] -axis.
Let’s assume that the centre of the circle is \[(h,0)\] .
Let the radius of the circle be \[r\] .
As the circle passes through \[(1,0)\] , we have \[h=1+r\] . \[(1)\]
We know the equation of circle passing through the point \[(h,k)\] is of the form \[{{(x-h)}^{2}}+{{(y-k)}^{2}}={{r}^{2}}\] .
So, the equation of our circle is \[{{(x-h)}^{2}}+{{y}^{2}}={{r}^{2}}\]
Substituting the value of \[h\] from equation \[(1)\] , we get \[{{(x-1-r)}^{2}}+{{y}^{2}}={{r}^{2}}\] .
\[\Rightarrow {{x}^{2}}+{{r}^{2}}+1-2x-2xr+2r+{{y}^{2}}={{r}^{2}}\]
\[\Rightarrow {{x}^{2}}+{{y}^{2}}-2x-2xr+1+2r=0\]
But, we know \[{{y}^{2}}=4x\] . Substituting this in the above equation, we get \[{{x}^{2}}+4x-2x-2xr+1+2r=0\] .
\[\Rightarrow {{x}^{2}}+2x-2xr+1+2r=0\] \[(2)\]
The above quadratic equation will have equal roots because the circle intersects the parabola.
We know that when the quadratic equation of the form \[a{{x}^{2}}+bx+c=0\] has equal roots, we have \[{{b}^{2}}-4ac=0\] .
Substituting \[b=2-2r,c=1+2r\] from equation \[(2)\] to the above formula, we get \[{{(2-2r)}^{2}}=4(1+2r)\] .
On further solving this equation, we get
\[\begin{align}
& \Rightarrow 4+4{{r}^{2}}-8r=4+8r \\
& \Rightarrow 4{{r}^{2}}-16r=0 \\
& \Rightarrow 4r(r-4)=0 \\
& \Rightarrow r=0,r=4 \\
\end{align}\]
But the radius of the circle can’t be 0, so, the required answer is \[r=4\] .
Hence, the correct answer is 4.
Note: We can’t solve the question without the fact that the circle passes through the focus of the parabola and touches the parabola at some point. Also, one must know that a circle with 0 radius is just a point.
Complete step by step answer:
We have the equation of parabola as ${{y}^{2}}=4x $.
We want to find the radius of the largest circle which passes through the focus of the parabola.
We know the focus of the parabola of the form \[{{y}^{2}}=4ax\] is \[(a,0)\] .
Thus, the focus of the parabola \[{{y}^{2}}=4x\] is \[(1,0)\] .

As we want the largest circle contained in parabola \[{{y}^{2}}=4x\] and the circle passes through focus of parabola, the centre of the circle lies on \[x\] -axis.
Let’s assume that the centre of the circle is \[(h,0)\] .
Let the radius of the circle be \[r\] .
As the circle passes through \[(1,0)\] , we have \[h=1+r\] . \[(1)\]
We know the equation of circle passing through the point \[(h,k)\] is of the form \[{{(x-h)}^{2}}+{{(y-k)}^{2}}={{r}^{2}}\] .
So, the equation of our circle is \[{{(x-h)}^{2}}+{{y}^{2}}={{r}^{2}}\]
Substituting the value of \[h\] from equation \[(1)\] , we get \[{{(x-1-r)}^{2}}+{{y}^{2}}={{r}^{2}}\] .
\[\Rightarrow {{x}^{2}}+{{r}^{2}}+1-2x-2xr+2r+{{y}^{2}}={{r}^{2}}\]
\[\Rightarrow {{x}^{2}}+{{y}^{2}}-2x-2xr+1+2r=0\]
But, we know \[{{y}^{2}}=4x\] . Substituting this in the above equation, we get \[{{x}^{2}}+4x-2x-2xr+1+2r=0\] .
\[\Rightarrow {{x}^{2}}+2x-2xr+1+2r=0\] \[(2)\]
The above quadratic equation will have equal roots because the circle intersects the parabola.
We know that when the quadratic equation of the form \[a{{x}^{2}}+bx+c=0\] has equal roots, we have \[{{b}^{2}}-4ac=0\] .
Substituting \[b=2-2r,c=1+2r\] from equation \[(2)\] to the above formula, we get \[{{(2-2r)}^{2}}=4(1+2r)\] .
On further solving this equation, we get
\[\begin{align}
& \Rightarrow 4+4{{r}^{2}}-8r=4+8r \\
& \Rightarrow 4{{r}^{2}}-16r=0 \\
& \Rightarrow 4r(r-4)=0 \\
& \Rightarrow r=0,r=4 \\
\end{align}\]
But the radius of the circle can’t be 0, so, the required answer is \[r=4\] .
Hence, the correct answer is 4.
Note: We can’t solve the question without the fact that the circle passes through the focus of the parabola and touches the parabola at some point. Also, one must know that a circle with 0 radius is just a point.
Recently Updated Pages
JEE Main Chemistry Question Paper PDF Download with Answer Key

JEE Main 2023 (January 30th Shift 1) Physics Question Paper with Answer Key

JEE Main 2023 (January 25th Shift 1) Physics Question Paper with Answer Key

JEE Main 2023 (February 1st Shift 2) Chemistry Question Paper with Answer Key

JEE Main 2022 (June 29th Shift 1) Chemistry Question Paper with Answer Key

JEE Main 2022 (June 27th Shift 2) Chemistry Question Paper with Answer Key

Trending doubts
Learn About Angle Of Deviation In Prism: JEE Main Physics 2025

JEE Main Login 2045: Step-by-Step Instructions and Details

Radius of the largest circle which passes through -class-11-maths-JEE_Main

JEE Main Exam Marking Scheme: Detailed Breakdown of Marks and Negative Marking

Collision - Important Concepts and Tips for JEE

Ideal and Non-Ideal Solutions Raoult's Law - JEE

Other Pages
NCERT Solutions for Class 11 Maths In Hindi Chapter 10 Straight Lines

Free Radical Substitution Mechanism of Alkanes for JEE Main 2025

Current Loop as Magnetic Dipole and Its Derivation for JEE

An aeroplane left 50 minutes later than its schedu-class-11-maths-JEE_Main

JEE Main 2023 April 6 Shift 1 Question Paper with Answer Keys & Solutions

JEE Main 2023 January 30 Shift 2 Question Paper with Answer Keys & Solutions




