
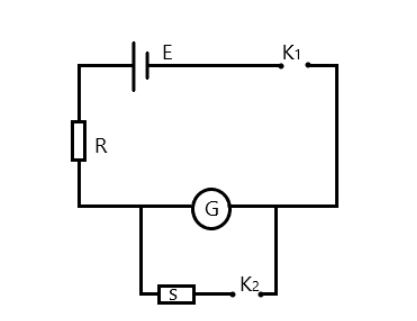
In an experiment to determine the resistance of a galvanometer by half deflection method, the circuit shown is used. In one set of readings, if \[R = 10\Omega \] and \[S = 4\Omega \], then the resistance of the galvanometer is:
(A) \[\dfrac{{20}}{3}\Omega \]
(B) \[\dfrac{{40}}{3}\Omega \]
(C) \[\dfrac{{50}}{3}\Omega \]
(D) \[\dfrac{{70}}{3}\Omega \]
Answer
165.9k+ views
Hint: In half deflection method, the value of the resistance across the resistor is such that the deflection made will be half that of the current when the resistance was disconnected. The current is directly proportional to the deflection of a galvanometer pointer.
Formula used: In this solution we will be using the following formulae;
\[G = \dfrac{{RS}}{{R - S}}\] where \[G\] is the resistance of the galvanometer, \[R\] is the resistance in the main circuit and \[S\] is the resistance across the galvanometer
Complete step by step solution:
Generally, the formula using half deflection method the resistance of a galvanometer is given as
\[G = \dfrac{{RS}}{{R - S}}\] where \[G\] is the resistance of the galvanometer, \[R\] is the resistance in the main circuit and \[S\] is the resistance across the galvanometer
Hence, by inserting known values, we have
\[G = \dfrac{{10\left( 4 \right)}}{{10 - 4}} = \dfrac{{40}}{6}\Omega \]
\[ \Rightarrow G = \dfrac{{20}}{3}\Omega \]
Hence, the correct option is A
Note: For clarity, the formula used can be proven as follows:
First, let’s assume the key \[{K_1}\] is the only closed key. In this case the current flowing through the circuit, and hence through \[G\] will be
\[{I_G} = \dfrac{E}{{R + G}}\]
Generally, the deflection shown in the galvanometer is proportional to the current flowing through it. Hence,
\[{I_G} = k\theta \]
Then
\[\dfrac{S}{{S + G}}I = \dfrac{{k\theta }}{2}\]
Now, assuming we close the key \[{K_2}\], it can be proven that the current flowing through the galvanometer becomes
\[I{'_G} = \dfrac{S}{{S + G}}I\]where\[I\] is the new current flowing through the main circuit, hence the current flowing through \[R\].
In the half deflection method, the value of S is adjusted such that the deflection is half of the original value when the key \[{K_2}\] was not closed.
Thus,
\[I{'_G} = \dfrac{{k\theta }}{2}\].
\[ \Rightarrow \dfrac{S}{{S + G}}I = \dfrac{{k\theta }}{2}\]
Dividing equation above by \[\dfrac{S}{{S + G}}I = \dfrac{{k\theta }}{2}\], and simplifying, we have
\[\dfrac{{SI(R + G)}}{{E(S + G)}} = \dfrac{1}{2}\]
Now, the equivalent resistance of the circuit is
\[{R_{eq}} = R + \dfrac{{SG}}{{S + G}}\]. Then the current would be
\[I = \dfrac{E}{{{R_{eq}}}} = \dfrac{E}{{R + \dfrac{{SG}}{{S + G}}}}\]
Then substituting into \[\dfrac{{SI(R + G)}}{{E(S + G)}} = \dfrac{1}{2}\] and then simplifying to make \[G\] subject, we have
\[G = \dfrac{{RS}}{{R - S}}\]
Formula used: In this solution we will be using the following formulae;
\[G = \dfrac{{RS}}{{R - S}}\] where \[G\] is the resistance of the galvanometer, \[R\] is the resistance in the main circuit and \[S\] is the resistance across the galvanometer
Complete step by step solution:
Generally, the formula using half deflection method the resistance of a galvanometer is given as
\[G = \dfrac{{RS}}{{R - S}}\] where \[G\] is the resistance of the galvanometer, \[R\] is the resistance in the main circuit and \[S\] is the resistance across the galvanometer
Hence, by inserting known values, we have
\[G = \dfrac{{10\left( 4 \right)}}{{10 - 4}} = \dfrac{{40}}{6}\Omega \]
\[ \Rightarrow G = \dfrac{{20}}{3}\Omega \]
Hence, the correct option is A
Note: For clarity, the formula used can be proven as follows:
First, let’s assume the key \[{K_1}\] is the only closed key. In this case the current flowing through the circuit, and hence through \[G\] will be
\[{I_G} = \dfrac{E}{{R + G}}\]
Generally, the deflection shown in the galvanometer is proportional to the current flowing through it. Hence,
\[{I_G} = k\theta \]
Then
\[\dfrac{S}{{S + G}}I = \dfrac{{k\theta }}{2}\]
Now, assuming we close the key \[{K_2}\], it can be proven that the current flowing through the galvanometer becomes
\[I{'_G} = \dfrac{S}{{S + G}}I\]where\[I\] is the new current flowing through the main circuit, hence the current flowing through \[R\].
In the half deflection method, the value of S is adjusted such that the deflection is half of the original value when the key \[{K_2}\] was not closed.
Thus,
\[I{'_G} = \dfrac{{k\theta }}{2}\].
\[ \Rightarrow \dfrac{S}{{S + G}}I = \dfrac{{k\theta }}{2}\]
Dividing equation above by \[\dfrac{S}{{S + G}}I = \dfrac{{k\theta }}{2}\], and simplifying, we have
\[\dfrac{{SI(R + G)}}{{E(S + G)}} = \dfrac{1}{2}\]
Now, the equivalent resistance of the circuit is
\[{R_{eq}} = R + \dfrac{{SG}}{{S + G}}\]. Then the current would be
\[I = \dfrac{E}{{{R_{eq}}}} = \dfrac{E}{{R + \dfrac{{SG}}{{S + G}}}}\]
Then substituting into \[\dfrac{{SI(R + G)}}{{E(S + G)}} = \dfrac{1}{2}\] and then simplifying to make \[G\] subject, we have
\[G = \dfrac{{RS}}{{R - S}}\]
Recently Updated Pages
Classification of Elements and Periodicity in Properties | Trends, Notes & FAQs

JEE Main 2021 July 25 Shift 1 Question Paper with Answer Key

JEE Main 2021 July 22 Shift 2 Question Paper with Answer Key

Transistor as Amplifier: Working, Diagram, Uses & Questions

Moving Charges and Magnetism: Laws, Formulas & Applications

Environmental Chemistry Chapter for JEE Main Chemistry

Trending doubts
JEE Main 2025 Session 2: Application Form (Out), Exam Dates (Released), Eligibility, & More

Combination of Capacitors - In Parallel and Series for JEE

Electric field due to uniformly charged sphere class 12 physics JEE_Main

Uniform Acceleration

Displacement-Time Graph and Velocity-Time Graph for JEE

JEE Main 2025: Derivation of Equation of Trajectory in Physics

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

Electrical Field of Charged Spherical Shell - JEE

JEE Advanced Weightage 2025 Chapter-Wise for Physics, Maths and Chemistry

Learn About Angle Of Deviation In Prism: JEE Main Physics 2025

Wheatstone Bridge for JEE Main Physics 2025

Degree of Dissociation and Its Formula With Solved Example for JEE




