
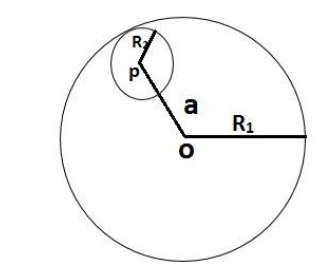
Consider a uniform spherical charge distribution of radius ${R_1}$ centred at the origin O. In this distribution a spherical cavity of radius${R_2}$, centred at P with distance $OP = a = {R_1} = {R_2}$ is made. If the electric field inside the cavity at position $\vec r$ is $\vec E\left( {\vec r} \right)$, then the correct statement is
(A) $\vec E$ is uniform, its magnitude is independent of ${R_2}$ but its direction depends on $\vec r$
(B) $\vec E$ is uniform, its magnitude is dependent of ${R_2}$ but its direction depends on $\vec r$
(C) $\vec E$ is uniform, its magnitude is independent of $a$ but its direction depends on $\vec a$
(D) $\vec E$ is uniform and both its magnitude and direction depend on $\vec a$.
Answer
173.4k+ views
Hint: Due to the larger sphere without the cavity and a smaller sphere with opposite charge density, the principle of superposition of electric fields can be applied. We need to apply Gauss’s Law to get the final answer.
Complete Step by Step Solution: Every charged particle creates an electric field in the universe in the space surrounding it. The electric field created due to the charge is independent of the presence or absence of all other charges. The electric field created can be calculated with the help of Coulomb’s law. The principle of superposition allows for the combination of two or more electric fields.
Superposition Principle gives the total force on a given charge due to any number of point charges acting on it. The principle of superposition states that every charge in space creates an electric field at a point independent of the presence of other charges in that medium. The resultant electric field is a vector sum of the electric field due to individual charges.
Since it has been given that, a uniform spherical charge distribution centred at the origin O has a radius ${R_1}$. In this distribution a spherical cavity of radius${R_2}$, centred at P with distance $OP = a = {R_1} = {R_2}$ is made and the electric field inside the cavity at position $\vec r$ is $\vec E\left( {\vec r} \right)$.
The problem can be considered as a superposition of electric fields due to the larger sphere without the cavity and a smaller sphere with opposite charge density.
By application of Gauss’ Law, for an internal point inside the spherical charge distribution, we have,
$\vec E\left( {\vec r} \right) = \dfrac{{\rho r}}{{3{ \in _r}}}$ where $\rho $ is the density.
By principle of superposition, $\vec E = {\vec E_1} + {\vec E_2}$.
$\dfrac{\rho }{{3{ \in _0}}}O\vec A + \dfrac{\rho }{{3{ \in _0}}}\vec AP + \dfrac{\rho }{{3{ \in _0}}}\left( {O\vec A + \vec AP} \right)$
We can write,
$\vec E = \dfrac{\rho }{{3{ \in _0}}}O\vec A = \dfrac{\rho }{{3{ \in _0}}}\vec a$
Hence, $\vec E$ is uniform and both its magnitude and direction depend on $\vec a$.
The correct answer is Option D.
Note: Gauss Law states that the total electric flux out of a closed surface is equal to the charge enclosed divided by the permittivity. The electric flux in an area is defined as the electric field multiplied by the area of the surface projected in a plane and perpendicular to the field.
Complete Step by Step Solution: Every charged particle creates an electric field in the universe in the space surrounding it. The electric field created due to the charge is independent of the presence or absence of all other charges. The electric field created can be calculated with the help of Coulomb’s law. The principle of superposition allows for the combination of two or more electric fields.
Superposition Principle gives the total force on a given charge due to any number of point charges acting on it. The principle of superposition states that every charge in space creates an electric field at a point independent of the presence of other charges in that medium. The resultant electric field is a vector sum of the electric field due to individual charges.
Since it has been given that, a uniform spherical charge distribution centred at the origin O has a radius ${R_1}$. In this distribution a spherical cavity of radius${R_2}$, centred at P with distance $OP = a = {R_1} = {R_2}$ is made and the electric field inside the cavity at position $\vec r$ is $\vec E\left( {\vec r} \right)$.
The problem can be considered as a superposition of electric fields due to the larger sphere without the cavity and a smaller sphere with opposite charge density.
By application of Gauss’ Law, for an internal point inside the spherical charge distribution, we have,
$\vec E\left( {\vec r} \right) = \dfrac{{\rho r}}{{3{ \in _r}}}$ where $\rho $ is the density.
By principle of superposition, $\vec E = {\vec E_1} + {\vec E_2}$.
$\dfrac{\rho }{{3{ \in _0}}}O\vec A + \dfrac{\rho }{{3{ \in _0}}}\vec AP + \dfrac{\rho }{{3{ \in _0}}}\left( {O\vec A + \vec AP} \right)$
We can write,
$\vec E = \dfrac{\rho }{{3{ \in _0}}}O\vec A = \dfrac{\rho }{{3{ \in _0}}}\vec a$
Hence, $\vec E$ is uniform and both its magnitude and direction depend on $\vec a$.
The correct answer is Option D.
Note: Gauss Law states that the total electric flux out of a closed surface is equal to the charge enclosed divided by the permittivity. The electric flux in an area is defined as the electric field multiplied by the area of the surface projected in a plane and perpendicular to the field.
Recently Updated Pages
JEE Main Mock Test 2025-26: Chapter-Wise Practice Papers

JEE Main Electromagnetic Waves Mock Test 2025-26 | Free Practice Online

JEE Main 2025-26 Electronic Devices Mock Test: Free Practice Online

JEE Main Mock Test 2025-26: Current Electricity Practice Online

JEE Main 2025-26 Electrostatics Mock Test – Free Practice Online

JEE Main 2025-26 Units and Measurements Mock Test Online

Trending doubts
JEE Main 2025 Session 2: Application Form (Out), Exam Dates (Released), Eligibility, & More

Displacement-Time Graph and Velocity-Time Graph for JEE

Uniform Acceleration

Electric field due to uniformly charged sphere class 12 physics JEE_Main

JEE Main 2025: Derivation of Equation of Trajectory in Physics

Learn About Angle Of Deviation In Prism: JEE Main Physics 2025

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

Instantaneous Velocity - Formula based Examples for JEE

JEE Advanced Weightage 2025 Chapter-Wise for Physics, Maths and Chemistry

Essential Derivations for CBSE Class 12 Physics: Stepwise & PDF Solutions

Electron Gain Enthalpy and Electron Affinity for JEE

Wheatstone Bridge for JEE Main Physics 2025




