
What is the area under the curve $y=|x|+|x-1|$ between$x=0$ and $x=1$.
A. $\dfrac{1}{2}$
B. $1$
C. $\dfrac{3}{2}$
D. $2$
Answer
219.3k+ views
Hint: To find the area under the curve $y=|x|+|x-1|$ between$x=0$ and $x=1$,we will write the value of $x$ in the given interval and determine the equation of the curve.
Then we will integrate it using limits by taking lower limit $x=0$ and upper limit $x=1$and determine the area.
Formula Used:The limits of integration of a function can be calculated by $\begin{align}
& \int\limits_{b}^{a}{f(x).dx}=\left[ f(x) \right]_{b}^{a} \\
& =f(a)-f(b)
\end{align}$
Complete step by step solution:We are given an equation of curve$y=|x|+|x-1|$ and we have to find the area enclosed by it in between the interval $x=0$ and $x=1$.
For the interval\[x\ge 0\],
$|x|=x$
And for the interval \[x\le 1\],
$|x-1|=-(x-1)$
The equation will be $y=x-(x-1)$
Now we will integrate it taking $x=0$as lower limit and $x=1$as upper limit.
\[Area=\int\limits_{0}^{1}{x.dx}-\int\limits_{0}^{1}{(x-1)dx}\]
\[=\left[ \dfrac{{{x}^{2}}}{2} \right]_{0}^{1}-\left[ \dfrac{{{x}^{2}}}{2}-x \right]_{0}^{1}\]
Applying the limits,
\[=\left[ \dfrac{1}{2}-\dfrac{0}{2} \right]-\left[ \left( \dfrac{1}{2}-1 \right)-\left( \dfrac{0}{2}-0 \right) \right]\]
\[=\dfrac{1}{2}-\left( \dfrac{1}{2}-1 \right)\]
\[=1\]square unit.
The area under the curve $y=|x|+|x-1|$ between $x=0$ and $x=1$ is $1$ square units.
Thus, the area under the curve $y=|x|+|x-1|$ between$x=0$ and $x=1$
Option ‘D’ is correct
Note:We can also find the area under the curve by another method. In this method we will simplify the equation of the curve first.
The equation of the curve is .
Now we will draw the graph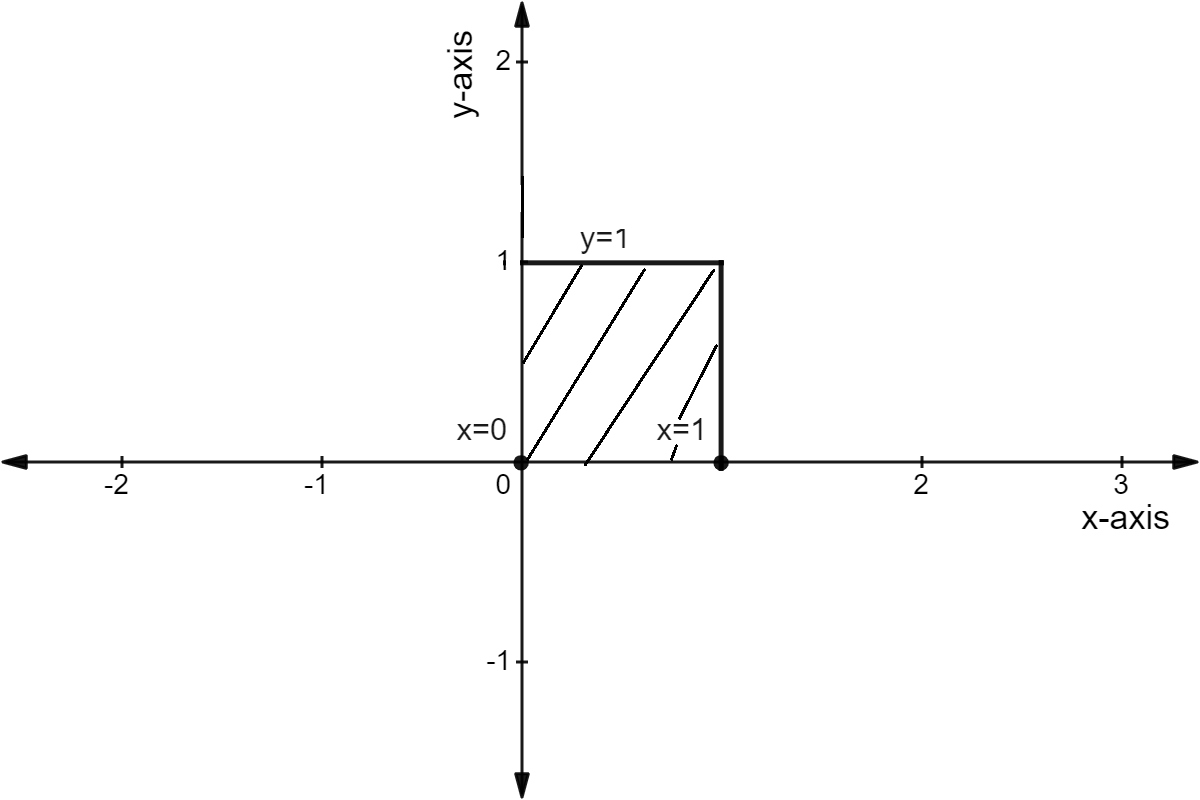
We can see that a quadrilateral is formed on the graph of the curve between the interval l and . The quadrilateral formed is a square because each of the side is of length of unit .
We will calculate the area under the curve by finding the area of the square. As we know the formula of the area of the square is , we will use it.
1 square units.
.
Then we will integrate it using limits by taking lower limit $x=0$ and upper limit $x=1$and determine the area.
Formula Used:The limits of integration of a function can be calculated by $\begin{align}
& \int\limits_{b}^{a}{f(x).dx}=\left[ f(x) \right]_{b}^{a} \\
& =f(a)-f(b)
\end{align}$
Complete step by step solution:We are given an equation of curve$y=|x|+|x-1|$ and we have to find the area enclosed by it in between the interval $x=0$ and $x=1$.
For the interval\[x\ge 0\],
$|x|=x$
And for the interval \[x\le 1\],
$|x-1|=-(x-1)$
The equation will be $y=x-(x-1)$
Now we will integrate it taking $x=0$as lower limit and $x=1$as upper limit.
\[Area=\int\limits_{0}^{1}{x.dx}-\int\limits_{0}^{1}{(x-1)dx}\]
\[=\left[ \dfrac{{{x}^{2}}}{2} \right]_{0}^{1}-\left[ \dfrac{{{x}^{2}}}{2}-x \right]_{0}^{1}\]
Applying the limits,
\[=\left[ \dfrac{1}{2}-\dfrac{0}{2} \right]-\left[ \left( \dfrac{1}{2}-1 \right)-\left( \dfrac{0}{2}-0 \right) \right]\]
\[=\dfrac{1}{2}-\left( \dfrac{1}{2}-1 \right)\]
\[=1\]square unit.
The area under the curve $y=|x|+|x-1|$ between $x=0$ and $x=1$ is $1$ square units.
Thus, the area under the curve $y=|x|+|x-1|$ between$x=0$ and $x=1$
Option ‘D’ is correct
Note:We can also find the area under the curve by another method. In this method we will simplify the equation of the curve first.
The equation of the curve is .
Now we will draw the graph

We can see that a quadrilateral is formed on the graph of the curve between the interval l and . The quadrilateral formed is a square because each of the side is of length of unit .
We will calculate the area under the curve by finding the area of the square. As we know the formula of the area of the square is , we will use it.
1 square units.
.
Recently Updated Pages
The angle of depression of the top and the bottom of class 10 maths JEE_Main

Find the value of sin 50 circ sin 70 circ + sin 10 class 10 maths JEE_Main

The amount of work in a leather factory is increased class 10 maths JEE_Main

The side BC of a triangle ABC is bisected at D O is class 10 maths JEE_Main

The circumference of the base of a 24 m high conical class 10 maths JEE_Main

Mutually Exclusive vs Independent Events: Key Differences Explained

Trending doubts
JEE Main 2026: Application Form Open, Exam Dates, Syllabus, Eligibility & Question Papers

JEE Main Syllabus 2026: Download Detailed Subject-wise PDF

JEE Main Previous Year Question Papers (2014–2025) with Answer Keys and Solutions

Exothermic Reactions: Real-Life Examples, Equations, and Uses

Marks vs Percentile JEE Mains 2026: Calculate Percentile Marks

Understanding Newton’s Laws of Motion

Other Pages
NCERT Solutions For Class 10 Maths Chapter 12 Surface Area And Volume

NCERT Solutions for Class 10 Maths Chapter Chapter 13 Statistics

NCERT Solutions for Class 10 Maths Chapter 11 Areas Related to Circles 2025-26

Pregnancy Week and Due Date Calculator: Find How Far Along You Are

Complete List of Class 10 Maths Formulas (Chapterwise)

NCERT Solutions for Class 10 Maths Chapter 15 Probability




