
An inductor and resistor are connected in series with an AC source. In this circuit,
The current and the PD across resistance lead the PD across the inductance.
(A) The current and the PD across the resistance lag behind the PD across the inductance by angle $\dfrac{\pi }{2}$
(B) The current and the PD across the resistance lag behind the PD across the inductance by an angle $\pi $
(C) The PD across the resistance lags behind the PD across the inductance by an angle (D)$\dfrac{\pi }{2}$ but the current in resistance leads the PD across the inductance by $\dfrac{\pi }{2}$.
Answer
160.2k+ views
Hint Find the impedance for series resistance and inductor AC circuit then, draw the phasor diagram of series inductance and resistance series AC circuit. In the phasor diagram, draw the voltage across resistance and also draw the voltage across inductance. If the angle of voltage across inductance is greater then it leads the voltage across resistance.
Step by Step Solution
Let the resistance and inductance be R and L respectively
Construct a series L-R AC circuit
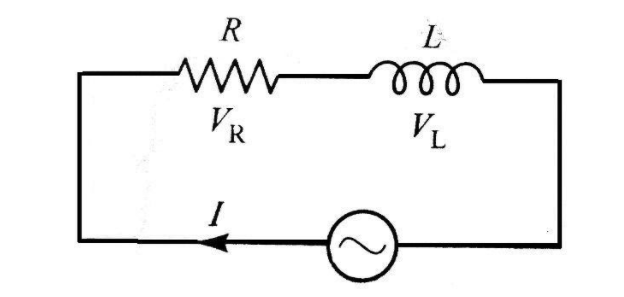
Now, we get
${V_{net}} = {\vec V_L} + {\vec V_R}$
By taking magnitude
\[
\left| {{{\vec V}_{net}}} \right| = \sqrt {({V^2}_L + {V^2}_R)} \\
\left| {{{\vec V}_{net}}} \right| = \sqrt {({i^2}{X^2}_L + {i^2}{R^2})} \\
\\
\]
By taking ${i^2}$ common
\[\left| {{{\vec V}_{net}}} \right| = i\sqrt {({X^2}_L + {R^2})} \]
To calculate the impedance let impedance be $Z$
$Z = \dfrac{V}{i} = \sqrt {({X_L}^2 + {R^2})} $
Because, ${X_L} = \omega L$ we get
$Z = \sqrt {({\omega ^2}{L^2} + {R^2})} $
This is the impedance for series L-R AC circuit
Now, draw the phasor diagram for series L-R AC circuit
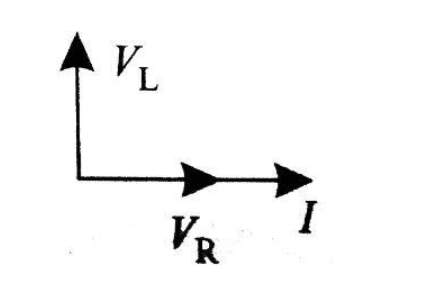
$
\tan \varphi = \dfrac{{{V_L}}}{{{V_R}}} \\
\tan \varphi = \dfrac{{i{X_L}}}{{iR}} \\
\\
$
Now, we get
$\varphi = {\tan ^{ - 1}}\left( {\dfrac{{{X_L}}}{R}} \right)$
Therefore, after seeing the phasor diagram we can easily conclude that potential difference across inductance leads the current and potential difference across resistance by an angle $\dfrac{\pi }{2}$
Hence, option (B) is the correct answer.
Note resistance is the measure of the opposition of current in the circuit. It is denoted by R. It is measured in ohms $(\Omega )$.
Inductance is the property of a conductor to oppose the flow of electric current through it. The flow of current makes a magnetic field around the conductor. It is denoted by L. It is measured in Henry $(H)$.
Step by Step Solution
Let the resistance and inductance be R and L respectively
Construct a series L-R AC circuit

Now, we get
${V_{net}} = {\vec V_L} + {\vec V_R}$
By taking magnitude
\[
\left| {{{\vec V}_{net}}} \right| = \sqrt {({V^2}_L + {V^2}_R)} \\
\left| {{{\vec V}_{net}}} \right| = \sqrt {({i^2}{X^2}_L + {i^2}{R^2})} \\
\\
\]
By taking ${i^2}$ common
\[\left| {{{\vec V}_{net}}} \right| = i\sqrt {({X^2}_L + {R^2})} \]
To calculate the impedance let impedance be $Z$
$Z = \dfrac{V}{i} = \sqrt {({X_L}^2 + {R^2})} $
Because, ${X_L} = \omega L$ we get
$Z = \sqrt {({\omega ^2}{L^2} + {R^2})} $
This is the impedance for series L-R AC circuit
Now, draw the phasor diagram for series L-R AC circuit

$
\tan \varphi = \dfrac{{{V_L}}}{{{V_R}}} \\
\tan \varphi = \dfrac{{i{X_L}}}{{iR}} \\
\\
$
Now, we get
$\varphi = {\tan ^{ - 1}}\left( {\dfrac{{{X_L}}}{R}} \right)$
Therefore, after seeing the phasor diagram we can easily conclude that potential difference across inductance leads the current and potential difference across resistance by an angle $\dfrac{\pi }{2}$
Hence, option (B) is the correct answer.
Note resistance is the measure of the opposition of current in the circuit. It is denoted by R. It is measured in ohms $(\Omega )$.
Inductance is the property of a conductor to oppose the flow of electric current through it. The flow of current makes a magnetic field around the conductor. It is denoted by L. It is measured in Henry $(H)$.
Recently Updated Pages
JEE Main 2021 July 25 Shift 1 Question Paper with Answer Key

JEE Main 2021 July 22 Shift 2 Question Paper with Answer Key

JEE Atomic Structure and Chemical Bonding important Concepts and Tips

JEE Amino Acids and Peptides Important Concepts and Tips for Exam Preparation

Chemical Properties of Hydrogen - Important Concepts for JEE Exam Preparation

JEE General Topics in Chemistry Important Concepts and Tips

Trending doubts
JEE Main 2025 Session 2: Application Form (Out), Exam Dates (Released), Eligibility, & More

JEE Main 2025: Derivation of Equation of Trajectory in Physics

Electric Field Due to Uniformly Charged Ring for JEE Main 2025 - Formula and Derivation

Electric field due to uniformly charged sphere class 12 physics JEE_Main

Displacement-Time Graph and Velocity-Time Graph for JEE

Uniform Acceleration

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

JEE Advanced 2025: Dates, Registration, Syllabus, Eligibility Criteria and More

JEE Advanced Weightage 2025 Chapter-Wise for Physics, Maths and Chemistry

Degree of Dissociation and Its Formula With Solved Example for JEE

Free Radical Substitution Mechanism of Alkanes for JEE Main 2025

If a wire of resistance R is stretched to double of class 12 physics JEE_Main




