
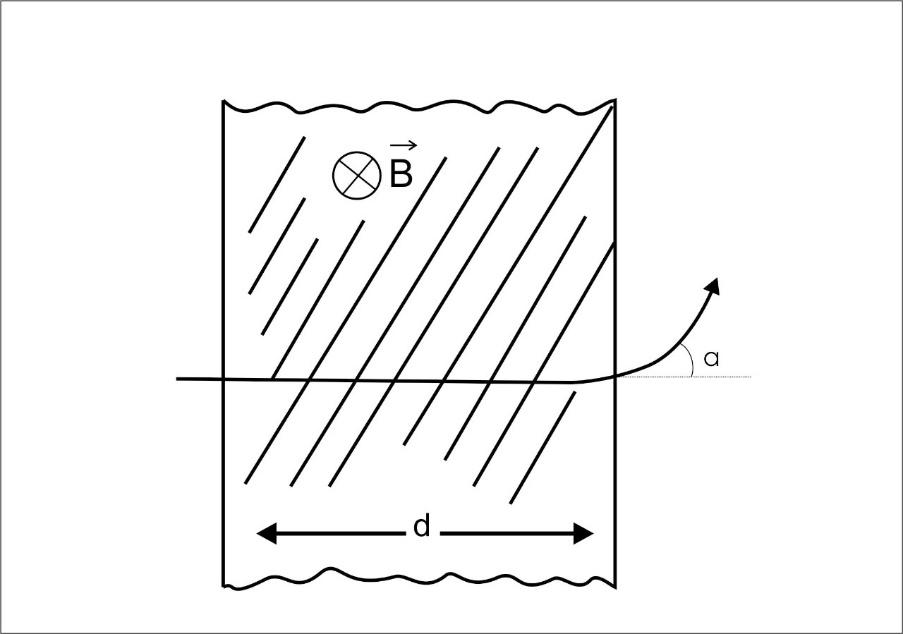
A proton (mass m) accelerated by a potential difference V files through a uniform transverse magnetic field B. The field occupies a region of space by width ‘d’. If $\alpha $ be the angle of deviations of proton from initial direction of motion (see fig), the value of $\sin \alpha $ will be:
A) $Bd\sqrt {\dfrac{q}{{2mV}}} $
B) $\dfrac{B}{d}\sqrt {\dfrac{{qd}}{{mV}}} $
C) $qV\sqrt {\dfrac{{Bd}}{{2m}}} $
D) $\dfrac{B}{d}\sqrt {\dfrac{q}{{2mV}}} $
Answer
222.9k+ views
Hint: In this question, first we have to calculate energy of proton $E$ in the term of $v$ , and then have to find the magnetic force $F$. From the given figure we can easily find that $\sin \alpha = \dfrac{d}{R}$ . After putting the value of $R$ we can easily find the value of $\sin \alpha $.
Complete step by step answer:
In this question, A proton (mass m) is accelerated by a potential difference V files through a uniform transverse magnetic field B, and the field occupies a region of space by width ‘$d$ ’. Here, $\alpha $ be the angle of deviation of proton from initial direction of motion .we need to calculate, the value of $\sin \alpha $.
Given that,
$m = $ Mass of proton
$V = $ Potential difference
$v = $ Velocity of proton
$e = $ Charge on proton
$d = $ The field occupies a region of space of width.
$R = $ The radius of circle
$\alpha = $ Angle of deviation
Now, first we have to find the energy of proton,
We know that,
$ E = \dfrac{1}{2}m{v^2} = eV$
Hence,
$\Rightarrow v = \sqrt {\dfrac{{2eV}}{m}} $
Now find the magnetic force, we know that magnetic force can be written as,
\[\Rightarrow F = e\left( {\overrightarrow v \times \overrightarrow B } \right)\]
$ \Rightarrow \dfrac{{m{v^2}}}{R} \\
\Rightarrow R = \dfrac{{mv}}{{eB}} \\ $
We know that,
$\Rightarrow \sin \alpha = \dfrac{d}{R}$
On putting the value of$R$, we get
$\Rightarrow \sin \alpha = \dfrac{{deB}}{{mv}} \\
\Rightarrow \sin \alpha = \dfrac{{deB}}{m}\sqrt {\dfrac{m}{{2eV}}} \\
\Rightarrow \sin \alpha = Bd\sqrt {\dfrac{e}{{2mV}}} \\ $
$e$ can be written as $q$, which is the symbol of charge, thus the equation become, $\sin \alpha = Bd\sqrt {\dfrac{q}{{2mV}}} $
Therefore, the correct option is A.
Note: As we know that the force is the vector quantity and the cross product of the velocity and the magnetic field provide the vector quantity. And we know the correct value of $R$ is obtained as $\sin \alpha = \dfrac{d}{R}$.
Complete step by step answer:
In this question, A proton (mass m) is accelerated by a potential difference V files through a uniform transverse magnetic field B, and the field occupies a region of space by width ‘$d$ ’. Here, $\alpha $ be the angle of deviation of proton from initial direction of motion .we need to calculate, the value of $\sin \alpha $.
Given that,
$m = $ Mass of proton
$V = $ Potential difference
$v = $ Velocity of proton
$e = $ Charge on proton
$d = $ The field occupies a region of space of width.
$R = $ The radius of circle
$\alpha = $ Angle of deviation
Now, first we have to find the energy of proton,
We know that,
$ E = \dfrac{1}{2}m{v^2} = eV$
Hence,
$\Rightarrow v = \sqrt {\dfrac{{2eV}}{m}} $
Now find the magnetic force, we know that magnetic force can be written as,
\[\Rightarrow F = e\left( {\overrightarrow v \times \overrightarrow B } \right)\]
$ \Rightarrow \dfrac{{m{v^2}}}{R} \\
\Rightarrow R = \dfrac{{mv}}{{eB}} \\ $
We know that,
$\Rightarrow \sin \alpha = \dfrac{d}{R}$
On putting the value of$R$, we get
$\Rightarrow \sin \alpha = \dfrac{{deB}}{{mv}} \\
\Rightarrow \sin \alpha = \dfrac{{deB}}{m}\sqrt {\dfrac{m}{{2eV}}} \\
\Rightarrow \sin \alpha = Bd\sqrt {\dfrac{e}{{2mV}}} \\ $
$e$ can be written as $q$, which is the symbol of charge, thus the equation become, $\sin \alpha = Bd\sqrt {\dfrac{q}{{2mV}}} $
Therefore, the correct option is A.
Note: As we know that the force is the vector quantity and the cross product of the velocity and the magnetic field provide the vector quantity. And we know the correct value of $R$ is obtained as $\sin \alpha = \dfrac{d}{R}$.
Recently Updated Pages
JEE General Topics in Chemistry Important Concepts and Tips

JEE Extractive Metallurgy Important Concepts and Tips for Exam Preparation

JEE Atomic Structure and Chemical Bonding important Concepts and Tips

JEE Amino Acids and Peptides Important Concepts and Tips for Exam Preparation

Electricity and Magnetism Explained: Key Concepts & Applications

JEE Energetics Important Concepts and Tips for Exam Preparation

Trending doubts
JEE Main 2026: Application Form Open, Exam Dates, Syllabus, Eligibility & Question Papers

Derivation of Equation of Trajectory Explained for Students

Hybridisation in Chemistry – Concept, Types & Applications

Understanding the Angle of Deviation in a Prism

How to Convert a Galvanometer into an Ammeter or Voltmeter

Degree of Dissociation: Meaning, Formula, Calculation & Uses

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

Dual Nature of Radiation and Matter Class 12 Physics Chapter 11 CBSE Notes - 2025-26

Ideal and Non-Ideal Solutions Explained for Class 12 Chemistry

Understanding the Electric Field of a Uniformly Charged Ring

Understanding Atomic Structure for Beginners

Understanding Electromagnetic Waves and Their Importance




