
A long bar magnet of magnetic moment $6A{m^2}$ & $8A{m^2}$ can be fastened together with their axes horizontal and the centres in a vertical line about which the system is free to oscillate. Compare the time periods in the earth’s field when the axes of magnets are in the same direction, opposite direction and right angles.
A) $1:7:5$
B) $1:\sqrt 7 :\sqrt 5 $
C) $1:\sqrt 7 :\sqrt {\dfrac{7}{5}} $
D) $1:\sqrt {\dfrac{7}{5}} :\sqrt {\dfrac{{14}}{5}} $
Answer
172.5k+ views
Hint: To solve this problem, we have to consider the quantity magnetic moment as a vector and treat it as a vector when performing the addition operation on them. Different orientations of the magnetic moments of these two bar magnets with respect to each other will yield us different results.
Formula Used:
The time period of oscillation of bar magnet is –
$T = 2\pi \sqrt {\dfrac{I}{{mB}}} $
where $I$= moment of inertia, m = magnetic moment and B = magnetic field.
Complete step by step answer:
When a magnetic material is placed in an external magnetic field, it experiences a moment of force since equal and opposite forces act on both of the poles – North and South. This causes a moment of force which enables the magnetic material to orient itself along the direction of the external applied field.
Here, we can define a quantity called magnetic moment, which is a measure of the tendency of the magnetic material to re-arrange its poles along the direction of the external field.
Mathematically, the magnetic moment is measured as the product of current flowing around the poles and the area,
$M = I \times A$
The SI unit of magnetic moment is $A{m^2}$ and it is a vector quantity whose direction is from South pole to North pole of the magnet.
In the given problem, there are two bar magnets of magnetic moments ${m_1} = 6A{m^2}$ & ${m_2} = 8A{m^2}$. These bar magnets are placed in different orientations. Let us understand the combined magnetic moment in each orientation:
i) Same direction.
The two bar magnets are placed on one another, with North of one magnet placed over the North pole of the other and the same for South poles, as shown:
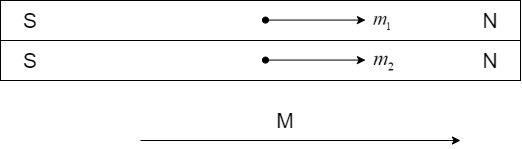
The net moment,
$\overrightarrow M = \overrightarrow {{m_1}} + \overrightarrow {{m_2}} $
Since the moments ${m_1}$ and ${m_2}$ are oriented in the same direction, the magnitude of the net moment is equal to the algebraic sum of the moments.
$M = {m_1} + {m_2}$
Substituting and adding,
$M = 6 + 8 = 14A{m^2}$
ii) Opposite direction.
The two bar magnets are placed on one another, with North of one magnet placed over the South pole of the other and vice-versa, as shown:
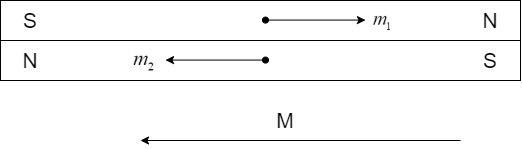
The net moment,
$\overrightarrow M = \overrightarrow {{m_1}} + \overrightarrow {{m_2}} $
Since the moments ${m_1}$ and ${m_2}$ are oriented in the opposite direction, the magnitude of the net moment is equal to the algebraic difference of the moments.
$M = {m_2} - {m_1}$
Substituting and adding,
$M = 8 - 6 = 2A{m^2}$
iii) Right angles
Here, the magnets are so arranged that the axis of one magnet is perpendicular to the axis of another.
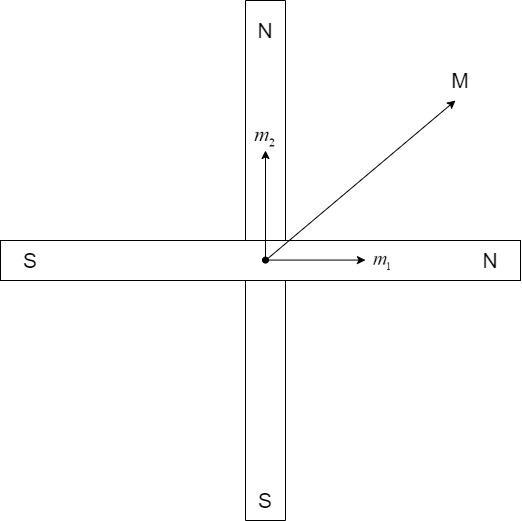
The net moment,
$\overrightarrow M = \overrightarrow {{m_1}} + \overrightarrow {{m_2}} $
Here, the moments are at right angles to each other. Hence, the magnitude of the vector M, is given by –
$M = \sqrt {m_1^2 + m_2^2} $
Substituting,
$M = \sqrt {{6^2} + {8^2}} = \sqrt {36 + 64} = \sqrt {100} = 10A{m^2}$
The time period of oscillation of bar magnet is –
$T = 2\pi \sqrt {\dfrac{I}{{mB}}} $
where $I$= moment of inertia, m = magnetic moment and B = magnetic field.
We can deduce that –
$T \propto \dfrac{1}{{\sqrt m }}$
Let us compare the time periods of the magnets in various orientations as:
Same: Opposite: Right angles = $\dfrac{1}{{\sqrt {14} }}:\dfrac{1}{{\sqrt 2 }}:\dfrac{1}{{\sqrt {10} }}$
$\Rightarrow \dfrac{1}{{\sqrt 2 \sqrt 7 }}:\dfrac{1}{{\sqrt 2 }}:\dfrac{1}{{\sqrt 5 \sqrt 2 }}$
$\Rightarrow \dfrac{1}{{\sqrt 7 }}:1:\dfrac{1}{{\sqrt 5 }}$
Multiplying the whole ratio by $\sqrt 7$, we get –
$\Rightarrow \dfrac{{\sqrt 7 }}{{\sqrt 7 }}:\sqrt 7 :\dfrac{{\sqrt 7 }}{{\sqrt 5 }}$
$\Rightarrow 1:\sqrt 7 :\sqrt {\dfrac{7}{5}}$
Hence, the correct option is Option C.
Note: In this problem, the magnitudes were computed directly based on the concept, but however, you can use the direct formula for magnitude of a vector.
If $\overrightarrow K = \overrightarrow A + \overrightarrow B$,
The magnitude of the sum, $\overrightarrow {\left| K \right|} = \sqrt {{A^2} + {B^2} + 2AB\cos \theta }$
where $\theta$= angle between the two vectors, A and B.
Formula Used:
The time period of oscillation of bar magnet is –
$T = 2\pi \sqrt {\dfrac{I}{{mB}}} $
where $I$= moment of inertia, m = magnetic moment and B = magnetic field.
Complete step by step answer:
When a magnetic material is placed in an external magnetic field, it experiences a moment of force since equal and opposite forces act on both of the poles – North and South. This causes a moment of force which enables the magnetic material to orient itself along the direction of the external applied field.
Here, we can define a quantity called magnetic moment, which is a measure of the tendency of the magnetic material to re-arrange its poles along the direction of the external field.
Mathematically, the magnetic moment is measured as the product of current flowing around the poles and the area,
$M = I \times A$
The SI unit of magnetic moment is $A{m^2}$ and it is a vector quantity whose direction is from South pole to North pole of the magnet.
In the given problem, there are two bar magnets of magnetic moments ${m_1} = 6A{m^2}$ & ${m_2} = 8A{m^2}$. These bar magnets are placed in different orientations. Let us understand the combined magnetic moment in each orientation:
i) Same direction.
The two bar magnets are placed on one another, with North of one magnet placed over the North pole of the other and the same for South poles, as shown:

The net moment,
$\overrightarrow M = \overrightarrow {{m_1}} + \overrightarrow {{m_2}} $
Since the moments ${m_1}$ and ${m_2}$ are oriented in the same direction, the magnitude of the net moment is equal to the algebraic sum of the moments.
$M = {m_1} + {m_2}$
Substituting and adding,
$M = 6 + 8 = 14A{m^2}$
ii) Opposite direction.
The two bar magnets are placed on one another, with North of one magnet placed over the South pole of the other and vice-versa, as shown:

The net moment,
$\overrightarrow M = \overrightarrow {{m_1}} + \overrightarrow {{m_2}} $
Since the moments ${m_1}$ and ${m_2}$ are oriented in the opposite direction, the magnitude of the net moment is equal to the algebraic difference of the moments.
$M = {m_2} - {m_1}$
Substituting and adding,
$M = 8 - 6 = 2A{m^2}$
iii) Right angles
Here, the magnets are so arranged that the axis of one magnet is perpendicular to the axis of another.

The net moment,
$\overrightarrow M = \overrightarrow {{m_1}} + \overrightarrow {{m_2}} $
Here, the moments are at right angles to each other. Hence, the magnitude of the vector M, is given by –
$M = \sqrt {m_1^2 + m_2^2} $
Substituting,
$M = \sqrt {{6^2} + {8^2}} = \sqrt {36 + 64} = \sqrt {100} = 10A{m^2}$
The time period of oscillation of bar magnet is –
$T = 2\pi \sqrt {\dfrac{I}{{mB}}} $
where $I$= moment of inertia, m = magnetic moment and B = magnetic field.
We can deduce that –
$T \propto \dfrac{1}{{\sqrt m }}$
Let us compare the time periods of the magnets in various orientations as:
Same: Opposite: Right angles = $\dfrac{1}{{\sqrt {14} }}:\dfrac{1}{{\sqrt 2 }}:\dfrac{1}{{\sqrt {10} }}$
$\Rightarrow \dfrac{1}{{\sqrt 2 \sqrt 7 }}:\dfrac{1}{{\sqrt 2 }}:\dfrac{1}{{\sqrt 5 \sqrt 2 }}$
$\Rightarrow \dfrac{1}{{\sqrt 7 }}:1:\dfrac{1}{{\sqrt 5 }}$
Multiplying the whole ratio by $\sqrt 7$, we get –
$\Rightarrow \dfrac{{\sqrt 7 }}{{\sqrt 7 }}:\sqrt 7 :\dfrac{{\sqrt 7 }}{{\sqrt 5 }}$
$\Rightarrow 1:\sqrt 7 :\sqrt {\dfrac{7}{5}}$
Hence, the correct option is Option C.
Note: In this problem, the magnitudes were computed directly based on the concept, but however, you can use the direct formula for magnitude of a vector.
If $\overrightarrow K = \overrightarrow A + \overrightarrow B$,
The magnitude of the sum, $\overrightarrow {\left| K \right|} = \sqrt {{A^2} + {B^2} + 2AB\cos \theta }$
where $\theta$= angle between the two vectors, A and B.
Recently Updated Pages
Sets, Relations, and Functions Mock Test 2025-26

Molarity vs Molality: Definitions, Formulas & Key Differences

Preparation of Hydrogen Gas: Methods & Uses Explained

Polymers in Chemistry: Definition, Types, Examples & Uses

P Block Elements: Definition, Groups, Trends & Properties for JEE/NEET

Order of Reaction in Chemistry: Definition, Formula & Examples

Trending doubts
JEE Main 2025 Session 2: Application Form (Out), Exam Dates (Released), Eligibility, & More

Displacement-Time Graph and Velocity-Time Graph for JEE

Uniform Acceleration

Electric field due to uniformly charged sphere class 12 physics JEE_Main

JEE Main 2025: Derivation of Equation of Trajectory in Physics

Atomic Structure - Electrons, Protons, Neutrons and Atomic Models

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

Learn About Angle Of Deviation In Prism: JEE Main Physics 2025

Enthalpy of Combustion with Examples for JEE

Instantaneous Velocity - Formula based Examples for JEE

JEE Advanced Weightage 2025 Chapter-Wise for Physics, Maths and Chemistry

Important Derivations for CBSE Class 12 Physics (Stepwise Solutions & PDF)




