
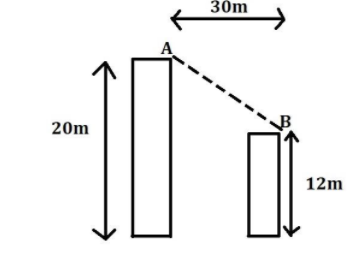
A boy wants to throw a ball from a point \[A\] so as to just clear the cliff at \[B\]. The minimum horizontal velocity with which the body should throw the ball is $(g = 10\;{\text{m}}/{{\text{s}}^2})$
(A) \[2.4m/s\]
(B) \[23.8m/s\]
(C) \[238m/s\]
(D) \[47.4m/s\]
Answer
154.5k+ views
Hint: Let us suppose a ball is thrown downwards from the edge of a cliff at an initial velocity \[u\] \[m/s\]. We know that the ball would be under the effect of gravity and would be having a positive acceleration. To find out the velocity with which the boy should throw the ball, we have to apply the equation of kinematics.
Formula Used: We will be using the following formula,
\[u = \dfrac{S}{{\sqrt {\dfrac{{2({h_1} - {h_2})}}{g}} }}\]
Where
\[u\] is the required velocity
\[S\] is the distance between the cliffs
\[{h_1}\] is the height of the taller cliff
\[{h_2}\] is the height of the shorter cliff
\[g\] is the acceleration due to gravity
Complete Step-by-Step Solution:
According to the question, the following information is provided to us:
The height of the taller cliff, \[{h_1} = 20m\]
The height of the shorter cliff, \[{h_2} = 12m/s\]
The distance between the cliffs, \[S = 30m\]
And the acceleration due to gravity, \[g = 10m/{s^2}\]
Now we will put all these values provided to us in the above formula to find out the required velocity
So, we get
\[u = \dfrac{S}{{\sqrt {\dfrac{{2({h_1} - {h_2})}}{g}} }}\]
\[ \Rightarrow u = \dfrac{{30}}{{\sqrt {\dfrac{{2(20 - 12)}}{{10}}} }}\]
Upon further solving, we get
\[\therefore u = 23.80m/s\]
Hence, the correct option is (B.)
Note: Kinematic equations are a set of four equations that can be used, if other information is known, to predict unknown information about the motion of an object. For any motion that can be described as being either a constant velocity motion or a constant acceleration motion, the equations can be used. Over any time period during which the acceleration changes, they can never be used. Four variables are part of each of the kinematic equations. The value of the fourth variable can be calculated if the values of three of the four variables are known.
Formula Used: We will be using the following formula,
\[u = \dfrac{S}{{\sqrt {\dfrac{{2({h_1} - {h_2})}}{g}} }}\]
Where
\[u\] is the required velocity
\[S\] is the distance between the cliffs
\[{h_1}\] is the height of the taller cliff
\[{h_2}\] is the height of the shorter cliff
\[g\] is the acceleration due to gravity
Complete Step-by-Step Solution:
According to the question, the following information is provided to us:
The height of the taller cliff, \[{h_1} = 20m\]
The height of the shorter cliff, \[{h_2} = 12m/s\]
The distance between the cliffs, \[S = 30m\]
And the acceleration due to gravity, \[g = 10m/{s^2}\]
Now we will put all these values provided to us in the above formula to find out the required velocity
So, we get
\[u = \dfrac{S}{{\sqrt {\dfrac{{2({h_1} - {h_2})}}{g}} }}\]
\[ \Rightarrow u = \dfrac{{30}}{{\sqrt {\dfrac{{2(20 - 12)}}{{10}}} }}\]
Upon further solving, we get
\[\therefore u = 23.80m/s\]
Hence, the correct option is (B.)
Note: Kinematic equations are a set of four equations that can be used, if other information is known, to predict unknown information about the motion of an object. For any motion that can be described as being either a constant velocity motion or a constant acceleration motion, the equations can be used. Over any time period during which the acceleration changes, they can never be used. Four variables are part of each of the kinematic equations. The value of the fourth variable can be calculated if the values of three of the four variables are known.
Recently Updated Pages
JEE Atomic Structure and Chemical Bonding important Concepts and Tips

JEE Amino Acids and Peptides Important Concepts and Tips for Exam Preparation

JEE Electricity and Magnetism Important Concepts and Tips for Exam Preparation

Chemical Properties of Hydrogen - Important Concepts for JEE Exam Preparation

JEE Energetics Important Concepts and Tips for Exam Preparation

JEE Isolation, Preparation and Properties of Non-metals Important Concepts and Tips for Exam Preparation

Trending doubts
If the unit of power is 1Kilo Watt the length is 100m class 11 physics JEE_Main

Which of the following statements is correct if the class 11 physics JEE_Main

The quantity of heat required to heat one mole of a class 11 physics JEE_Main

IIIT JEE Main Cutoff 2024

Photoelectric Effect and Stopping Potential with Work Function and Derivation for JEE

Newton’s Laws of Motion: Three Laws of Motion Explanation with Examples

Other Pages
JEE Advanced 2025 Revision Notes for Mechanics

Ideal and Non-Ideal Solutions Raoult's Law - JEE

JEE Main 2025: Conversion of Galvanometer Into Ammeter And Voltmeter in Physics

A boy wants to throw a ball from a point A so as to class 11 physics JEE_Main

List of Fastest Century In IPL - Cricket League and FAQs

NEET 2025: All Major Changes in Application Process, Pattern and More




