




How to Apply Motion Formulas to Solve Real Physics Problems
Have you ever wondered how a golf player estimates the height, speed, and trajectory of his perfect shot? All these questions can be easily understood by the concepts of motion, specifically, the kinematic equations of motion.
As per Physics, motion formulas are those equations or mathematical expressions that best describe the state of a system in motion concerning time. They are described in terms of initial velocity, acceleration, distance, displacement of the body, and time taken to complete the whole motion in any dimension, which means motion formulas can be worked on any system placed in either one, two, or even three-dimension.

Different Types of Motion
Basic Terminologies
Displacement - It is the shortest length covered by an object from a fixed point in a particular direction.
Distance - It is the total length covered by a path in a journey between two points.
Speed - It is defined as the total distance travelled per unit of time.
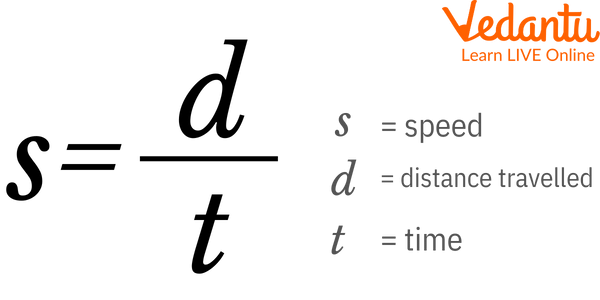
Formula for Speed
Velocity Displacement Formula
Velocity - It is defined as the rate of change of displacement per unit time of an object.
The velocity-displacement formula is given in the following image:

Equation of Velocity
Displacement Formula
By the above formula for velocity, we can also derive the displacement formula.
Wherein displacement = velocity x time interval.
Acceleration Velocity Formula
Acceleration - It is the rate of change of velocity of an object over a period of time.

Equation of Acceleration
The Kinematics Equations of Motion
Equations of motion are a set of four formulas that are used to describe the state of an object moving under constant acceleration.
These equations relate to each other by five variables
S= speed
U= initial velocity
V= final velocity
a= acceleration
t= time interval
The equations are as follows :
The First Equation of Motion
It is the relation between initial velocity, final velocity, acceleration, and time interval.

First Equation
Second Equation of Motion
It is the relation between displacement, initial velocity, acceleration, and time interval.
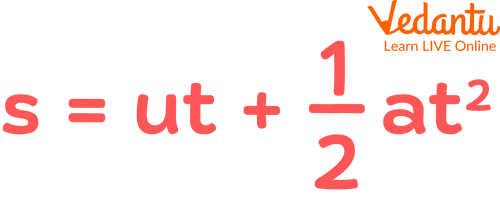
Second Equation
Third Equation of Motion
It is the relation between displacement, initial velocity, final velocity and time interval.
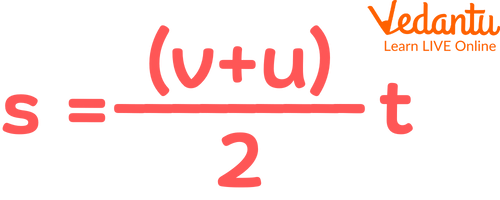
Third Equation
Squared Velocity Formula
It is the relation between acceleration, displacement, and squared initial and final velocities.
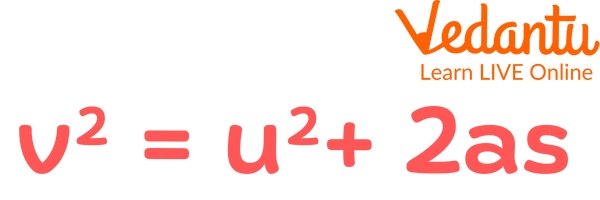
Squared Velocity Formula
Summary
For any motion under uniform acceleration, moving with a uniform initial velocity (u) to a final velocity (v), the above equations of motions can be easily applied. Equations of motion are very handy in Physics and allow us to find a solution to very sophisticated problems. All the equations of motion are explained in detail here. The equation of motion explains the behaviour of the physical system. It is explained in terms of its motion as a function of time.
FAQs on Motion Formulas Explained for Students
1. What are the three fundamental equations of motion for an object moving with uniform acceleration?
The three fundamental equations of motion, also known as kinematic equations for constant acceleration, are central to describing the motion of an object. For the CBSE 2025-26 syllabus, they are:
First Equation of Motion (Velocity-Time Relation): v = u + at
Second Equation of Motion (Position-Time Relation): s = ut + ½at²
Third Equation of Motion (Position-Velocity Relation): v² = u² + 2as
Here, u is the initial velocity, v is the final velocity, a is the constant acceleration, t is the time interval, and s is the displacement of the object.
2. What is the significance of the equations of motion in physics?
The equations of motion are fundamentally important because they provide a quantitative framework to describe and predict the state of a moving body. They allow us to calculate key variables like an object's position, velocity, or acceleration at any given point in time, provided the acceleration is constant. These formulas are the bedrock of kinematics and are essential for solving a vast range of problems, from simple projectile motion to more complex dynamics in advanced physics.
3. How does displacement differ from distance, and why is this distinction crucial when applying motion formulas?
This distinction is critical and a common point of error for students. Here's the difference:
Distance is a scalar quantity that measures the total path length covered by an object. For example, if you walk 5 metres east and then 5 metres west, your distance travelled is 10 metres.
Displacement is a vector quantity representing the shortest straight-line path between the initial and final points. In the same example, since you end up where you started, your displacement is zero.
It is crucial because the variable 's' in all three equations of motion refers specifically to displacement, not distance. Using the total distance travelled instead of displacement will lead to incorrect results, especially in scenarios where the object changes its direction of motion.
4. Under what specific conditions can the standard equations of motion be applied?
The standard equations of motion (v = u + at, etc.) are powerful but not universally applicable. Their use is valid only under two strict conditions:
The object must be moving along a straight-line path (rectilinear motion).
The acceleration ('a') of the object must be constant and uniform throughout the motion. This means the velocity must change at a steady rate.
If acceleration is variable or the path is curved, these equations cannot be used, and more advanced methods involving calculus are required.
5. How are the motion formulas adapted for an object moving under gravity?
For an object moving freely near the Earth's surface (e.g., a ball thrown upwards or dropped), the motion is governed by gravity. In this special case, the constant acceleration 'a' is replaced by the acceleration due to gravity, denoted by 'g' (approximately 9.8 m/s²). The equations become:
v = u + gt
h = ut + ½gt² (where 'h' is used for vertical height)
v² = u² + 2gh
It's important to use a consistent sign convention. For example, if upward motion is taken as positive, then 'g' (which acts downwards) must be taken as negative (-9.8 m/s²).
6. What does 'constant acceleration' precisely mean, and can you provide a real-world example?
Constant acceleration means that an object's velocity changes by an equal amount in every equal interval of time. For example, if a car's velocity increases from 0 m/s to 2 m/s in the first second, then to 4 m/s in the second second, and to 6 m/s in the third second, it has a constant acceleration of 2 m/s². The most common real-world example is an object in free fall. Neglecting air resistance, a dropped apple accelerates downwards at a constant rate of approximately 9.8 m/s², meaning its speed increases by 9.8 m/s every second.
7. Can the standard kinematic formulas be used to describe circular motion? Explain why or why not.
No, the standard kinematic formulas (v = u + at, etc.) cannot be used for circular motion, even if the object's speed is constant. This is because acceleration is a vector. In circular motion, the direction of the velocity vector is continuously changing as the object moves along the curve. This change in direction means there is always an acceleration (centripetal acceleration) directed towards the centre of the circle. Since the direction of acceleration is not constant, the condition of 'constant acceleration' is not met, making these formulas invalid. Circular motion requires its own set of descriptive equations.
8. What are the common methods used to derive the equations of motion as per the CBSE syllabus?
As per the CBSE curriculum, there are two primary methods for deriving the three equations of motion:
Graphical Method: This method is typically taught in Class 9. It involves using a velocity-time graph for an object in uniform acceleration. The acceleration is found from the slope of the graph, and the displacement is calculated from the area under the graph. Each equation can be derived visually from these properties.
Calculus Method: This method is introduced in Class 11. It uses the fundamental definitions of velocity (v = ds/dt) and acceleration (a = dv/dt). By integrating these differential equations within appropriate limits (from initial to final states), the three kinematic formulas can be derived mathematically.









