Patterns in Mathematics Class 6 Extra Questions and Answers Free PDF Download
Are you ready to make Maths super fun and easy? We’ve got a special set of important questions for CBSE Class 6 Maths Chapter 1 Patterns in Mathematics for you! These questions will help you understand the concept better.
Table of Content
Math needs more practice, so we also have extra questions to challenge you and improve your Math skills. Vedantu’s Class 6 Maths Important Questions helps students solve test papers and score well.
1. What is a pattern? Explain with an example.
Ans: A pattern is a sequence of numbers, shapes, or objects arranged in a way that follows a specific rule or order. These rules can involve addition, subtraction, multiplication, or even a geometric change.
Example: In the pattern 2, 4, 6, 8, 10, each number increases by 2, following a rule where 2 is added to the previous number each time.
2. Find the next three terms in the sequence: 2, 7, 12, 17, __, __, __.
Ans: The pattern increases by 5 each time. Adding 5 to 17 gives 22, adding 5 to 22 gives 27, and adding 5 to 27 gives 32. So, the next three terms are 22, 27, and 32.
3. Find the missing number in the pattern: 8, 16, __, 64, 128.
Ans: The pattern doubles each time. Doubling 16 gives 32, so the missing number is 32.
4. Why are 1, 3, 6, 10, 15, ... called triangular numbers?
Ans: These are called triangular numbers because the dots in these numbers can be arranged to form an equilateral triangle. For example, 6 dots can be arranged in a triangle with 3 dots at the base, 2 in the middle, and 1 at the top.
5. What do you call this sequence of numbers 1, 6, 12, 18, 24?
Ans: This sequence is an arithmetic progression where each number increases by 6. The next number will be 30.
6. Identify the rule in the pattern: 1, 8, 27, 64, __, __.
Ans: This is a pattern of cube numbers, where each number is the cube of a natural number. The next terms are 125 ($5^{3}$) and 216 ($6^{3}$).
7. Why are 1, 4, 9, 16, 25, … called square numbers or squares?
Ans: These numbers are called square numbers because they represent the area of a square. For example, 4 is the area of a square with sides of length 2 (2 $\times$ 2 = 4). Each number in this sequence is the product of a number multiplied by itself, which forms the area of a square.
8. Why are 1, 8, 27, 64, 125, … called cubes?
Ans: These numbers are called cubes because they represent the volume of a cube. For example, 8 is the volume of a cube with each side of length 2 (2 $\times$ 2 $\times$ 2 = 8). Each number in the sequence is the result of multiplying a number by itself twice, which gives the volume of a cube.
9. Look at the figure below and determine the missing piece.
Pattern:
Ans: Observe the given figure, where each section's design is formed by rotating the previous design by 90 degrees in a clockwise direction.
Therefore, the missing piece is option___.
Thus, the completed figure is:
10. Write the next three numbers in the following sequence.
198, 185, 172, 159, 146
Ans: 198, 185, 172, 159, 146
The pattern in the given sequence is:
198 – 13 = 185
185 – 13 = 172
172 – 13 = 159
159 – 13 = 146
So, the next three numbers can be written as:
146 – 13 = 133
133 – 13 = 120
120 – 13 = 107
Thus, the sequence is 198, 185, 172, 159, 146, 133, 120, 107.
11. What is the formula for the pattern of this sequence?
7, 14, 21, 28, 35, 42, 49
Ans: Given, 7, 14, 21, 28, 35, 42, 49
The numbers in this sequence are written as:
7 + 7 = 14, 14 + 7 = 21, 21 + 7 = 28, and so on.
This can also be expressed as:
7 = 7 × 1
14 = 7 × 2
21 = 7 × 3
28 = 7 × 4, and so on.
From this, we can write the formula for the above pattern as: 7n, where n = 1, 2, 3, etc.
12. Observe the pattern below and find the missing number.
Pattern:
Ans: In the given figure, we can see that the sum of the four surrounding numbers equals the number in the centre of the shape.
For example:
11 + 22 + 33 + 44 = 110
16 + 24 + 32 + 40 = 112
? + 23 + 34 + 12 = 114
To find the missing number:
? = 114 - 23 - 34 - 12 = 45
Thus, the missing number is 45.
13. Predict the next number in the following sequence.
3, 5, 10, 18, 31, ?
Ans: Given: 3, 5, 10, 18, 31, ?
Let’s calculate the difference between consecutive numbers:
5 - 3 = 2
10 - 5 = 5
18 - 10 = 8
31 - 18 = 13
The differences from the sequence: 2, 5, 8, 13
Notice that each difference increases by an increasing pattern: +3, +3, +5, ...
Thus, the next difference will be 13 + 5 = 18.
To find the next number:
31 + 18 = 49
Therefore, the next number in the sequence is 49.
14. What is the next number in the following sequence?
15, 13, 19, 10, 23, 7, 29, 3, 31, -2, 37, ?
Ans: The given sequence is:
15, 13, 19, 10, 23, 7, 29, 3, 31, -2, 37
To identify the pattern, let's calculate the differences between consecutive numbers:
13 - 15 = -2
19 - 13 = 6
10 - 19 = -9
23 - 10 = 13
7 - 23 = -16
29 - 7 = 22
3 - 29 = -26
31 - 3 = 28
-2 - 31 = -33
37 - (-2) = 39
Here, the differences follow an alternating pattern of negative and positive values, with increasing differences each time.
So, the next number in the sequence will be: 37 + 45 = 82
Thus, the next number in the sequence is 82.
15. Identify the pattern for the following sequence and find the next number.
3, 6, 10, 15, 21, 28, ____.
Ans: Given, 3, 6, 10, 15, 21, 28, ____
The pattern involved in the given sequence is:
3 + 3 = 6
6 + 4 = 10
10 + 5 = 15
15 + 6 = 21
21 + 7 = 28
28 + 8 = 36
Therefore, the next number of the given sequence is 36.
Extra Questions For Extra Marks
1. Count the number of sides in each shape in the sequence of Regular Polygons. Which number sequence do you get? What about the number of corners in each shape in the sequence of Regular Polygons? Do you get the same number sequence? Can you explain why this happens?
Ans:
Both sequences are the same because, in a regular polygon, the number of sides equals the number of vertices.
2. What happens when you multiply the triangular numbers by 6 and add 1? Which sequence do you get? Can you explain it with a picture?
Ans: Triangular numbers follow the sequence: 1, 3, 6, 10, 15, 21, etc. When you multiply each triangular number by 6 and add 1, you get a new sequence:
1×6+1=7
3×6+1=19
(increase of 12)
6×6+1=37
(increase of 18)
10×6+1=61
(increase of 24)
15×6+1=91
(increase of 30)
Thus, the sequence becomes 7, 19, 37, 61, 91, and so on. This pattern shows that each term increases by 6 more than the previous increase.
3. What would you call the following sequence of numbers?
That’s right, they are called hexagonal numbers! Draw these in your notebook. What is the next number in the sequence?
Ans: Let's break down the pattern in this sequence:
1st number = 1
2nd number = 1 + 6 = 7 (This is found by adding 6 × 1 to the 1st number)
3rd number = 7 + 12 = 19 (This is found by adding 6 × 2 to the 2nd number)
4th number = 19 + 18 = 37 (This is found by adding 6 × 3 to the 3rd number)
5th number = 37 + 24 = 61 (This is found by adding 6 × 4 to the 4th number)
Thus, the pattern involves adding multiples of 6, with each multiple increasing by 6. So, to find the next number in the sequence, you would add 6 × 5 = 30 to the 5th number (61). Therefore, the next number in the sequence would be 61 + 30 = 91.
This sequence demonstrates a regular pattern of growth, with each term increasing by a progressively larger multiple of 6.
4. Why are 1, 4, 9, 16, 25, … called square numbers or squares?
Ans: 1, 4, 9, 16, 25, … called square numbers or squares: These numbers are called square numbers because they represent the area of a square. For example, 4 is the area of a square with sides of length 2 (2 × 2 = 4). Each number in this sequence is the product of a number multiplied by itself, which forms the area of a square.
5. What would you call the following sequence of numbers?
That’s right, they are called hexagonal numbers! Draw these in your notebook. What is the next number in the sequence?
Ans: Let's break down the pattern in this sequence:
1st number = 1
2nd number = 1 + 6 = 7 (This is found by adding 6 × 1 to the 1st number)
3rd number = 7 + 12 = 19 (This is found by adding 6 × 2 to the 2nd number)
4th number = 19 + 18 = 37 (This is found by adding 6 × 3 to the 3rd number)
5th number = 37 + 24 = 61 (This is found by adding 6 × 4 to the 4th number)
Thus, the pattern involves adding multiples of 6, with each multiple increasing by 6. So, to find the next number in the sequence, you would add 6 × 5 = 30 to the 5th number (61). Therefore, the next number in the sequence would be 61 + 30 = 91.
This sequence demonstrates a regular pattern of growth, with each term increasing by a progressively larger multiple of 6.
5 Important Formulas of Class 6 Maths Chapter 1 You Shouldn’t Miss!
This page contains all the important questions from CBSE Class 6 Maths Chapter 1 - Patterns in Mathematics that you need to practise. This set of extra questions are designed to strengthen your understanding and improve your problem-solving skills.
Additionally, you will find short question answers that will help you revise quickly and prepare effectively for your exams. By practising these questions, you can perform well in your test paper.
Related Study Materials for Class 6 Maths Chapter 1 Patterns in Mathematics
CBSE Class 6 Maths (Ganita Prakash) Chapter-wise Important Questions
CBSE Class 6 Maths Study Materials
FAQs on CBSE Important Questions for Class 6 Maths Patterns in Mathematics - 2025-26
1. What are the most important topics to focus on in Class 6 Maths Chapter 1, Patterns in Mathematics, for the 2025-26 exams?
For the 2025-26 exams, students should focus on identifying and extending number patterns (like triangular and square numbers), understanding patterns in shapes involving rotation and repetition, and using basic rules to create their own patterns. Recognising patterns in addition and multiplication is also a key area.
2. What types of questions are typically asked from the Patterns in Mathematics chapter in Class 6 exams?
You can expect a mix of questions, including:
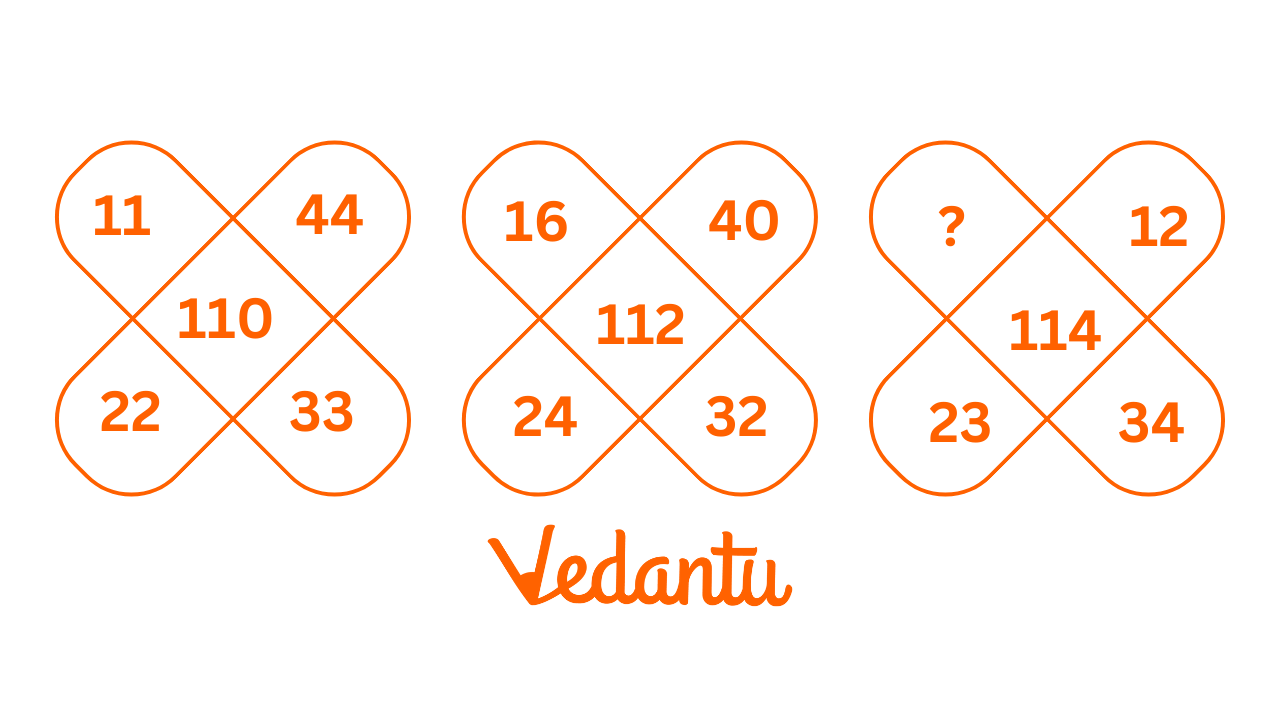
- Completing a given number or shape sequence.
- Identifying the rule that governs a pattern.
- Solving picture-based patterns.
- Questions involving patterns with odd/even numbers and multiples.
- Simple word problems where you need to identify an underlying pattern.
3. How can practising important questions for Chapter 1 help me score better in my Maths exam?
Practising a variety of important questions helps you quickly recognise different types of patterns during the exam. It improves your problem-solving speed and accuracy, and exposes you to Higher Order Thinking Skills (HOTS) questions, ensuring you are prepared for any question format as per the latest CBSE guidelines.
4. Are questions from 'Patterns in Mathematics' difficult to score in the Class 6 exam?
Generally, questions from this chapter are considered scoring and fall in the easy to moderate difficulty range. However, some HOTS questions might require you to identify a complex rule or a multi-step pattern. Consistent practice is the key to scoring full marks in this chapter.
5. Why is understanding patterns important beyond just this chapter in Class 6 Maths?
Understanding patterns is a fundamental mathematical skill. It forms the base for more advanced topics you will study later, such as algebraic expressions (where patterns are described by rules), sequences and series in higher classes, and even logical reasoning. It trains your brain to look for order and make predictions.
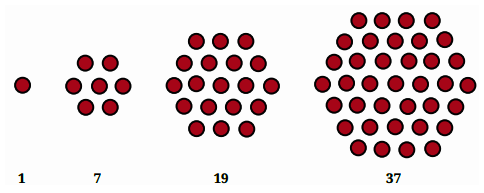
6. A question asks to find the next term in the sequence 1, 4, 9, 16, ... What is a common mistake students make?
A common mistake is to just look at the difference between consecutive terms (which is +3, +5, +7) and not recognise the underlying rule. While finding the next difference (+9) works, the core pattern is that these are square numbers (1², 2², 3², 4², ...). Recognising this fundamental rule is crucial for more complex questions and shows a deeper understanding.
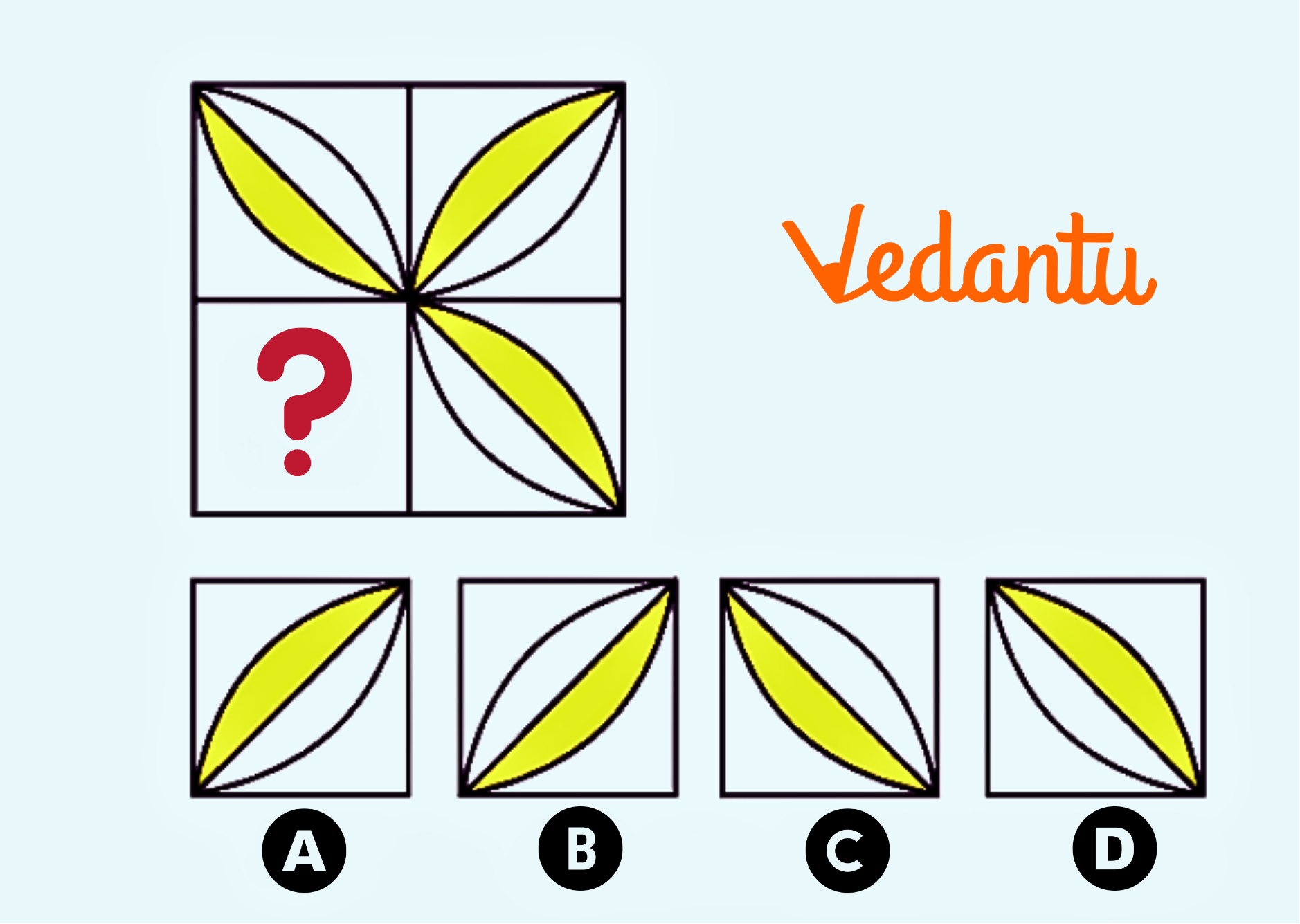
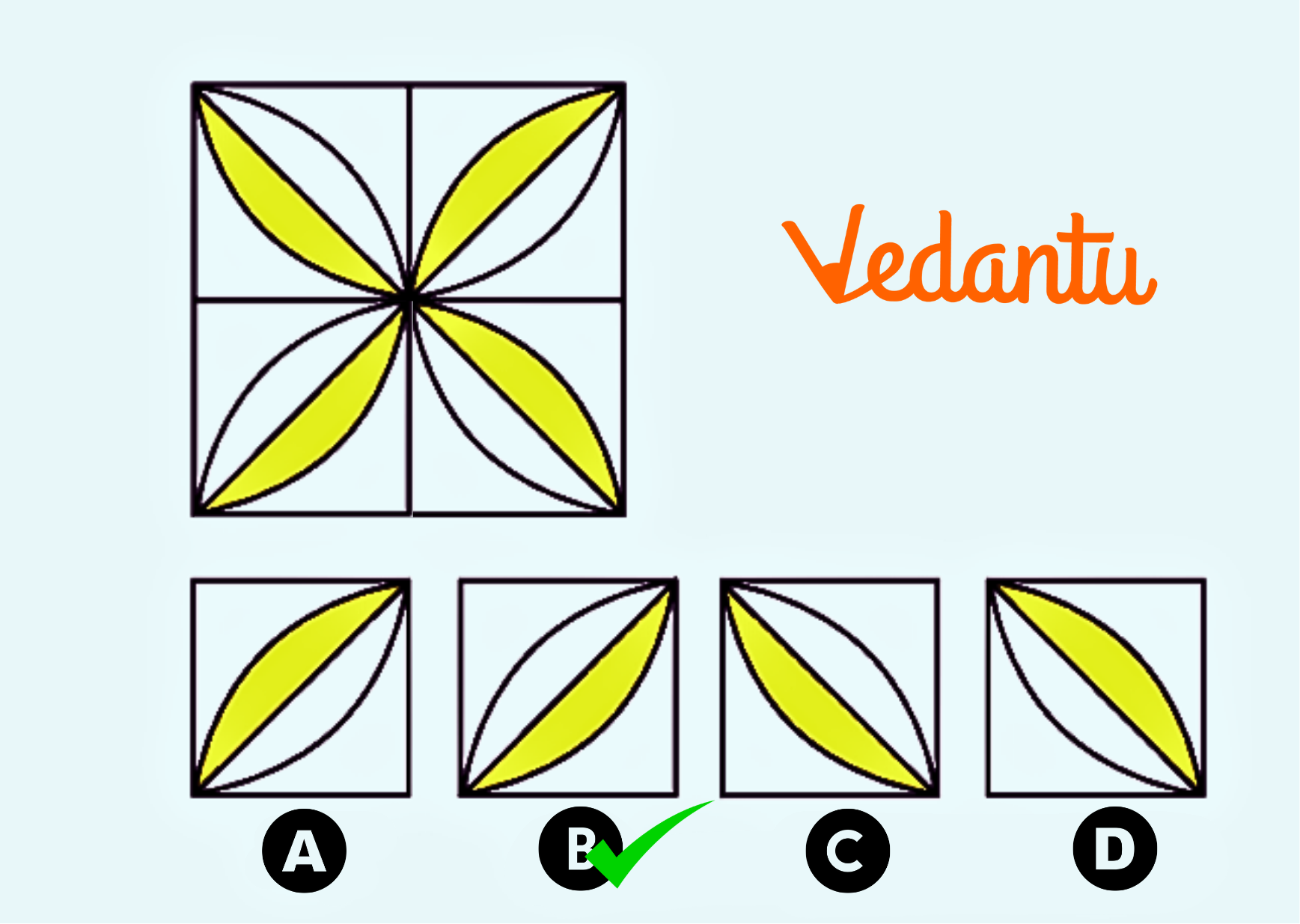
7. How should I approach a question with a complex shape-based pattern that I don't immediately recognise?
For a complex shape pattern, break it down. First, observe the change in shape or elements from one step to the next. Second, check for any rotation (clockwise or anti-clockwise) or changes in position. Third, count the number of lines, dots, or shapes in each step to see if there's a numerical pattern hidden within the visual one.
8. Can we create different patterns from the same starting numbers, like 2 and 4?
Absolutely. This is a great way to test your understanding. Starting with 2 and 4, you could create:
- An arithmetic pattern by adding 2 each time: 2, 4, 6, 8, ...
- A geometric pattern by multiplying by 2 each time: 2, 4, 8, 16, ...
- A repeating pattern: 2, 4, 2, 4, ...
