Important Questions for CBSE Class 11 Maths Chapter 11 Introduction to Three Dimensional Geometry FREE PDF Download
FAQs on CBSE Class 11 Maths Important Questions - Chapter 11 Introduction to Three Dimensional Geometry
1. What are the most common types of important questions asked from CBSE Class 11 Maths Chapter 11 Introduction to Three Dimensional Geometry in board exams?
Important question types in this chapter frequently include:
- Identifying the octant, axis, or plane in which a point lies
- Using the distance formula to prove collinearity
- Applying the section formula for given ratios (internal/external division)
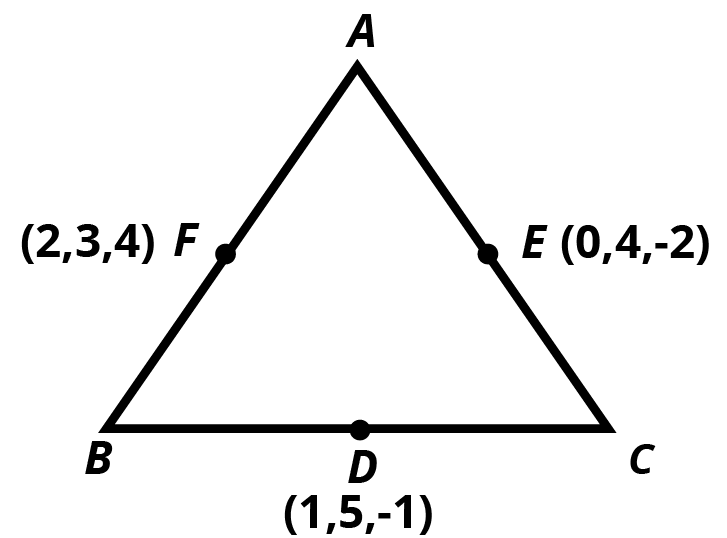
- Finding the centroid or midpoint with provided vertices or side midpoints
- Locus-based questions (determining set of points satisfying a geometric condition)
- Proofs involving tetrahedron concurrency or geometric constructions
These align with the CBSE 2025–26 exam pattern for 1, 3, 4, and 5 marks.
2. How can you quickly determine the location (octant, plane, or axis) of a point in three-dimensional geometry for MCQ or 1-mark questions?
Use the signs and zeros in the coordinates:
- All positive: First octant
- One coordinate zero: Lies on one of the coordinate planes (xy, yz, or xz)
- Two coordinates zero: On an axis (x, y, or z)
- Signs of x, y, z: Determine which octant using the (+/–) pattern
This method is tested in 1-mark CBSE objective questions.
3. How does the section formula help solve higher-order or application-based questions in Class 11 3D Geometry?
The section formula finds the coordinates of a point dividing a segment in a given ratio (internal or external). This is crucial for:
- Finding a point that divides a line between two given points
- Proving collinearity of three points (by checking if the division ratio matches for x, y, z)
- Locating centroid, trisection, and midpoints in exam scenarios
Mastery of this formula is required for 3-mark, 4-mark, and 5-mark CBSE questions as per the 2025–26 syllabus.
4. What are typical Higher Order Thinking Skills (HOTS) questions from Introduction to Three Dimensional Geometry for CBSE Class 11?
HOTS questions generally include:
- Proving concurrency of lines (such as lines from vertices of a tetrahedron to centroids of opposite faces)
- Finding the locus of points equidistant from two or more points in 3D
- Applying section formula with unconventional ratios or using planes
- Problems involving construction or proving properties of geometric figures like tetrahedrons
Such questions are commonly seen in 5-mark and 6-mark sections.
5. What is a frequent conceptual error students make when answering important questions based on 3D coordinate geometry?
A common error is confusing the coordinate planes and axes (e.g., mixing up xy-plane with yz-plane). Students also sometimes:
- Use the section formula incorrectly (especially for external division)
- Forget that all three coordinates (x, y, z) are essential in 3D (unlike in 2D problems)
- Miss squaring both sides when equating distances in locus/proof questions
Double-check the axes, coordinate values, and always include all dimensions to avoid losing marks.
6. Why is practicing important questions from Introduction to Three Dimensional Geometry crucial for both CBSE board exams and competitive tests?
Practicing important questions ensures students:
- Build a strong foundation in key 3D geometry concepts
- Gain confidence with problem types commonly tested in CBSE boards
- Develop skills necessary for reasoning and application required in JEE or other competitive exams
- Become familiar with examiner expectations for stepwise solutions and logical reasoning
7. What is the usual marking scheme and question pattern for Class 11 Introduction to Three Dimensional Geometry in the CBSE 2025–26 Maths exam?
The typical CBSE marking scheme for this chapter includes:
- 1-mark: Objective or MCQ, e.g., identify plane, axis, or octant, or give image of a point
- 3-mark: Formula application (distance, section, centroid), brief proofs, locus derivation
- 4-mark: Collinearity proofs, coordinate and section-based constructions
- 5-mark and 6-mark: HOTS, concurrency in tetrahedrons, complex loci, and construction proofs
Patterns follow the 2025–26 CBSE question blueprint, focusing on stepwise reasoning and formula usage.
8. How can you prove three points are collinear in three dimensions for an important CBSE question?
To prove collinearity:
- Calculate the distances between each pair of points (A, B, C)
- If the sum of any two side lengths equals the third (e.g., |AB| + |BC| = |AC|), then the points are collinear
- Alternatively, use the section formula and check if the ratio for x, y, and z coordinates match
Both methods are accepted per CBSE exam marking.
9. How should you approach questions asking for the locus of a point equidistant from two fixed points in 3D?
For locus questions:
- Let the coordinates of the required point be (x, y, z)
- Set up equality of distances from both given points: AP = AQ
- Square both sides, expand, and simplify to get an equation (generally of a plane in 3D)
This workflow matches CBSE 4-mark and 5-mark standards.
10. What key concepts about coordinate planes and axes are frequently tested in important questions from this chapter?
CBSE exams regularly test understanding of:
- The equations of coordinate axes (e.g., x-axis: (x, 0, 0))
- The equations of coordinate planes (e.g., xz-plane: (x, 0, z))
- The significance of zero values for determining location in 3D space
- How the signs of coordinates relate to octants
Clear identification of position is essential in 1-mark and conceptual application questions.
11. What board trends and changes are expected for important questions on Introduction to Three Dimensional Geometry in CBSE Class 11 Maths (2025–26)?
Expected trends for 2025–26 include:
- More application-based and conceptual HOTS on loci, centroids, and section formula
- Mixed-format questions combining proof and computation
- Continued emphasis on stepwise logic, with focus on distances and ratios in 3D
- Alignment of question patterns with updated sample papers and mark schemes
12. How do you use the section formula to establish collinearity of three points in 3D coordinate geometry?
To establish collinearity using the section formula:
- Assume the middle point divides the segment joining the other two in some ratio
- Set up equations using the coordinates and the ratio
- If the ratio is the same for x, y, and z, all points are collinear
This method is frequently required for 3-mark and 4-mark CBSE questions.
13. What is a common misconception in 3D geometry board questions and how can students avoid it to score full marks?
A frequent misconception is using only two coordinates when three are required, as in 2D problems. To avoid this:
- Always include x, y, and z values in all equations
- Clearly identify whether a point or its image lies on a plane or an axis
Attention to all three dimensions is vital for accuracy in CBSE board answers.
14. What strategies help secure better marks in CBSE important questions from Three Dimensional Geometry for the 2025–26 session?
Score better by:
- Learning and applying key formulas (distance, section, centroid) accurately
- Showing all steps clearly for method marks
- Practicing HOTS and expected board-level question types
- Avoiding common conceptual and calculation errors
- Studying recent CBSE sample papers to align with the latest patterns
15. How does mastering important questions from this chapter benefit students preparing for both CBSE and competitive entrance exams?
Mastery of important 3D geometry questions:
- Reinforces spatial reasoning and logical deduction
- Covers fundamental concepts required for CBSE and JEE/NEET
- Helps recognize question patterns and application methods
- Boosts overall confidence and exam performance in mathematics


















![coordinator of the centroid of triangle with vertices $A\left( {{x_1}{y_1}{z_1}} \right),{\text{B}}\left( {{x_2}{y_2}{z_2}} \right)$,T$\operatorname{and} C\left( {{x_3}{y_3}{z_3}} \right)$ is $\left[ {\dfrac{{{x_1} + {y_1} + {z_1}}}{3},\dfrac{{{y_1} + {y_2} + {y_3}}}{3},\dfrac{{{z_1} + {z_2} + {z_3}}}{3}} \right]$](https://www.vedantu.com/seo/content-images/5aaf354c-690c-4a65-a52d-1a3a90d9eb1d_1..png)