Class 11 Physics To Determine The Mass Of Two Different Objects Using A Beam Balance Experiment

A beam balance is an instrument used to calculate the weight or mass of a body subject to gravity. It is made up of a central beam held up by an agate knife resting on a support that moves inside a vertical pillar. We use beam balance in daily life to measure the weight of objects in industries and households. In this class 11 physics experiment, we'll talk about using a beam balance to compare the masses of two various objects.

Table of Content

• Aim

• Theory

• How to Make Beam Balance

• Result

Aim

To determine the mass of two different objects using a beam balance.

Apparatus Required

• Beam balance

• weight box 

• forceps 

• two objects of different masses

Theory

Beam Balance

A physical balance, also known as a beam balance, is a weighing device that uses the principle of moments to help determine an object's weight (or gravitational mass). It consists of a metal beam B with a downward-pointing knife edge in the middle. The knife's edge is supported by a firm, horizontal top (Brass). The metal beam has two edges with nuts numbered $n_1$ and $n_2$. Through stirrups, $S_1$ and $S_2$, a pair of pans $P_1$ and $P_2$ are suspended. 

To change the weights of the pan, use the nuts $n_1$ and $n_2$. A lengthy pointer P points downward in the centre of the beam. The ivory scale G on which this pointer is mounted is placed at the base of the brass pillar V. The metal beam rests on two supports, $K_1$ and $K_2$, on the pillar when it is not in use. A horizontal rod H at the bottom of the wooden box connects to a vertical pillar V. When the handle is turned to the right; the beam is elevated and ready for use. 

To make the pillar horizontal, levelling screws $W_1$ and $W_2$ are included at the bottom of the box. To support this, the pillar's side-mounted plumb line R is provided. To prevent air disturbance and to shield the balance from airborne dust particles, glass doors are supplied for the wooden box. Rotate the handle to the right after emptying the pans. The pointer P will wobble as beam B rises.

The balance is in an equilibrium state if the oscillations are symmetrical about the G centre division of the ivory scale. The instrument can be set to be in an equilibrium state by changing the nuts n1 and n2.

Beam Balance Diagram

A physical balance uses the principle of moments to calculate the gravitational mass of a body. The principle of moments states that 

Load × Load arm = Effort × Effort arm

$m_1$ g x $a_1$ = $m_2$ g x $a_2$

$m_1\,a_1 = m_2\,a_2$  

To keep the beam horizontal for a beam balance, a body with gravitational mass $m_1$ is placed in the left pan, and a standard weight of $m_2$ is placed in the right pan. If $a_1 = a_2$, then $m_1 = m_2$.

In other words, the body's gravitational mass in the left pan equals its mass in the right pan.

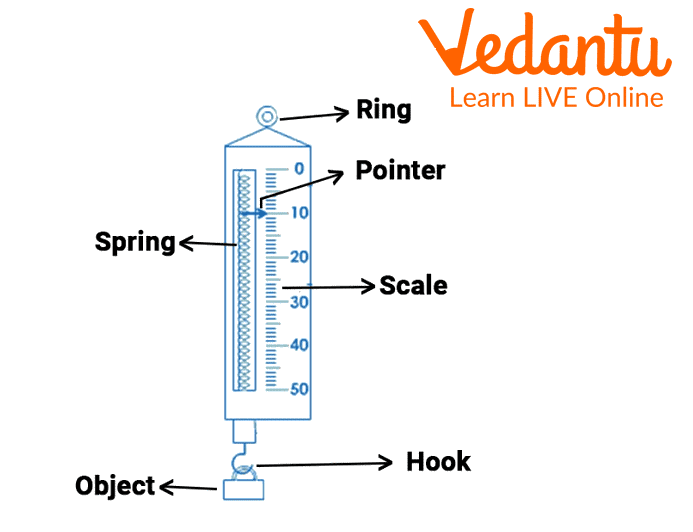
Spring Balance Diagram

How to Make Beam Balance

Material Required

• Two paper cups

• Colours/stickers

• Coat hanger

• Wire thread

Steps to Make Beam Balance

1. Start with making the beam scale buckets. Use a hole punch to create holes in two miniature paper cups.

2. Cut two pieces of twine each about one-foot long.

3. Put the ends of the twine through the cup's holes. One piece of twine should be included in each cup. When you're finished, the cups should have thin handles made of twine that resemble little bucket handles.

4. Add a notch to a coat hanger.

5. Put the buckets on the clothes hanger using the wire handles. The cups hang in the holes on the opposing ends of the clothes hangers. When you're finished, verify the buckets by lifting the scale and holding it by the top.

6. You can hang your balance scale and use the beam balance scale.

Procedure

1. The physical equilibrium should be adjusted. When the beam is extended, the pointer will remain stationary and correspond with the zero division or alternately move back and forth across the scalp about the zero division.

2. Put any object in the left pan when the beam is idle. Using the remaining forceps from the weight box, add some standard weight.

3. Close the front glass door to prevent air movement from causing a disturbance. Raise the beam with the handle, and you will notice that the beam is horizontal and that the pointer is travelling equally on both sides of the zero division. If not, use some fractional weights to shift the beam and pointer into the proper horizontal position. Bring the beam into a state of rest, gather all the weight, and add it all together to determine the gravitational mass of the thing. Now take out the item from the left pan as well.

4. Repeat the same procedure for the second object.

Observations

Table to Determine Weight.

Result

The gravitational mass of the bodies is:

(i) mass of one body, $m_1$ =………….g

(ii) mass of the other body, $m_2$ = …………g.

Precautions

1. Using forceps, carefully place the weight and the body into the pans.

2. While taking the measurement, gently close the front glass door to prevent air current from interfering with the weighing.

3. The pointer should fluctuate equally on either side of the zero mark or coincide with it.

Lab Manual Questions

1. Why is it necessary to close the shutters of the glass case for an accurate measurement?

Ans. For an accurate measurement, the glass case shutter must be closed to prevent air disturbance and the buildup of dust particles.

2. The minimum mass used from the weight box is 10 g. Find the possible instrumental error.

Ans. The least accurate measurement of mass from the weight box is 10g. Thus, the possible instrumental error will be 10g. 

3. There are two physical balances: one with equal arms and the other with unequal arms. Which one should be preferred? What additional steps do you need to take to use a physical balance with unequal arms?

Ans. The ideal physical balance will have equal arms. The mass that is to be measured by placing it in $P_1$ will then be measured again by placing it in $P_2$, and an average will be taken for both readings if the balance of the arms is unbalanced.

4. Instead of placing the mass (say a steel block) on the pan, suppose it is hanging from the same hook $S_1$ on which the pan $P_1$ is hanging (see above figure in Theory section). Will the value of the measured mass be the same or different?

Ans. If  the mass is hanging from the same hook $S_1$ on which the pan $P_1$ is hanging, then the value of the measured mass will be different.

Viva Questions

1. Define the Mass of a body.

Ans. An object's mass is the entire amount of matter it contains. It is a scalar quantity. By using beam balance, it is measured. The object's mass is constant everywhere it is. By calculating an object's inertia, we may determine its mass.

2. What is one kilogram?

Ans. The International Bureau of Weights and Measures defines it as the mass of a certain international prototype constructed of platinum-iridium and stored there. It was first specified as the mass of one litre of pure water. A mass of 1 kilogram weighs roughly 2.20 pounds at Earth's surface (lb).

3. What is the difference between mass and weight?

Ans. The primary difference between mass and weight is that a body's mass is the total amount of matter that makes up the body, whereas a body's weight is the force that is applied to it as a result of the acceleration brought on by gravity.

4. Define the gravitational mass of a body.

Ans. The gravitational force a body experiences while in the gravitational field g is what defines its gravitational mass.

5. Define the inertial mass of a body.

Ans. A body's inertial mass is its ability to resist acceleration. A force normally accelerates when it acts on a body. The inertial mass is a term used to describe a body's ability to resist acceleration caused by force.

6. How is inertial mass related to inertia?

Ans. Measurement of a body's inertia is done using its inertial mass. Inertia increases with body bulk and vice versa.

7. Define the resting point of a balance.

Ans. The place on the scale at which the pointer will come to rest when the beam stops vibrating is known as the resting point (R.R) of a balance.

8. What is the principle of working a spring balance?

Ans. It works in accordance with Hooke's law. It is based on the idea that when a body is suspended from a vertical spring, the weight of the body causes the spring's length to extend proportionately.

9. What is a true balance?

Ans. True balances are balances with equal-length arms and pans of equal weight. When the pans are empty and with equal weights on them, the beam is horizontal.

10. What is an astronomical unit of mass?

Ans. The average distance between the centres of the Earth and the Sun is measured in astronomical units (AU). Solar mass is the astronomical unit of mass. The mass of the sun, $2 \times 10^{30}$ kg, is its value.

Practical Based Questions

1. Does a body's density vary depending on where it is on Earth?

1. True

2. False

Ans. (b) False, a body's density varies with g.

 2.   What instrument is used to calculate gravitational mass?

1. Vernier Calliper

2. Screw Gauge

3. Spring Balance

Ans. (c) Spring and physical beam balance are used to determine the gravitational mass. 

3. Which of the following measures mass?

1. Voltmeter

2. Beam Balance

3. Ammeter

Ans. (b) Mass is determined using a beam balance.

4. Which among the following is a unit of mass?

1. Grams

2. Kilograms

3. tonnes

4. All of the above

Ans. (d) All of the above.

5. Mass of an object depends on

1. The temperature of the object

2. The pressure experienced by the object

3. Position of the object in space

4. None of the above

Ans. (d) None of the above. The amount of substance a thing contains determines its mass.

6. What is used to measure mass by moving weights along a beam?

1. Single beam balance

2. Double beam balance

3. Triple beam balance

Ans. (c) Triple beam balance is used to measure mass by moving weights along a beam.

7. How many types of balance are there in physics?

1. 1

2. 2

3. 3

4. 4

Ans. (c) There are three types of balance, equal arm balance, unequal arm balance, and spring balance.

8. The beam balance calibrates masses up to

1. 5 mg 

2. 5 mg to 10 mg

3. 10 mg to 20 mg

4. 10 mg to 1 kg

Ans. (d) The beam balance calibrates masses in the range of 10 mg to 1 kg. 

9. Which type of lever is beam balance?

1. Class 1 lever

2. Class 2 lever

Ans. (a) Beam balance is a type of class 1 lever.

10. What is the mass needed to shift a beam balance's resting point by one  division? 

1. Specificity 

2. Visibility 

3. Sensibility 

4. Stability

Ans. (c) Sensibility is called the mass needed to shift a beam balance's resting point by one division.

Conclusion

In this lesson, emphasis has been placed on correctly carrying out the practical experiment with the use of beam balance. However, to obtain correct values, it is crucial to implement safety precautions. Depending on the strength and sharpness of the knife edge used to make the pivot, measurements can be made with a defined resolution and accuracy.