Class 7 Maths NCERT Exemplar Solutions Chapter 2 Fractions & Decimals
Free PDF download of NCERT Exemplar for Class 7 Maths Chapter - 2 Fractions & Decimals solved by expert Maths teachers on Vedantu.com as per NCERT (CBSE) Book guidelines. All Chapter - 2 Fractions & Decimals exercise questions with solutions to help you to revise complete syllabus and score more marks in your examinations.
Access NCERT Exemplar Solutions for Class 7 Mathematics Chapter 2 - Fractions and decimals (Examples, Easy Methods and Step by Step Solutions)
Solved Examples
1. Savita is dividing ${\mathbf{1}}\dfrac{{\mathbf{3}}}{{\mathbf{4}}}\;{\mathbf{kg}}$ of sweets equally among her seven friends. How much does each friend receive?
(a) $\dfrac{{\mathbf{3}}}{{\mathbf{4}}}{\mathbf{\;kg}}$
(b) $\dfrac{{\mathbf{1}}}{{\mathbf{4}}}{\mathbf{\;kg}}$
(c) $\dfrac{{\mathbf{1}}}{{\mathbf{2}}}{\mathbf{\;kg}}$
(d) $\dfrac{{\mathbf{3}}}{{{\mathbf{28}}}}{\mathbf{\;kg}}$
Ans: Correct answer is (b)
The given number of sweets is in mixed fraction form. We will first convert it. Hence $1\dfrac{{3}}{4} = \dfrac{7}{4}$
Now according to the given condition, Savita has to divide $\dfrac{7}{4}Kg$ sweets equally among her 7 friends.
Hence, the portion of sweet one person will get ${\text{ = }}\dfrac{7}{4} \div 7 = \dfrac{1}{4}kg$
So, the amount of sweet each person will get is $\dfrac{1}{4}{\text{kg}}$.
2. If $\dfrac{{\mathbf{3}}}{{\mathbf{4}}}$ of a number is ${\mathbf{12}},$the number is
(a) ${\mathbf{9}}$
(b) ${\mathbf{16}}$
(c) ${\mathbf{18}}$
(d) ${\mathbf{32}}$
Ans: Correct answer is (b)
The number is $16$ as $\dfrac{3}{4}$ of $16 =\dfrac{3}{4} \times 16 = 12$
3. Product of fractions $\dfrac{{\mathbf{2}}}{{\mathbf{7}}}$ and $\dfrac{{\mathbf{5}}}{{\mathbf{9}}}$ is
(a) $\dfrac{{{\mathbf{2}} \times {\mathbf{5}}}}{{{\mathbf{7}} + {\mathbf{9}}}}$
(b) $\dfrac{{{\mathbf{2 + 5}}}}{{{\mathbf{2 + 9}}}}$
(c) $\dfrac{{{\mathbf{2 \times 9}}}}{{{\mathbf{5 \times 7}}}}$
(d) $\dfrac{{{\mathbf{2 \times 5}}}}{{{\mathbf{7 \times 9}}}}$
Ans: Correct answer is (d)
The product of fraction is $\dfrac{{2 \times 5}}{{7 \times 9}}$
4 Given that ${\mathbf{0 < p < q < r < s}}$ and $p,q,r,s$ are integers, which of the following is the smallest?
(a) $\dfrac{{p + q}}{{r + s}}$
(b) $\dfrac{{p + s}}{{q + r}}$
(c) $\dfrac{{q + s}}{{p + r}}$
(d) $\dfrac{{r + s}}{{p + q}}$
Ans: Correct answer is (a)
$s$ and $r$ are the largest and the second largest
$p$ and $q$ are the smallest and the second smallest
Smallest fraction $= \dfrac{{(p + q)}}{{(r + s)}}$
So, the smallest fraction from the given option is $\dfrac{{p + q}}{{r + s}}$
5. The next number of the pattern $60,30,15$, is
(a) ${\mathbf{10}}$
(b) ${\mathbf{5}}$
(c) $\dfrac{{{\mathbf{15}}}}{{\mathbf{4}}}$
(d) $\dfrac{{{\mathbf{15}}}}{{\mathbf{2}}}$
Ans: Correct answer is (d)
$\dfrac{{60}}{2} = 30$ and $\dfrac{{30}}{2} = 15$
The next number of the pattern is $\dfrac{{15}}{2}$.
6. The decimal expression for 8 rupees 8 paise (in Rupees) is
(a) ${\mathbf{8}}.{\mathbf{8}}$
(b) ${\mathbf{8}}.{\mathbf{08}}$
(c) ${\mathbf{8}}.{\mathbf{008}}$
(d) ${\mathbf{88}}.{\mathbf{0}}$
Ans: Correct answer is (b)
We know, 100paise=1 rupee
Also, 8 paise $= \dfrac{8}{{100}} = 0.08$
Thus, Decimal expansion in rupees is $(8 + 0.08) = 8.08$
7. Each side of a regular hexagon is ${\mathbf{3}}.{\mathbf{5cm}}$ long. The perimeter of the given polygon is
(a) ${\mathbf{17}}.{\mathbf{5cm}}$
(b) ${\mathbf{21\;cm}}$
(c) ${\mathbf{18}}.{\mathbf{3cm}}$
(d) ${\mathbf{20cm}}$
Ans: Correct answer is (b)
The side of a hexagon $= 3.5\;{\text{cm}}$
Total number of sides in a Hexagon $= 6$
The perimeter of hexagon $= $ sum of all six sides $= 6 \times 3.5 = 21\;{\text{cm}}$
Therefore, the perimeter of the given polygon is $21\;{\text{cm}}$.
8. ${\mathbf{2}}{\mathbf{.5 \div 1000}}$ is equal to
(a) ${\mathbf{0}}{\mathbf{.025}}$
(b) ${\mathbf{0}}{\mathbf{.0025}}$
(c) ${\mathbf{0}}{\mathbf{.2500}}$
(d) ${\mathbf{25000}}$
Ans: Correct answer is (b)
The division of $2.5 \div 1000$is $0.0025$
9. Which of the following has the smallest value?
(a) $0.0002$
(b) $\dfrac{2}{{1000}}$
(c) $\dfrac{{{{(0.2)}^2}}}{2}$
(d) $\dfrac{2}{{100}} \div 0.01$
Ans: Correct answer is (a)
The smallest value is $0.0002$ because $\dfrac{2}{{1000}}=0.002$, $\dfrac{{{{(0.2)}^2}}}{2}=\dfrac{0.04}{2}=0.02$ and $\dfrac{2}{{100}} \div 0.01=2$.
10. Which of the following has the largest value?
(a) $\dfrac{{{\mathbf{32}}}}{{{\mathbf{0}}{\mathbf{.05}}}}$
(b) $\dfrac{{{\mathbf{0}}{\mathbf{.320}}}}{{{\mathbf{50}}}}$
(c) $\dfrac{{{\mathbf{3}}{\mathbf{.2}}}}{{{\mathbf{0}}{\mathbf{.05}}}}$
(d) $\dfrac{{{\mathbf{3}}{\mathbf{.2}}}}{{{\mathbf{50}}}}$
Ans: Correct answer is (a)
The division of $\dfrac{{32}}{{0.05}} = 640$
So, the largest number is $\dfrac{{32}}{{0.05}}$
$\dfrac{{{\mathbf{0}}{\mathbf{.320}}}}{{{\mathbf{50}}}}=0.0064$
$\dfrac{{{\mathbf{3}}{\mathbf{.2}}}}{{{\mathbf{0}}{\mathbf{.05}}}}=64$
$\dfrac{{{\mathbf{3}}{\mathbf{.2}}}}{{{\mathbf{50}}}}=0.064$
11: The largest of the following is
(a) ${\mathbf{0}}{\mathbf{.0001}}$
(b) $\dfrac{{\mathbf{1}}}{{{\mathbf{1000}}}}$
(c) ${{\mathbf{(0}}{\mathbf{.100)}}^{\mathbf{2}}}$
(d) $\dfrac{{\mathbf{1}}}{{{\mathbf{10}}}}{\mathbf{ \div 0}}{\mathbf{.1}}$
Ans: Correct answer is (d).
By division $\dfrac{1}{{10}} \div 0.1 = 1$
The largest value is $\dfrac{1}{{10}} \div 0.1$
$\dfrac{{\mathbf{1}}}{{{\mathbf{1000}}}}=0.001$
${{\mathbf{(0}}{\mathbf{.100)}}^{\mathbf{2}}}=0.01$
In Examples 12 to 19, fill in the blanks to make the statement true.
12: A fraction acts as an operator_____
Ans: The given true statement is:
A fraction acts as an operator of represents multiplication
13. Fraction which is reciprocal of $\dfrac{{\mathbf{2}}}{{\mathbf{3}}}$ is_____
Ans: The given true statement is:
Fraction which is reciprocal of $\dfrac{2}{3}$ is $\dfrac{3}{2}$
14. Product of a proper and improper fraction is____ the improper fraction.
Ans: The given true statement is:
Product of a proper and improper fraction is less than the improper fraction
15. The two non-zero fractions whose product is 1, are called the____ of each other.
Ans: The given true statement is:
The two non-zero fractions whose product is 1, are called the reciprocal of each other
16: \[{\mathbf{5}}\] rupees \[{\mathbf{5}}\] paise $= Rs ?$
Ans: $1$paisa is $0.01$rupees
So $5{\text{ rupees }}5{\text{ paise }} = 5.05 $rupees
17. $45{\text{mm}} = \_\_\_{\text{m}}.$
Ans: $1{\text{ mm}} = 0.001{\text{m}}$
$45\;{\text{mm}} = 0.045{\text{m}}$
18. ${\mathbf{2}}{\mathbf{.4 \times 1000 = }}$
Ans: By multiplying $2.4 \times 1000 = 2400$
19. To divide a decimal number by ${\mathbf{100}}$, we shift the decimal point in the number to the ____by____ places.
Ans: The given true statement is :
To divide a decimal number by $100,$ we shift the decimal point in the number to the left by two places.
In Examples 20 to 23 state whether the statements are True or False.
20: Reciprocal of an improper fraction is an improper fraction.
Ans: The given statement is False
The true statement is Reciprocal of an improper fraction is a proper fraction.
21: ${\mathbf{2}}\dfrac{{\mathbf{2}}}{{\mathbf{5}}} \div {\mathbf{2}}\dfrac{{\mathbf{1}}}{{\mathbf{5}}} = {\mathbf{2}}$
Ans: The given fraction is False
The fraction of $2\dfrac{2}{5} \div 2\dfrac{1}{5} = \dfrac{{12}}{5} \times \dfrac{5}{{11}} = \dfrac{{12}}{{11}}$
22. ${\mathbf{0}}{\mathbf{.04 \div 0}}{\mathbf{.2 = 0}}{\mathbf{.2}}$
Ans: The given division is True.
${\mathbf{0}}{\mathbf{.04 \div 0}}{\mathbf{.2 = 0}}{\mathbf{.2}}$
23. ${\mathbf{0}}{\mathbf{.2 \times 0}}{\mathbf{.3 = 0}}{\mathbf{.6}}$
Ans: The given statement is False.
By multiplying the values we get $0.2 \times 0.3 = 0.06$
24. Find $\dfrac{{\mathbf{2}}}{{\mathbf{3}}}$ of \[{\mathbf{6}}\] using circles with shaded parts.

Ans: From the following figure, try to find out $\dfrac{2}{3}$ of \[6\] .
There are $12$ shaded parts out of $18$ parts which means $4$ wholes.
Thus $\dfrac{2}{3}$ of $6$ is $4$
25. Find the value of $\dfrac{{\mathbf{1}}}{{{\mathbf{4}}\dfrac{{\mathbf{2}}}{{\mathbf{7}}}}} + \dfrac{{\mathbf{1}}}{{{\mathbf{3}}\dfrac{{{\mathbf{11}}}}{{{\mathbf{13}}}}}} + \dfrac{{\mathbf{1}}}{{\left( {\dfrac{{\mathbf{5}}}{{\mathbf{9}}}} \right)}}$
Ans: ${\text{Given expression = }}$$\dfrac{1}{{\left( {\dfrac{{30}}{7}} \right)}} + \dfrac{1}{{\left( {\dfrac{{50}}{{13}}} \right)}} + \dfrac{1}{{\left( {\dfrac{5}{9}} \right)}}$
$= \dfrac{7}{{30}} + \dfrac{{13}}{{50}} + \dfrac{9}{5}$
$= \dfrac{{35}}{{150}} + \dfrac{{39}}{{150}} + \dfrac{{270}}{{150}}$
$= \dfrac{{35 + 39 + 270}}{{150}}$
$= \dfrac{{172}}{{75}}$
26. There is a ${\mathbf{3 \times 3 \times 3}}$ cube which consists of twenty seven ${\mathbf{1 \times 1 \times 1}}$ cubes (see Fig. 2.3). It is 'tunneled' by removing cubes from the coloured squares.

Find:
(i) Fraction of number of small cubes removed to the number of small cubes left in a given cube.
Ans: Number of small cubes removed $= 1 + 1 + 1 + 1 + 1 + 1 + $ $1 = 7$
So, required fraction $= \dfrac{7}{{20}}$
(ii) Fraction of the number of small cubes removed to the total number of small cubes.
Ans: The Required fraction $= \dfrac{7}{{27}}$
(iii) What part is (ii) of (i)?
Ans: Required part is $\dfrac{7}{{27}} \div \dfrac{7}{{20}} = \dfrac{7}{{27}} \times \dfrac{{20}}{7} = \dfrac{{20}}{{27}}$
27. Ramu finishes $\dfrac{{\mathbf{1}}}{{\mathbf{3}}}$ part of a work in 1 hour. How much part of the work will be finished in ${\mathbf{2}}\dfrac{{\mathbf{1}}}{{\mathbf{5}}}$ hours?
Ans: The part of the work finished by Ramu in 1 hour $= \dfrac{1}{3}$
So, the part of the work finished by Ramu in $2\dfrac{1}{5}$ hours $= 2\dfrac{1}{5} \times \dfrac{1}{3} = \dfrac{{11}}{5} \times \dfrac{1}{3}$
$= \dfrac{{11 \times 1}}{{5 \times 3}} = \dfrac{{11}}{{15}}$
Ramu will finish $\dfrac{{11}}{{15}}$ part of the work in $2\dfrac{1}{5}$ hours.
28. How many $\dfrac{{\mathbf{2}}}{{\mathbf{3}}}{\mathbf{\;kg}}$ pieces can be cut from a cake of weight ${\mathbf{4}}\;{\mathbf{kg}}$ ?
Ans: The following figure represents 4 cakes each of $1\;{\text{kg}}$ and we need pieces of $\dfrac{2}{3}$ kg.
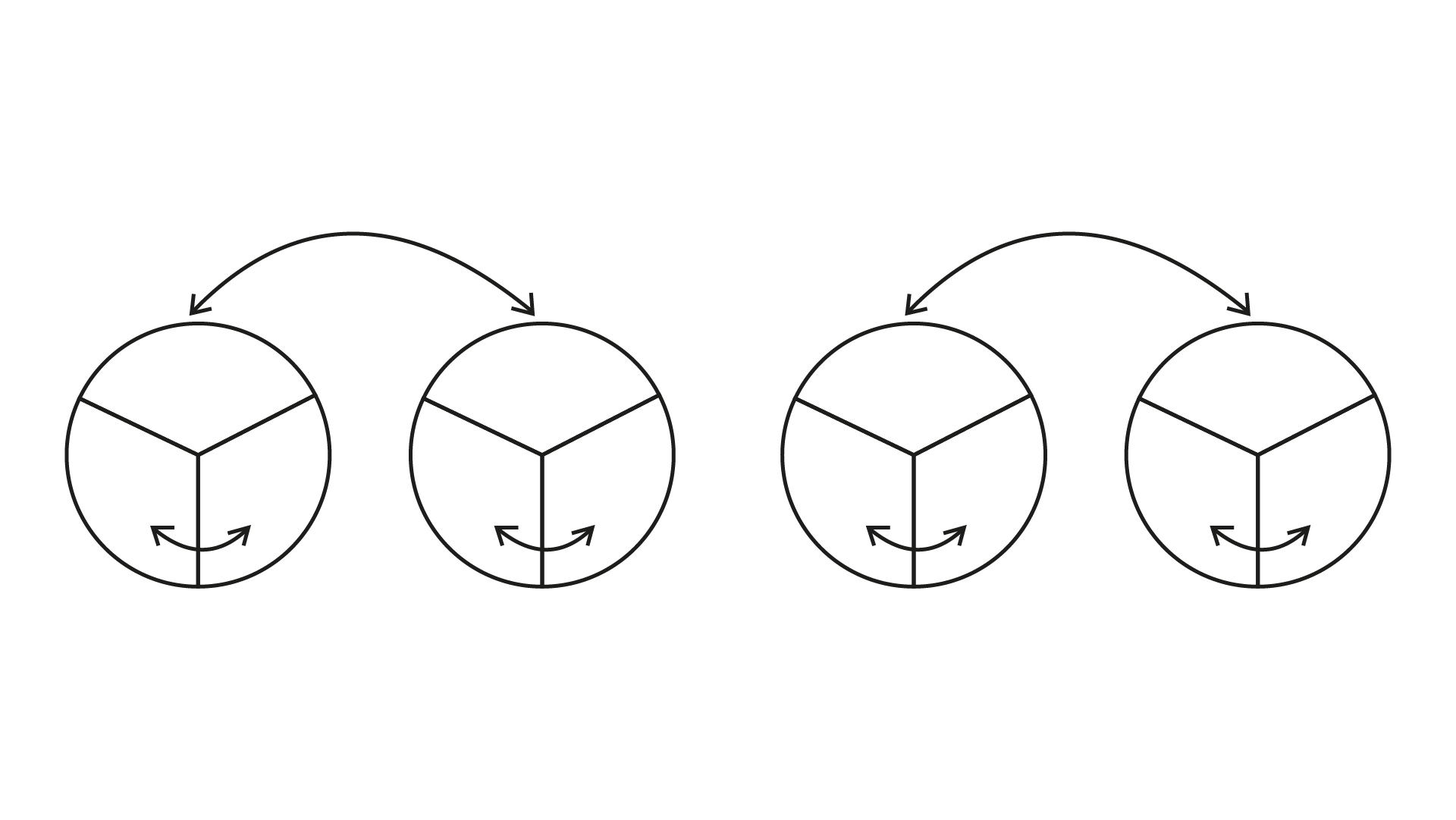
In the above figure
That is, $4 \div \dfrac{2}{3} = 4 \times \dfrac{3}{2} = 6$
29. Harmeet purchased ${\mathbf{3}}{\mathbf{.5kg}}$ of potatoes at the rate of ₹ \[{\mathbf{13}}.{\mathbf{75}}\]per kg. How much money should she pay in nearest rupees?
Ans: Cost of $1\;{\text{kg}}$ potatoes $= 13.75$.
Cost of $3.5\;{\text{kg}}$ potatoes $= 13.75 \times 3.5$
By multiplying
$13.75 \times 3.5=48.125$
Hence, cost of $3.5\;{\text{kg}}$ potatoes \[ = {\text{Rs }}48,\] to the nearest rupees.
30. Kavita had a piece of rope of length ${\mathbf{9}}{\mathbf{.5\;m}}$. She needed some small pieces of rope of length ${\mathbf{1}}{\mathbf{.9\;m}}$ each. How many pieces of the required length will she get out of this rope?
Ans: Given
The length of the rope $= 9.5\;{\text{m}}$
The length of a small piece of rope $= 1.9\;{\text{m}}$
Number of small pieces $= 9.5\;{\text{m}} \div 1.9\;{\text{m}}$
$= \dfrac{{9.5}}{{1.9}} = \dfrac{{9.5 \times 10}}{{1.9 \times 10}}$
$= \dfrac{{95}}{{19}} = 5$
So, she will get $5$ small pieces of rope.
31. Three boys earned a total of ₹\[{\mathbf{235}}.{\mathbf{50}}\]. What was the average amount earned per boy?
Ans: Three boys earned $= Rs{\mkern 1mu} 235.50$
The average amount earned per boy $= Rs\,{\kern 1pt} \dfrac{{235.50}}{3}$
By division
The average amount earned per boy is ₹\[78.50\]
32. Find the product of
(i) $\dfrac{{\mathbf{1}}}{{\mathbf{2}}}$ and $\dfrac{{\mathbf{5}}}{{\mathbf{8}}}$
Ans: The product of $\dfrac{1}{2} \times \dfrac{5}{8} = \dfrac{{1 \times 5}}{{2 \times 8}} = \dfrac{5}{{16}}$
(ii) $\dfrac{{\mathbf{1}}}{{\mathbf{3}}}$ and $\dfrac{{\mathbf{7}}}{{\mathbf{5}}}$
Ans: The product of $\dfrac{1}{3} \times \dfrac{7}{5} = \dfrac{{1 \times 7}}{{3 \times 5}} = \dfrac{7}{{15}}$
(iii) $\dfrac{{\mathbf{4}}}{{\mathbf{3}}}$ and $\dfrac{{\mathbf{5}}}{{\mathbf{2}}}$
Ans: The product of $\dfrac{4}{3} \times \dfrac{5}{2} = \dfrac{{4 \times 5}}{{3 \times 2}} = \dfrac{{20}}{6} = \dfrac{{10}}{3}$
33. Observe the 3 products given in Example 32 and now give the answers of the following questions.
(i) Does interchanging the fractions in the example, $\dfrac{{\mathbf{1}}}{{\mathbf{2}}}{\mathbf{ \times }}\dfrac{{\mathbf{5}}}{{\mathbf{8}}}$, affect the answer?
Ans: By interchanging $\dfrac{1}{2} \times \dfrac{5}{8}$ we get $\dfrac{5}{8} \times \dfrac{1}{2}$
$\dfrac{5}{8} \times \dfrac{1}{2} = \dfrac{{5 \times 1}}{{8 \times 2}} = \dfrac{5}{{16}}$ which is same as the product we get
in Example 32 by multiplying $\dfrac{1}{2}$ and $\dfrac{5}{8}$. This means that interchanging the fractions does not affect the answer.
(ii) Is the value of the fraction in the product greater or less than the value of either fraction?
Ans: By observing the 3 products given in the solution of Example 32, we come to know that the value of the fractions in the products are as follows
(a) The product of two fractions whose value is less than 1 so, the product fractions is less than each of the fractions that are multiplied.
(b) The product of a proper and an improper fraction is less than the improper fractions and greater than the proper fraction.
(c) The product of two improper fractions is greater than each of the two fractions.
34. Reshma uses $\dfrac{{\mathbf{3}}}{{\mathbf{4}}}\;{\mathbf{m}}$ of cloth to stitch a shirt. How many shirts can she make with ${\mathbf{2}}\dfrac{{\mathbf{1}}}{{\mathbf{4}}}{\mathbf{\;m}}$ cloth?
Ans: Length of cloth needed to stitch 1 shirt $= \dfrac{3}{4}\;{\text{m}}$
Length of cloth she has $= 2\dfrac{1}{4} = \dfrac{9}{4}{\text{m}}$
No. of shirts she can make by $\dfrac{9}{4}m$ cloth $= \dfrac{9}{4} \div \dfrac{3}{4}$ shirts $= \dfrac{9}{4} \times \dfrac{4}{3}$ shirts $= 3$ shirts
Hence, she can make 3 shirts using ${\mathbf{2}}\dfrac{{\mathbf{1}}}{{\mathbf{4}}}{\mathbf{\;m}}$ of cloth.
35: If the fraction of the frequencies of two notes have a common factor between the numerator and denominator, the two notes are harmonious. Use the graphic below to find the fraction of frequency of notes D and B.

Ans: Fraction of frequencies of notes ${\text{D}}$ and ${\text{B}}$ is
$= \dfrac{{{\text{ Frequency of note D}}}}{{{\text{ Frequency of note B}}}} = \dfrac{{297}}{{495}} = \dfrac{{3 \times 3 \times 3 \times 11}}{{3 \times 3 \times 5 \times 11}}$
So, the fraction of the frequencies of notes $D$ and $B$ is $\dfrac{3}{5}$.
Clearly, the notes D and B are harmonies.
36. Khilona said that we have gone about 120km or $\dfrac{2}{3}$ of the way to the campsite. So, how much farther do we have to go?
Ans: Let total distance be $x$ km.
According to question,
$\dfrac{2}{3}$ of $x=120$
$x=180$ km
Exercise
1. $\dfrac{2}{5} \times 5\dfrac{1}{5}$ is equal to:
(a) $\dfrac{{26}}{{25}}$
(b) $\dfrac{{52}}{{25}}$
(c) $\dfrac{2}{5}$
(d) \[{\mathbf{6}}\]
Ans: Option (b) is correct
Given that,
$\dfrac{2}{5} \times 5\dfrac{1}{5}$
Converting mixed fraction into the whole fraction
$\dfrac{2}{5} \times \dfrac{{26}}{5} = \dfrac{{52}}{{25}}$
2. $3\dfrac{3}{4} \div \dfrac{3}{4}$is equal to:
(a)${\mathbf{3}}$
(b) ${\mathbf{4}}$
(c) ${\mathbf{5}}$
(d) $\dfrac{{45}}{{16}}$
Ans: Option (c) is correct.
Converting mixed fraction into the whole fraction
$\dfrac{{15}}{4} \div \dfrac{3}{4}$
Converting divide into multiplication so we reciprocal the fraction $\dfrac{3}{4}$
$\dfrac{{15}}{4} \times \dfrac{4}{3} = 5$
3. A ribbon of length $5\dfrac{1}{4}\;m$ is cut into small pieces each of length $\dfrac{3}{4}\;m$. Number of pieces will be:
(a) ${\mathbf{5}}$
(b) ${\mathbf{6}}$
(c) ${\mathbf{7}}$
(d) ${\mathbf{8}}$
Ans: Option (c) is correct.
Convert the mixed fraction
The length of ribbon $= 5\dfrac{1}{4} = \dfrac{{21}}{4}m$
Length of each small piece $= \dfrac{3}{4}m$
No. of pieces $= \dfrac{{21}}{4} \div \dfrac{3}{4}$
No. of pieces $= \dfrac{{21}}{4} \times \dfrac{4}{3} = 7$
4. The ascending arrangement of $\dfrac{2}{3},\dfrac{6}{7},\dfrac{{13}}{{21}}$ is:
(a) $\dfrac{6}{7},\dfrac{2}{3},\dfrac{{13}}{{21}}$
(b) $\dfrac{{13}}{{21}},\dfrac{2}{3},\dfrac{6}{7}$
(c) $\dfrac{6}{7},\dfrac{{13}}{{21}},\dfrac{2}{3}$
(d) $\dfrac{2}{3},\dfrac{6}{7},\dfrac{{13}}{{21}}$
Ans: Option (b) is correct.
The given numbers are $\dfrac{2}{3},\dfrac{6}{7},\dfrac{{13}}{{21}}$
21 is the LCM of denominators $(3,7,21)$
$\therefore \dfrac{2}{3} = \dfrac{{2 \times 7}}{{3 \times 7}} = \dfrac{{14}}{{21}};\dfrac{6}{7} = \dfrac{{6 \times 3}}{{7 \times 3}} = \dfrac{{18}}{{21}};\dfrac{{13}}{{21}} = \dfrac{{13 \times 1}}{{21 \times 1}} = \dfrac{{13}}{{21}}$
Now $13 < 14 < 18.$
$\dfrac{{13}}{{21}} < \dfrac{{14}}{{21}} < \dfrac{{18}}{{21}} \Rightarrow \dfrac{{13}}{{21}} < \dfrac{2}{3} < \dfrac{6}{7}$
Hence, the ascending arrangement is
$\dfrac{{13}}{{21}},\dfrac{2}{3},\dfrac{6}{7}$
5. Reciprocal of the fraction $\dfrac{2}{3}$ is:
(a) ${\mathbf{2}}$
(b) ${\mathbf{3}}$
(c) $\dfrac{{\mathbf{2}}}{{\mathbf{3}}}$
(d) $\dfrac{{\mathbf{3}}}{{\mathbf{2}}}$
Ans: Option (d) is correct.
Reciprocal of the asked fraction is ${1} \div \dfrac{2}{3} = \dfrac{3}{2}$
6. The product of $\dfrac{{{\mathbf{11}}}}{{{\mathbf{13}}}}$ and \[{\mathbf{4}}\] is:
(a) ${\mathbf{3}}\dfrac{{\mathbf{5}}}{{{\mathbf{13}}}}$.
(b) ${\mathbf{5}}\dfrac{{\mathbf{3}}}{{{\mathbf{13}}}}$
(c) ${\mathbf{13}}\dfrac{{\mathbf{3}}}{{{\mathbf{5}}}}$
(d) ${\mathbf{13}}\dfrac{{\mathbf{5}}}{{{\mathbf{3}}}}$
Ans: Option (a) is correct.
The product of $\Rightarrow \dfrac{{11}}{13} \times 4 = \dfrac{{44}}{{13}}$
$= 3\dfrac{5}{{13}}$
7. The product of \[{\mathbf{3}}\] and ${\mathbf{4}}\dfrac{{\mathbf{2}}}{{\mathbf{5}}}$ is.:
(a) ${\mathbf{17}}\dfrac{{\mathbf{2}}}{{\mathbf{5}}}$
(b) $\dfrac{{{\mathbf{24}}}}{{\mathbf{5}}}$
(c) ${\mathbf{13}}\dfrac{{\mathbf{1}}}{{\mathbf{5}}}$
(d) ${\mathbf{5}}\dfrac{{\mathbf{1}}}{{{\mathbf{13}}}}$
Ans: Option (c) is correct.
First, we have to convert the mixed fraction into improper fraction $4\dfrac{2}{5} = \dfrac{{22}}{5}$
$ \Rightarrow 3 \times 4\dfrac{2}{5} = 3 \times \dfrac{{22}}{5}=\dfrac{{66}}{5}$
$= 13\dfrac{1}{5}$
8. Pictorial representation of ${\mathbf{3}} \times \dfrac{{\mathbf{2}}}{{\mathbf{3}}}$ is:
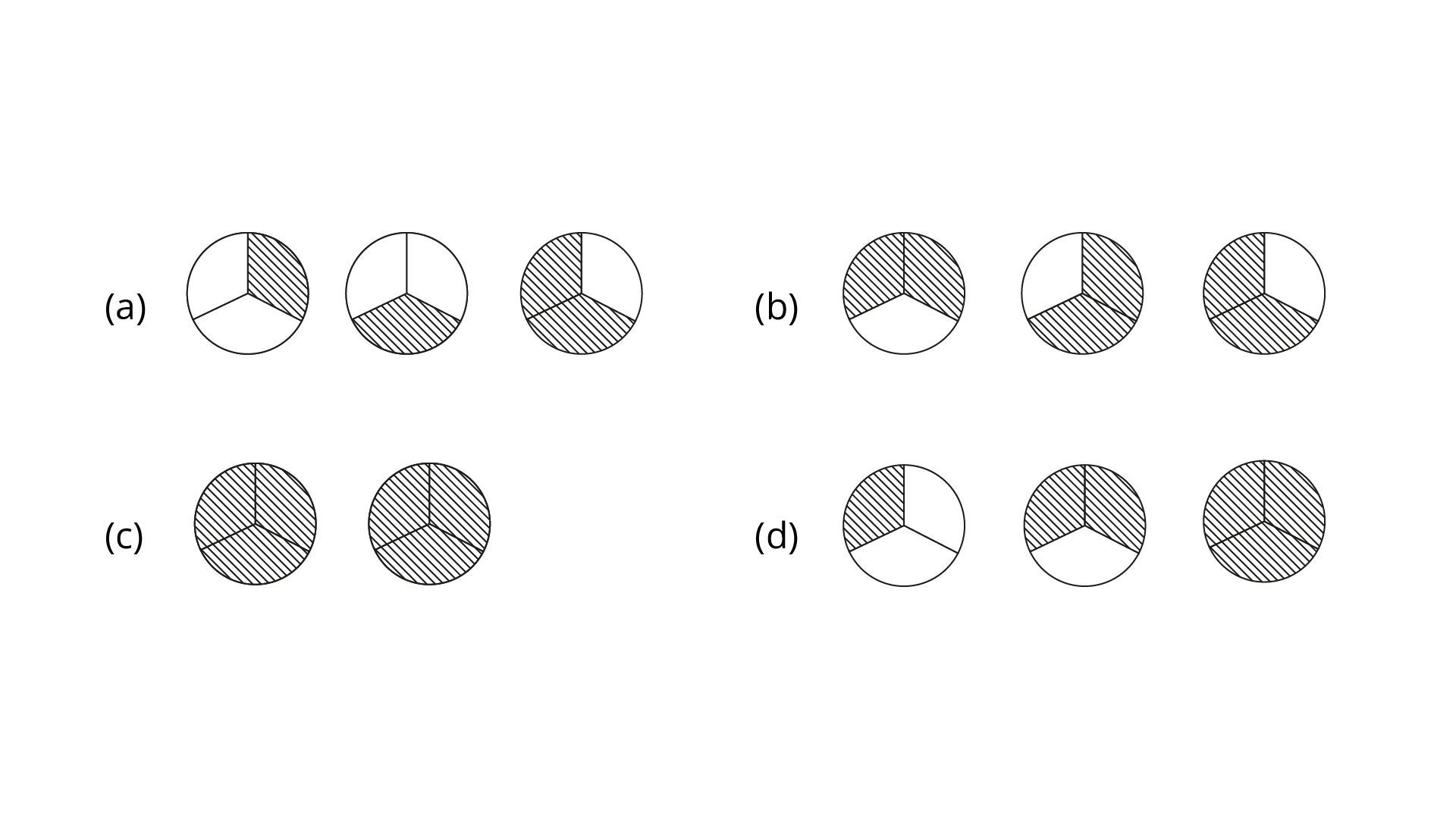
Ans: Option (b) is correct.
$3 \times \dfrac{2}{3} = \dfrac{2}{3} + \dfrac{2}{3} + \dfrac{2}{3}$
Therefore, pictorial representation is

9. $\dfrac{{\mathbf{1}}}{{\mathbf{5}}} \div \dfrac{{\mathbf{4}}}{{\mathbf{5}}}$ equal to:
(a) $\dfrac{{\mathbf{4}}}{{\mathbf{5}}}$
(b) $\dfrac{{\mathbf{1}}}{{\mathbf{5}}}$
(c) $\dfrac{{\mathbf{5}}}{{\mathbf{4}}}$
(d) $\dfrac{{\mathbf{1}}}{{\mathbf{4}}}$
Ans: Option (d) is correct.
By division $ \Rightarrow \dfrac{1}{5} \div \dfrac{4}{5} = \dfrac{1}{5} \times \dfrac{5}{4}$
$= \dfrac{1}{4}$
10. The product of ${\mathbf{0}}{\mathbf{.03 \times 0}}{\mathbf{.9}}$ is:
(a) ${\mathbf{2}}{\mathbf{.7}}$
(b) ${\mathbf{0}}{\mathbf{.27}}$
(c) ${\mathbf{0}}.{\mathbf{027}}$
(d) ${\mathbf{0}}.{\mathbf{0027}}$
Ans: Option (c) is correct.
The product of ${\mathbf{0}}{\mathbf{.03 \times 0}}{\mathbf{.9}}$
$= \dfrac{3}{{100}} \times \dfrac{{9}}{{10}}$
$= \dfrac{{27}}{{1000}} = 0.027$
11. $\dfrac{{\mathbf{5}}}{{\mathbf{7}}}{\mathbf{ \div 6}}$ is equal to:
(a) $\dfrac{{{\mathbf{30}}}}{{\mathbf{7}}}$
(b) $\dfrac{{\mathbf{5}}}{{{\mathbf{42}}}}$
(c) $\dfrac{{{\mathbf{30}}}}{{{\mathbf{42}}}}$
(d) $\dfrac{{\mathbf{6}}}{{\mathbf{7}}}$
Ans: Option (b) is correct.
By division $\dfrac{5}{7} \div 6$
$= \dfrac{5}{7} \times \dfrac{1}{6} = \dfrac{5}{{42}}$
12. ${\mathbf{5}}\dfrac{{\mathbf{1}}}{{\mathbf{6}}} \div \dfrac{{\mathbf{9}}}{{\mathbf{2}}}$ is equal to:
(a) $\dfrac{{{\mathbf{31}}}}{{\mathbf{6}}}$
(b) $\dfrac{{\mathbf{1}}}{{{\mathbf{27}}}}$
(c) ${\mathbf{5}}\dfrac{{\mathbf{1}}}{{{\mathbf{27}}}}$
(d) $\dfrac{{{\mathbf{31}}}}{{{\mathbf{27}}}}$
Ans: Option (d) is correct.
By division $5\dfrac{1}{6} \div \dfrac{9}{2}$
$= \dfrac{{31}}{6} \div \dfrac{9}{2} = \dfrac{{31}}{6} \times \dfrac{2}{9}$
$= \dfrac{{31}}{{27}}$
13. Which of the following represents $\dfrac{{\mathbf{1}}}{{\mathbf{3}}}$ of $\dfrac{{\mathbf{1}}}{{\mathbf{6}}}$ ?
(a) $\dfrac{{\mathbf{1}}}{{\mathbf{3}}} + \dfrac{{\mathbf{1}}}{{\mathbf{6}}}$
(b) $\dfrac{{\mathbf{1}}}{{\mathbf{3}}}{\mathbf{ - }}\dfrac{{\mathbf{1}}}{{\mathbf{6}}}$
(c) $\dfrac{{\mathbf{1}}}{{\mathbf{3}}}{\mathbf{ \times }}\dfrac{{\mathbf{1}}}{{\mathbf{6}}}$
(d) $\dfrac{{\mathbf{1}}}{{\mathbf{3}}}{\mathbf{ \div }}\dfrac{{\mathbf{1}}}{{\mathbf{6}}}$
Ans: Option (c) is correct.
$ \Rightarrow \dfrac{1}{3}{\text{ of }}\dfrac{1}{6} = \dfrac{1}{3} \times \dfrac{1}{6}$
14. $\dfrac{{\mathbf{3}}}{{\mathbf{7}}}$ of $\dfrac{{\mathbf{2}}}{{\mathbf{5}}}$ is equal to
(a) $\dfrac{{\mathbf{5}}}{{{\mathbf{12}}}}$
(b) $\dfrac{{\mathbf{5}}}{{{\mathbf{35}}}}$
(c) $\dfrac{{\mathbf{1}}}{{{\mathbf{35}}}}$
(d) $\dfrac{{\mathbf{6}}}{{{\mathbf{35}}}}$
Ans: Option (d) is correct.
$\dfrac{3}{7}{\text{ of }}\dfrac{2}{5} = \dfrac{3}{7} \times \dfrac{2}{5} = \dfrac{6}{{35}}$
15. One packet of biscuits requires ${\mathbf{2}}\dfrac{{\mathbf{1}}}{{\mathbf{2}}}$ cups of flour and ${\mathbf{1}}\dfrac{{\mathbf{2}}}{{\mathbf{3}}}$ cups of sugar. Estimated total quantity of both ingredients used in 10 such packets of biscuits will be
(a) less than ${\mathbf{30}}$ cups
(b) between ${\mathbf{30}}$ cups and ${\mathbf{40}}$cups
(c) between ${\mathbf{40}}$ cups and ${\mathbf{50}}$ cups
(d) above ${\mathbf{50}}$ cups
Ans: Option (c) is correct.
The requirement of sugar and flour for one packet of biscuits $= \left( {2\dfrac{1}{2} + 1\dfrac{2}{3}} \right)$
$= \left( {\dfrac{5}{2} + \dfrac{5}{3}} \right) = \left( {\dfrac{{15 + 10}}{6}} \right) = \dfrac{{25}}{6}{\text{ cups }}$
Therefore, the requirement of both ingredients for $10$ packets
$= 10 \times \dfrac{{25}}{6} = \dfrac{{125}}{3} = 41\dfrac{2}{3}{\text{ cups }}$
Total estimated quantity will lie between $40$and $50$ cups.
16. The product of ${\mathbf{7}}$ and ${\mathbf{6}}\dfrac{{\mathbf{3}}}{{\mathbf{4}}}$ is
(a) ${\mathbf{42}}\dfrac{{\mathbf{1}}}{{\mathbf{4}}}$
(b) ${\mathbf{47}}\dfrac{{\mathbf{1}}}{{\mathbf{4}}}$
(c) ${\mathbf{42}}\dfrac{{\mathbf{3}}}{{\mathbf{4}}}$
(d) ${\mathbf{47}}\dfrac{{\mathbf{3}}}{{\mathbf{4}}}$
Ans: Option (b) is correct.
The product of $7 \times 6\dfrac{3}{4}$
$= \dfrac{7}{1} \times \dfrac{{27}}{4} = \dfrac{{189}}{4}$
$= 47\dfrac{1}{4}$
17. On dividing ${\mathbf{7}}$ by $\dfrac{{\mathbf{2}}}{{\mathbf{5}}}$, the result is
(a) $\dfrac{{{\mathbf{14}}}}{{\mathbf{2}}}$
(b) $\dfrac{{{\mathbf{35}}}}{{\mathbf{4}}}$
(c) $\dfrac{{{\mathbf{14}}}}{{\mathbf{5}}}$
(d) $\dfrac{{{\mathbf{35}}}}{{\mathbf{2}}}$
Ans: Option (d) is correct.
By dividing,
$7 \div \dfrac{2}{5} = 7 \times \dfrac{5}{2} = \dfrac{{35}}{2}$
18. ${\mathbf{2}}\dfrac{{\mathbf{2}}}{{\mathbf{3}}}{\mathbf{ \div 5}}$ is equal to
(a) $\dfrac{{\mathbf{8}}}{{{\mathbf{15}}}}$
(b) $\dfrac{{{\mathbf{40}}}}{{\mathbf{3}}}$
(c) $\dfrac{{{\mathbf{40}}}}{{\mathbf{5}}}$
(d) $\dfrac{{\mathbf{8}}}{{\mathbf{3}}}$
Ans: Option (a) is correct.
First, we have to convert the mixed fraction into improper fraction $2\dfrac{2}{3} =\dfrac{8}{3}$
Then
$2\dfrac{2}{3} \div \dfrac{5}{1}$
$= \dfrac{8}{3} \times \dfrac{1}{5} = \dfrac{8}{{15}}$
19. $\dfrac{{\mathbf{4}}}{{\mathbf{5}}}$ of ${\mathbf{5\;kg}}$ apples were used on Monday. The next day $\dfrac{{\mathbf{1}}}{{\mathbf{3}}}$ of what was left was used. Weight (in ${\text{kg}}$ ) of apples left now is
(a) $\dfrac{{\mathbf{2}}}{{\mathbf{7}}}$
(b) $\dfrac{{\mathbf{1}}}{{{\mathbf{14}}}}$
(c) $\dfrac{{\mathbf{2}}}{{\mathbf{3}}}$
(d) $\dfrac{{\mathbf{4}}}{{{\mathbf{21}}}}$
Ans: Option (c) is correct.
The weight of apple used on Monday $= \dfrac{4}{5} \times 5 = 4{\text{Kg}}$
Weight of apples left on next day $= (5 - 4) = 1\;{\text{kg}}$
Weight of apples used on next day $\dfrac{1}{3}$ of $1\;{\text{kg}} = \dfrac{1}{3}$
Therefore, weight of apples left $= \left( {1 - \dfrac{1}{3}} \right) = \dfrac{2}{3}\;{\text{kg}}$
20. The picture
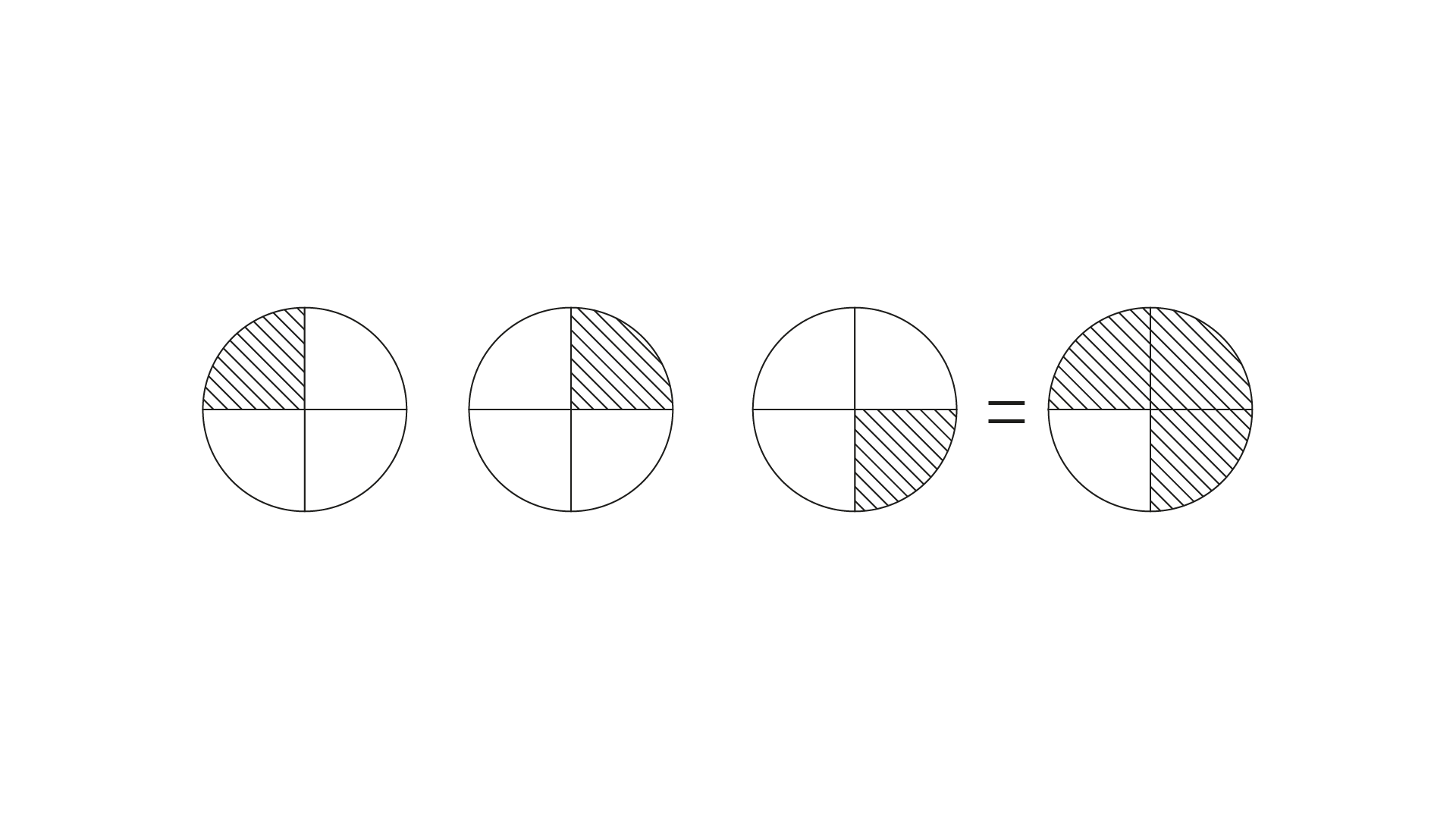
Interprets
(a) $\dfrac{{\mathbf{1}}}{{\mathbf{4}}}{\mathbf{ \div 3}}$
(b) ${\mathbf{3 \times }}\dfrac{{\mathbf{1}}}{{\mathbf{4}}}$
(c) $\dfrac{{\mathbf{3}}}{{\mathbf{4}}}{\mathbf{ \times 3}}$
(d) ${\mathbf{3 \div }}\dfrac{{\mathbf{1}}}{{\mathbf{4}}}$
Ans: Option (b) is correct.
$\dfrac{1}{4} + \dfrac{1}{4} + \dfrac{1}{4} = \dfrac{3}{4}$
In Questions 21 to 44, fill in the blanks to make the statements true.
21. Rani $\dfrac{{\mathbf{2}}}{{\mathbf{7}}}$ ate part of a cake while her brother Ravi ate $\dfrac{{\mathbf{4}}}{{\mathbf{5}}}$ of the remaining. Part of the cake left is _____
Ans: Let, there is only one cake,
Now the part of the cake ate by the Rani was $\dfrac{2}{7}$
Hence, the cake left
$ \Rightarrow 1 - \dfrac{2}{7} = \dfrac{5}{7}$
Now the part of the cake ate by the Ravi was
$ \Rightarrow \dfrac{4}{5} \times \dfrac{5}{7} = \dfrac{4}{7}$
Therefore, the cake left
$ \Rightarrow \dfrac{5}{7} - \dfrac{4}{7} = \dfrac{1}{7}$
22. The reciprocal of $\dfrac{{\mathbf{3}}}{{\mathbf{7}}}$ is______
Ans: The reciprocal of $\dfrac{3}{7}$ is \[\dfrac{7}{3}\]
23. $\dfrac{{\mathbf{2}}}{{\mathbf{3}}}$ of ${\mathbf{27}}$ is_____
Ans: The multiply of $\dfrac{2}{3} \times 27$
$= 2 \times 9 = 18$
24. $\dfrac{{\mathbf{4}}}{{\mathbf{5}}}$ of ${\mathbf{45}}$ is____
Ans: The multiply of $\dfrac{4}{5} \times 45$
$= 4 \times 9 = 36$
25. ${\mathbf{4 \times 6}}\dfrac{{\mathbf{1}}}{{\mathbf{3}}}$ is equal to______
Ans: The product of $4 \times 6\dfrac{1}{3}$
$= 4 \times \dfrac{{19}}{3} = \dfrac{{76}}{3}$
$= 25\dfrac{1}{3}$
26. $\dfrac{{\mathbf{1}}}{{\mathbf{2}}}$ of ${\mathbf{4}}\dfrac{{\mathbf{2}}}{{\mathbf{7}}}$ is_____
Ans: First we have to convert the mixed fraction into improper fraction $4\dfrac{2}{7} = \dfrac{30}{7}$
$\dfrac{1}{2}$ of $4\dfrac{2}{7}$
$= \dfrac{1}{2} \times \dfrac{{30}}{7}$
$= \dfrac{{15}}{7} = 2\dfrac{1}{7}$
27. $\dfrac{{\mathbf{1}}}{{\mathbf{9}}}$ of $\dfrac{{\mathbf{6}}}{{\mathbf{5}}}$ is________
Ans: The product the $\dfrac{1}{9}$ of $\dfrac{6}{5}$
$= \dfrac{1}{9} \times \dfrac{6}{5}$
$= \dfrac{6}{{45}} = \dfrac{2}{{15}}$
28. The lowest form of the product ${\mathbf{2}}\dfrac{{\mathbf{3}}}{{\mathbf{7}}} \times \dfrac{{\mathbf{7}}}{{\mathbf{9}}}$ is______
Ans: The lowest form of $2\dfrac{3}{7} \times \dfrac{7}{9}$
$= \dfrac{{17}}{7} \times \dfrac{7}{9}$
$= \dfrac{{17}}{9} = 1\dfrac{8}{9}$
29. $\dfrac{{\mathbf{4}}}{{\mathbf{5}}}{\mathbf{ \div 4}}$ is equal to_____
Ans: By division $\dfrac{4}{5} \div 4$
$= \dfrac{4}{5} \times \dfrac{1}{4} = \dfrac{1}{5}$
30. $\dfrac{{\mathbf{2}}}{{\mathbf{5}}}$ of $25$ is____
Ans: The product is $\dfrac{2}{5}$ of \[25\]
$= \dfrac{2}{5} \times 25$
$= 2 \times 5 = 10$
31. $\dfrac{{\mathbf{1}}}{{\mathbf{5}}} \div \dfrac{{\mathbf{5}}}{{\mathbf{6}}} = \dfrac{{\mathbf{1}}}{{\mathbf{5}}}\_\_\dfrac{{\mathbf{6}}}{{\mathbf{5}}}$
Ans: While dividing one fraction by another fraction, we multiply the first fraction by the reciprocal of the other.
$\dfrac{1}{5} \div \dfrac{5}{6} = \dfrac{1}{5} \times \dfrac{6}{5}$
32. ${\mathbf{3}}{\mathbf{.2 \times 10 = }}$
Ans: To multiply a decimal number by 10, we move the decimal point in the number to the right by as many places as many zeros $(0)$ are at the right of one
$3.2 \times 10 = 32$
33. ${\mathbf{25}}{\mathbf{.4 \times 1000 = }}$
Ans: To multiply a decimal number by \[1000\] we move the decimal point in the number to the right by as many places as many zeros $(0)$ are at the right of one.
$25.4 \times 1000 = 25400$
34. ${\mathbf{93}}{\mathbf{.5 \times 100 = }}$
Ans: To multiply a decimal number by \[100\] we move the decimal point in the number to the right by as many places as many zeros $(0)$ are at the right of one
$93.5 \times 100 = 9350$
35. ${\mathbf{4}}{\mathbf{.7 \div 10 = }}$
Ans: To divide a decimal number by \[\;10\], shift the decimal point in the decimal number to the left by as many places as there are zeros over 1, to get the quotient.
$4.7 \div 10 = 0.47$
36. ${\mathbf{4}}.{\mathbf{7}} \div {\mathbf{100}} = $
Ans: To divide a decimal number by \[100,\] shift the decimal point in the decimal number to the left by as many places as there are zeros over 1, to get the quotient.
$4.7 \div 100 = 0.047$
37. ${\mathbf{4}}.{\mathbf{7}} \div {\mathbf{1000}} = $
Ans: To divide a decimal number by \[1000\], shift the decimal point in the decimal number to
the left by as many places as there are zeros over 1, to get the quotient.
$4.7 \div 1000 = 0.0047$
38. The product of two proper fractions is______than each of the fractions that are multiplied.
Ans: The product of two proper fractions is less than each of the fractions that are multiplied.
39. While dividing a fraction by another fraction, we _________ the first fraction by the _______ of the other fraction.
Ans: While dividing a fraction by another fraction, we multiply the first fraction by the reciprocal of the other fraction.
40. $8.4 \div \_\_\_ = 2.1$
Ans: $8.4 \div \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{4} = 2.1$
Let us assume the missing fraction be $x$,
Then,
$8.4 \div x = 2.1$
$8.4/x = 2.1$
By cross multiplication, we get,
$x = 8.4/2.1$
$x = 84/21$
$x = 28/7$
$x = 4$
41. ${\mathbf{52}}{\mathbf{.7 \div }}\_\_\_\_ = {\mathbf{0}}{\mathbf{.527}}$
Ans: Let consider $x$ be the missing variable
$52.7 \div {\text{x}} = 0.527$
${\text{x}} = \dfrac{{52.7}}{{0.527}} = 100$
$x = 100$
42. ${\mathbf{0}}{\mathbf{.5\_\_\_0}}{\mathbf{.7 = 0}}{\mathbf{.35}}$
Ans: Let determine the exponent
$0.5{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{of}}{\kern 1pt} \,0.7 = 0.35$
So, $0.5 \times 0.7 = 0.35$
43. ${\mathbf{2}}\_\_\_\dfrac{{\mathbf{5}}}{{\mathbf{3}}}{\mathbf{ = }}\dfrac{{{\mathbf{10}}}}{{\mathbf{3}}}$
Ans: The missing exponent is
$\Rightarrow 2 \times \dfrac{5}{3} = \dfrac{{10}}{3}$
$= 2 \times \dfrac{5}{3} = \dfrac{{10}}{3}$
44. ${\mathbf{2}}{\mathbf{.001 \div 0}}{\mathbf{.003 = }}$
Ans: By division
$\Rightarrow 2.001 \div 0.003 =$
$= \dfrac{{2001}}{{1000}} \times \dfrac{1000}{{3}}$
$= 667$
In each of the Questions 45 to 54, state whether the statement is True or False.
45. The reciprocal of a proper fraction is a proper fraction.
Ans: The given statement is False,
So, the correct statement is the reciprocal of a proper fraction is an improper fraction.
46. The reciprocal of an improper fraction is an improper fraction.
Ans: The given statement is False,
So, the correct statement is the reciprocal of an improper fraction is a proper fraction.
47. ${\text{Product of two fractions = }}\dfrac{{{\text{ Product of their denominators }}}}{{{\text{ Product of their numerators }}}}$
Ans: The given statement is false.
The correct statement is ${\text{Product}}{\kern 1pt} \,{\kern 1pt} {\text{of}}\,\,{\text{two}}{\mkern 1mu} {\text{fractions}} = \dfrac{{{\text{ Product of their numerators }}}}{{{\text{ Product of their denominators }}}}$
48. The product of two improper fractions is less than both the fractions.
Ans: The given statement is False,
Correct statement is the product of two improper fractions is greater than both the fractions.
49. A reciprocal of a fraction is obtained by inverting it upside down.
Ans: The given statement is True
50. To multiply a decimal number by $1000$ , we move the decimal point in the number to the right by three places.
Ans: The given statement is True
51. To divide a decimal number by $100$ , we move the decimal point in the number to the left by two places.
Ans: The given statement is True
52. 1 is the only number which is its own reciprocal.
Ans: The given statement is True
53. $\dfrac{{\mathbf{2}}}{{\mathbf{3}}}$ of \[{\mathbf{8}}\] is same as $\dfrac{{\mathbf{2}}}{{\mathbf{3}}}{\mathbf{ \div 8}}$
Ans: The given statement is False
The product of $\dfrac{2}{3} \times 8 = \dfrac{{16}}{3}$
And
The division of $\dfrac{2}{3} \div 8 = \dfrac{2}{3} \times \dfrac{1}{8} = \dfrac{1}{{12}}$
$\dfrac{2}{3}{\text{ of }}8 \ne \dfrac{2}{3} \div 8$
54. The reciprocal of $\dfrac{{\mathbf{4}}}{{\mathbf{7}}}$ is $\dfrac{{\mathbf{4}}}{{\mathbf{7}}}$
Ans: The given statement is False,
The reciprocal of $\dfrac{4}{7}$ is $\dfrac{7}{4}$
55. If ${\mathbf{5}}$ is added to both the numerator and the denominator of the fraction $\dfrac{5}{9}$, will the value of the fraction be changed? If so, will the value increase or decrease?
Ans: Given, $\dfrac{5}{9}$ and $\dfrac{{5 + 5}}{{9 + 5}} = \dfrac{{10}}{{14}} = \dfrac{5}{7}$
Here, $\dfrac{5}{9} \ne \dfrac{5}{7}$
Now, $\dfrac{5}{9} < \dfrac{5}{7}$
Therefore, the value is increased.
56. What happens to the value of a fraction if the denominator of the fraction is decreased while the numerator is kept unchanged?
Ans: If the denominator of the fraction is decreased, the value of a fraction is increased while the numerator remains unchanged.
57. Which letter comes $\dfrac{{\mathbf{2}}}{{\mathbf{5}}}$ of the way among ${\text{A}}$ and\[{\mathbf{J}}\]?
Ans: The total letter in number between ${\text{A}}$ and ${\text{J}}$ is $10.$
Then, $\dfrac{2}{5} \times 10 = 4$
Therefore, D comes at $\dfrac{4}{{10}}$.
58. If $\dfrac{{\mathbf{2}}}{{\mathbf{3}}}$ of a number is \[{\mathbf{10}}\], then what is ${\mathbf{1}}{\mathbf{.75}}$ times of that number?
Ans: Let $x$ be the number
$\dfrac{2}{3} \times x = 10$
$ \Rightarrow \dfrac{2}{3} \times x = 10$
$ \Rightarrow x = 10 \div \dfrac{2}{3} = 10 \times \dfrac{3}{2}$
$ \Rightarrow x = 5 \times 3 = 15$
${\text{Now, }}1.75 \times x = 1.75 \times 15 = 26.25$
59. In a class of ${\mathbf{40}}$ students, $\dfrac{{\mathbf{1}}}{{\mathbf{5}}}$ of the total number of students like to eat rice only, $\dfrac{{\mathbf{2}}}{{\mathbf{5}}}$ of the total numbers of students like to eat chapati only and the remaining students like to eat both. What fractions of the total number of students like to eat both?
Ans: Given,
Total number of students is $40$
Number student who eats rice only $= \dfrac{1}{5} \times 40 = 8$
Number student who eats chapati only $= \dfrac{2}{5} \times 40 = 16$
Number of students who eats both $= 40 - (8 + 16) = 16$
Therefore, the required fraction $= \dfrac{{16}}{{40}} = \dfrac{2}{5}$
60. Renu completed $\dfrac{{\mathbf{2}}}{{\mathbf{3}}}$ part of her homework in \[{\mathbf{2}}\] hours. How much part of her homework had she completed in ${\mathbf{1}}\dfrac{{\mathbf{1}}}{{\mathbf{4}}}$ hours?
Ans: Let total homework denoted as $x$
Renu completed the part of homework in $2$ hours $= \dfrac{2}{3}x$
Thus, completed work by her in an hour
$= \dfrac{2}{3}x \times \dfrac{1}{2}$
$= \dfrac{x}{3}$
Therefore, the part of completed in $1\dfrac{1}{4}$ hours
$\dfrac{x}{3} \times 1\dfrac{1}{4} = \dfrac{x}{3} \times \dfrac{5}{4}$
$= \dfrac{{5x}}{{12}}$
61. Reemu read $\dfrac{{\mathbf{1}}}{{\mathbf{5}}}$ th pages of a book. If she reads further ${\mathbf{40}}$ pages, she would have read $\dfrac{{\mathbf{7}}}{{{\mathbf{10}}}}$ th pages of the book. How many pages are left to be read?
Ans: The total page inside the book be $x$ and number of pages read by Reemu $=\dfrac{x}{5} + 40 = \dfrac{7x}{{10}}$
$\dfrac{7x}{{10}} - \dfrac{x}{5} = 40$
$\left[ {\dfrac{{(7 - 2)}}{{10}}} \right]x = 40$
$\dfrac{5}{{10}}x = 40$
$x = \dfrac{{40 \times 10}}{5} = 80$
Now, number of pages read by Reemu $= \dfrac{7}{{10}} \times 80 = 56$
Therefore, number of pages remains to be read $= (80 - 56) = 24$
62. Write the number in the box $\square $ such that
$\dfrac{{\mathbf{3}}}{{\mathbf{7}}}{\mathbf{ \times }}\_\_\_{\mathbf{ = }}\dfrac{{{\mathbf{15}}}}{{{\mathbf{98}}}}$
Ans: Let number in the box be $y$
$\dfrac{3}{7} \times y = \dfrac{{15}}{{98}}$
$y = \dfrac{{15}}{{98}} \div \dfrac{3}{7}$
$y = \dfrac{{15}}{{98}} \times \dfrac{7}{3} = \dfrac{5}{{14}}$
Therefore, the required number is $\dfrac{5}{{14}}$.
63. Will be quotient ${\mathbf{7}}\dfrac{{\mathbf{1}}}{{\mathbf{6}}}{\mathbf{ \div 3}}\dfrac{{\mathbf{2}}}{{\mathbf{3}}}$ be a fraction greater than ${\mathbf{1}}{\mathbf{.5}}$ or less than\[{\mathbf{1}}.{\mathbf{5}}\]? Explain.
Ans: The quotient of
$7\dfrac{1}{6} \div 3\dfrac{2}{3} = \dfrac{{43}}{6} \div \dfrac{{11}}{3}$
$= \dfrac{{43}}{6} \times \dfrac{3}{{11}} = \dfrac{{43}}{{22}}$
$= 1.95$
Therefore, $7\dfrac{1}{6} \div 3\dfrac{2}{3}$ fraction is greater than $1.5$.
64. Describe two methods to compare $\dfrac{{{\mathbf{13}}}}{{{\mathbf{17}}}}$ and ${\mathbf{0}}{\mathbf{.82}}{\mathbf{.}}$ Which do you think is easier and why?
Ans: Method-I: Conversion of both numbers $\dfrac{{13}}{{17}}$ and \[0.82\]
$\dfrac{{13}}{{17}} = 0.76$ and $0.82$
Method-II: Change into fraction
$0.82 = \dfrac{{82}}{{100}} = \dfrac{{41}}{{50}}$ and $\dfrac{{13}}{{17}}$
Hence, the method of converting numbers into decimals is easy.
65. Health: the directions for a pain reliever recommend that an adult of ${\mathbf{60}}$ kg and over take ${\mathbf{4}}$tablets every 4 hours as needed, and an adult who weighs between ${\mathbf{40}}$ and ${\mathbf{50\;kg}}$ take only ${\mathbf{2}}\dfrac{{\mathbf{1}}}{{\mathbf{2}}}$ tablets every 4 hours as needed. Each tablet weighs $\dfrac{{\mathbf{4}}}{{{\mathbf{25}}}}$ grams.
(a) If a ${\mathbf{72\;kg}}$ adult takes 4 tablets, how many grams of pain reliever is he or she receiving?
Ans: Each tablets of $\dfrac{{\mathbf{4}}}{{{\mathbf{25}}}}$ grams
Then, weight of ${\mathbf{4}}$ tablets $= 4 \times \dfrac{4}{{25}} = \dfrac{{16}}{{25}}grams$
(b) How many grams of pain reliever is the recommended dose for an adult weighing ${\mathbf{46\;kg}}$ ?
Ans: An adult of who has weight of $46$ takes $2\dfrac{1}{2}$Tablets
Hence, weight of $2\dfrac{1}{2}$ Tablets
$\dfrac{4}{{25}} \times 2\dfrac{1}{2}$ gram
$= \dfrac{4}{{25}} \times \dfrac{5}{2} = \dfrac{2}{5}$ grams
66. Animals: The label on a bottle of pet vitamins lists dosage guidelines. What dosage would you give to each of these animals?
Do Good Pet Vitamins
• Adult dogs: $\dfrac{1}{2}$ tsp (tea spoon full) per 9kg body weight
• Puppies, pregnant dogs, or nursing dogs: $\dfrac{1}{2}$ tsp per 4.5kg body weight
• Cats: $\dfrac{1}{4}$ tsp per 1kg body weight
(a) A ${\mathbf{18\;kg}}$ adult dog
Ans: Dosage given to a $18\;{\text{kg}}$ adult dog
$= \left( {\dfrac{1}{2} + \dfrac{1}{2}} \right) = 1{\text{tsp}}$
(b) A ${\mathbf{6\;kg}}$ cat
Ans: Total dosages are given to a cat of weight \[6\] ${\text{kg}}$
$= 6 \times \dfrac{1}{4} = 1\dfrac{1}{2}{\text{tsp}}$
(c) A ${\mathbf{18\;kg}}$ pregnant dog
Ans: Dosages are given to a pregnant dog weighing $18\;{\text{kg}}$
$= \dfrac{1}{2} \times \dfrac{1}{{4.5}} \times 18$
$= 9 \times \dfrac{{10}}{{45}} = 2{\text{tsp}}$
67. How many $\dfrac{{\mathbf{1}}}{{{\mathbf{16}}}}$ kg boxes of chocolates can be made with ${\mathbf{1}}\dfrac{{\mathbf{1}}}{{\mathbf{2}}}{\mathbf{\;kg}}$ chocolates?
Ans: 1 box filled with $\dfrac{1}{{16}}\;{\text{kg}}$ of chocolates.
Hence, $1\;{\text{kg}}$ chocolates to be filled in $1 \div \dfrac{1}{{16}}$ $= 1 \times 16 = 16$ boxes
Now, $1\dfrac{1}{2}{\text{Kg}}$ chocolates to be filled
$16 \times 1\dfrac{1}{2} = 16 \times \dfrac{3}{2} = 24{\text{ boxes }}$
68. Anvi is making a bookmarker like the one shown in Fig. 2.6. How many bookmarks can she make from a ${\mathbf{15\;m}}$ long ribbon?

Ans: Length of one bookmaker $= 10\dfrac{1}{2} = \dfrac{{21}}{2}\;{\text{cm}}$
Avni can make the number of bookmaker, from the ribbon of size $15 \times 100$
$= \left( {\dfrac{1}{{21 \div 2}} \times 15 \times 100} \right) = \dfrac{2}{{21}} \times 1500$
$= \dfrac{{3000}}{{21}} = 142.8 \approx 142$
Avni can make $142$ bookmakers from a $15\;{\text{m}}$ long ribbon.
69. A rule for finding the approximate length of diagonal of a square is to multiply the length of a side of the square by ${\mathbf{1}}.{\mathbf{414}}$. Find the length of the diagonal when:
(a) The length of a side of the square is ${\mathbf{8}}{\mathbf{.3\;cm}}$.
Ans: The square side's length is $8.3\;{\text{cm}}$
Diagonal length of the square
$1.414 \times 8.3 = 11.736 \approx 11.74\;{\text{cm}}$
(b) The length of a side of the square is exactly ${\mathbf{7}}{\mathbf{.875}}{\kern 1pt} \,{\mathbf{cm}}$.
Ans: The square side's length is $7.875\;{\text{cm}}$
Diagonal length of the square
$= 1.414 \times 7.875$
$= 11.135 \approx 11.14\;{\text{cm}}$
70. The largest square that can be drawn in a circle has a side whose length is ${\mathbf{0}}{\mathbf{.707}}$times the diameter of the circle. By this rule, find the length of the side of such a square when the diameter of the circle is
(a) ${\mathbf{14}}{\mathbf{.35\;cm}}$
Ans: The Circle's diameter is $14.35\;{\text{cm}}$.
Thus, the square side's length is $= 0.707 \times 14.35$
$= 10.14545 = 10.15\;{\text{cm}}$
(b) ${\mathbf{8}}{\mathbf{.63\;cm}}$
Ans: The Circle's diameter is $8.63\;{\text{cm}}$.
Thus, the square side's length is $= 0.707 \times 8.63$
$= 6.10141 = 6.10\;{\text{cm}}$
71. To find the distance around a circular disc, multiply the diameter of the disc by ${\mathbf{3}}.{\mathbf{14}}$. What is the distance around the disc when:
(a) the diameter is ${\mathbf{18}}{\mathbf{.7\;cm}}$ ?
Ans: Diameter of the disc is $18.7\;{\text{cm}}$.
Thus, the distance around the disc $= 3.14 \times 18.7$
$= 58.718\;{\text{cm}}$
(b) the radius is ${\mathbf{6}}{\mathbf{.45\;cm}}$ ?
Ans: Disc's radius is $6.45\;{\text{cm}}$
Diameter of disc is $6.45 \times 2 = 12.9\;{\text{cm}}$
Thus, the distance around the disc is $= 3.14 \times 12.9 = 40.506\;{\text{cm}}$
72. What is the cost of ${\mathbf{27}}{\mathbf{.5\;m}}$ of cloth at ${\mathbf{53}}{\mathbf{.50}}$ per meter?
Ans: Given cost of $1$ meter of cloth is Rs $53.50$
Thus, Cost of $27.5$ meters of cloth is
$(53.50 \times 27.5) = Rs.1471.25$
73. In a hurdle race, Nidhi is over hurdle B and $\dfrac{{\mathbf{2}}}{{\mathbf{6}}}$ of the way through the race, as shown in Fig. 2.7.
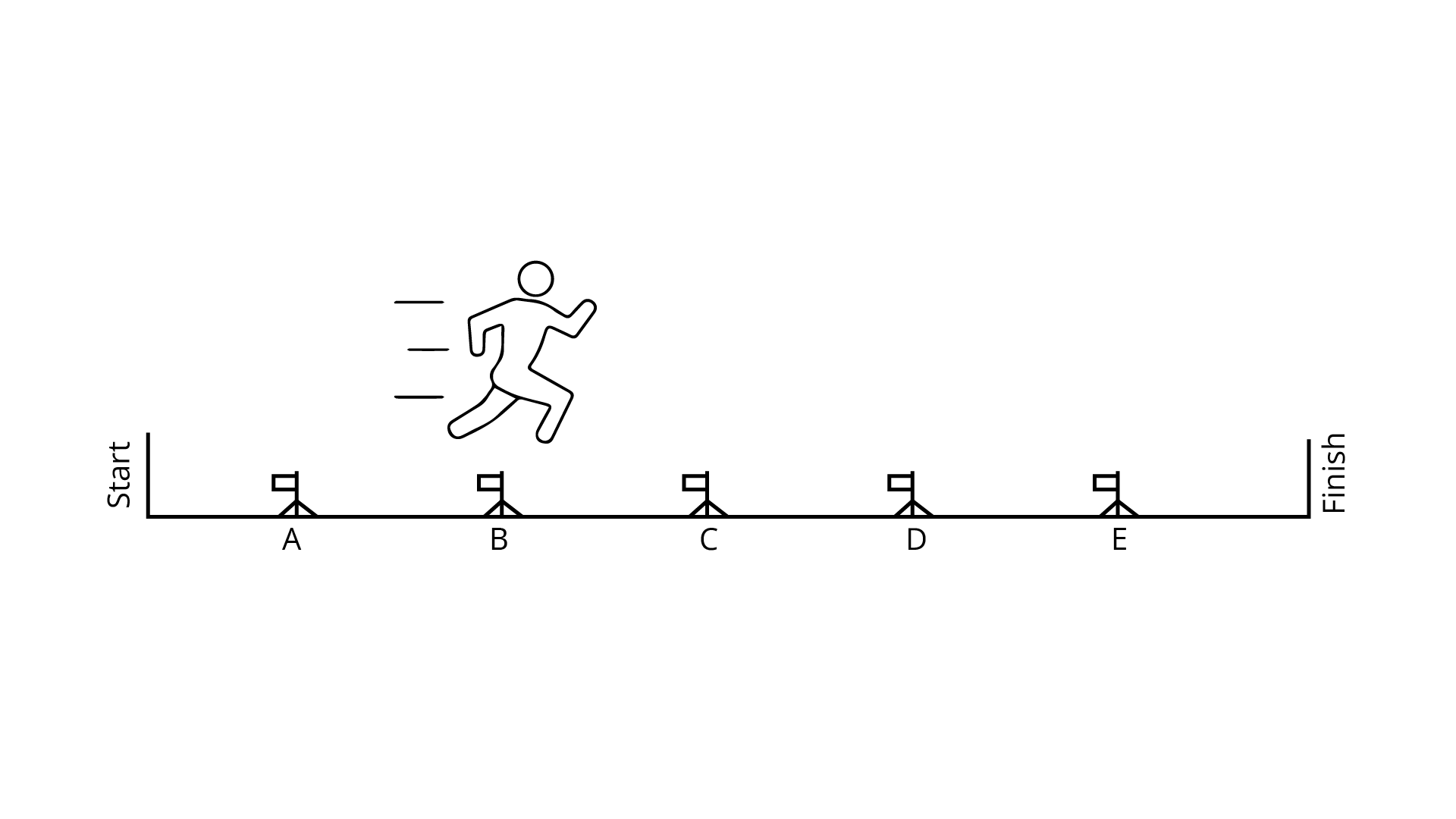
Then, answer the following:
(a) Where will Nidhi be, when she is $\dfrac{{\mathbf{4}}}{{\mathbf{6}}}$ on the way through the race?
Ans: Nidhi will be at hurdle D when she is $\dfrac{4}{6}$ on the way through the race.
(b) Where will Nidhi be when she is $\dfrac{{\mathbf{5}}}{{\mathbf{6}}}$ on the way through the race?
Ans: Nidhi will be at hurdle $E$ when she is $\dfrac{5}{6}$ on the way through the race.
(c) Give two fractions to tell what part of the race Nidhi has finished when she is over hurdle C.
Ans: When Nidhi will be at hurdle ${\text{C}}$, she would finished the $\dfrac{3}{6}$ or $\dfrac{1}{2}$ of the race.
74. Diameter of Earth is ${\mathbf{12756000\;m}}$. In 1996, a new planet was discovered whose diameter is of the diameter $\dfrac{{\mathbf{5}}}{{{\mathbf{86}}}}$ of Earth. Find the diameter of this planet in km.
Ans: Given, diameter of the earth is $12756000\;{\text{m}}$
Diameter of a new planet earth
$= \dfrac{5}{{86}} \times 12756000 = 741627.90\;{\text{m}}$
$\dfrac{{741627.90}}{{1000}} = 741.6\;{\text{km}}$
75. What is the product of $\dfrac{{\mathbf{5}}}{{{\mathbf{129}}}}$ and its reciprocal?
Ans: The reciprocal of $\dfrac{5}{{129}}$ is $\dfrac{{129}}{5}$
Now, the product is
$\dfrac{5}{{129}} \times \dfrac{{129}}{5} = 1$
76. Simplify: $\dfrac{{{\mathbf{2}}\dfrac{{\mathbf{1}}}{{\mathbf{2}}}{\mathbf{ + }}\dfrac{{\mathbf{1}}}{{\mathbf{5}}}}}{{{\mathbf{2}}\dfrac{{\mathbf{1}}}{{\mathbf{2}}}{\mathbf{ \div }}\dfrac{{\mathbf{1}}}{{\mathbf{5}}}}}$
Ans: The simplification of the fraction $\dfrac{{2\dfrac{1}{2} + \dfrac{1}{5}}}{{2\dfrac{1}{2} \div \dfrac{1}{5}}} = \dfrac{{\dfrac{5}{2} + \dfrac{1}{5}}}{{\dfrac{5}{2} \div \dfrac{1}{5}}}$
$= \dfrac{{27}}{{10}} \times \dfrac{2}{{25}}$
$= \dfrac{{27}}{{125}}$
77. Simplify: $\dfrac{{\dfrac{1}{4} + \dfrac{1}{5}}}{{1 - \dfrac{3}{8} \times \dfrac{3}{5}}}$
Ans: The simplification of fraction
$\dfrac{{\dfrac{1}{4} + \dfrac{1}{5}}}{{1 - \dfrac{3}{8} \times \dfrac{3}{5}}} = \dfrac{{\dfrac{1}{4} + \dfrac{1}{5}}}{{1 - \dfrac{9}{{40}}}}$
$= \dfrac{{\dfrac{{5 + 4}}{{20}}}}{{\dfrac{{40 - 9}}{{40}}}}$
$= \dfrac{9}{{20}} \times \dfrac{{40}}{{31}}$
$= \dfrac{{18}}{{31}}$
78. Divide $\dfrac{{\mathbf{3}}}{{{\mathbf{10}}}}$ by $\left( {\dfrac{{\mathbf{1}}}{{\mathbf{4}}}} \right.$ of $\left. {\dfrac{{\mathbf{3}}}{{\mathbf{5}}}} \right)$
Ans: The division of fractions
$\dfrac{3}{{10}} \div \left( {\dfrac{1}{4} \times \dfrac{3}{5}} \right) = \dfrac{3}{{10}} \div \dfrac{3}{{20}}$
$= \dfrac{3}{{10}} \times \dfrac{{20}}{3} = 2$
79. $\dfrac{{\mathbf{1}}}{{\mathbf{8}}}$ of a number equals $\dfrac{{\mathbf{2}}}{{\mathbf{5}}}{\mathbf{ \div }}\dfrac{{\mathbf{1}}}{{{\mathbf{20}}}}$. What is the number?
Ans: Let the number be $x$
$\dfrac{1}{8} \times x = \dfrac{2}{5} \div \dfrac{1}{{20}}$
$\dfrac{x}{8} = \dfrac{2}{5} \times \dfrac{{20}}{1}$
$\dfrac{x}{8} = 8$
$x = 64$
Therefore, the required number is $64.$
80. Heena's father paid an electric bill of ₹ ${\mathbf{385}}{\mathbf{.70}}$ out of a ${\mathbf{500}}$ rupee note. How much change should he have received?
Ans: The amount Heena's father has Rs $500$
The amount spent in electricity bill Rs. $385.70$
Therefore, the remaining money
$Rs.(500 - 385.70) = 114.30$
81. The normal body temperature is ${\mathbf{98}}.{\mathbf{6}}^\circ {\mathbf{F}}$. When Savitri was ill her temperature rose to ${\mathbf{103}}.{\mathbf{1}}^\circ {\mathbf{F}}$. How many degrees above normal was that?
Ans: Given data
${98.6^\circ }{\text{F}}$ is the normal body temperature
${103.1^\circ }{\text{F}}$ was the body temperature of Savitri, when she was ill.
For the normal
${103.1^\circ }{\text{F}} - {98.6^\circ }{\text{F}} = {4.5^\circ }{\text{F}}$
82. Meteorology: One measure of average global temperature shows how each year varies from a base measure. The table shows results for several years.
Year | \[1958\] | \[1964\] | \[1965\] | \[1978\] | \[2002\] |
Difference from Base | ${0.10^ \circ }C$ | $ - {0.17^ \circ }C$ | $ - {0.10^ \circ }C$ | ${\left( {\dfrac{1}{50}} \right)^\circ }{\text{C}}$ | ${0.54^ \circ }C$ |
See the table and answer the following:
(a) Order the five years from coldest to warmest.
Ans: From coldest to warmest.
$1964,1965,1978,1958,2002$ were the orders of five years from coldest to warmest.
(b) In ${\mathbf{1946}}$ the average temperature varied by $ - {0.03}^{\circ}C$ from the base measure. Between which two years should ${\mathbf{1946}}$ fall when the years are ordered from coldest to warmest?
Ans: In $1946,$ The average temperature variation is $ - {0.03^\circ }{\text{C}}$
Then $ - {0.10^\circ }{\text{C}} < - {0.03^\circ }{\text{C}} < {\left( {\dfrac{1}{{50}}} \right)^\circ }{\text{C}}$
Therefore, $1946$ should lies between $1965$and $1978$
83. In her science class, Jyoti learned that the atomic weight of Helium is \[{\mathbf{4}}.{\mathbf{0030}}\]. of Hydrogen is \[{\mathbf{1}}.{\mathbf{0080}}\] and of Oxygen is \[{\mathbf{16}}.{\mathbf{0000}}\]. Find the difference between the atomic weights of:
(a) Oxygen and Hydrogen
Ans: Given,
Atomic weight of Hydrogen is $1.0080$
Atomic weight of Helium is $4.0030$
Atomic weight of Oxygen is $16.0000$
The difference of weight of Oxygen and Hydrogen
$= 16.0000 - 1.0080 = 14.9920$
(b) Oxygen and Helium
Ans: The difference of weight of Oxygen and Helium
$= 16.0000 - 4.0030 = 11.9970$
(c) Helium and Hydrogen
Ans: The difference of weight of Helium and Hydrogen
$4.0030 - 1.0080 = 2.9950$
84. Measurements made in the science lab must be as accurate as possible. Ravi measured the length of an iron rod and said it was ${\mathbf{19}}{\mathbf{.34\;cm}}$ long; Kamal said ${\mathbf{19}}{\mathbf{.25\;cm}}$; and Tabish said ${\mathbf{19}}{\mathbf{.27\;cm}}$. The correct length was ${\mathbf{19}}{\mathbf{.33\;cm}}$. How much error was made by each of the boys?
Ans: Iron rod's correct length is $19.33\;{\text{cm}}$.
The length of rod measured by Kamal $= 19.25\;{\text{cm}}$
Therefore, the error made by the Kamal
$19.25 - 19.33 = - 0.08\;{\text{cm}}$
The length of rod measured by Tabish $= 19.27\;{\text{cm}}$
Therefore, the error made by Tabish
$19.27 - 19.33 = - 0.06\;{\text{cm}}$
The length of rod measured by Ravi $= 19.34\;{\text{cm}}$
Therefore, the error made by the Ravi
$19.34 - 19.33 = + 0.01\;{\text{cm}}$
85. When ${\mathbf{0}}{\mathbf{.02964}}$ is divided by ${\mathbf{0}}{\mathbf{.004}}$, what will be the quotient?
Ans: By division
$\dfrac{{0.02964}}{{0.004}} = \dfrac{{2964}}{{100000}} \div \dfrac{4}{{1000}}$
$= \dfrac{{2964}}{{100000}} \times \dfrac{{1000}}{4}$
$= \dfrac{{741}}{{100}}$
$= 7.41$
86. What number divided by ${\mathbf{520}}$ gives the same quotient as ${\mathbf{85}}$ divided by ${\mathbf{0}}{\mathbf{.625?}}$
Ans: Let number ${\text{Y}}$ be $520$
$Y \div 520 = 85 \div 0.625$
$\dfrac{y}{{520}} = \dfrac{{85}}{{0.625}}$
$ y = \dfrac{{44200}}{{625}} \times 1000$
$= 70.72 \times 1000$
$= 70720$
87. A floor is ${\mathbf{4}}{\mathbf{.5\;m}}$ long and ${\mathbf{3}}{\mathbf{.6\;m}}$ wide. ${\kern 1pt} {\kern 1pt} {\mathbf{A}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\mathbf{6\;cm}}$ square tile costs\[{\mathbf{23}}{\mathbf{.25}}\]. What will be the cost to cover the floor with these tiles?
Ans: Length of floor is $4.5m \times 100 = 450\;{\text{cm}}$
Width of the floor $= 3.6\;{\text{m}} = (3.6 \times 100) = 360\;{\text{cm}}$
Hence, Area of the floor $= 360 \times 450 = 162000\;{\text{c}}{{\text{m}}^2}$
Side of the square tile $= 6\;{\text{cm}}$
Now, one square tile of cost $= 6 \times 6 = 36\;{\text{c}}{{\text{m}}^2}$
Number of tiles required to cover the floor
$= \dfrac{{{\text{ Area of floor }}}}{{{\text{ Area of onetile }}}} = \dfrac{{16200}}{{36}} = 4500$
Now, the cost of one tile is Rs. $23.25$
Therefore, the cost of $4500$ tiles
$23.25 \times 4500 = {\text{ Rs}}.104625$
88. Sunita and Rehana want to make dresses for their dolls. Sunita has $\dfrac{{\mathbf{3}}}{{\mathbf{4}}}{\mathbf{\;m}}$ of cloth, and she gave $\dfrac{{\mathbf{1}}}{{\mathbf{3}}}$ of it to Rehana. How much did Rehana have?
Ans: Sunita has the length of clothes $= \dfrac{3}{4}m$
So, the Rehana's cloth length $= \dfrac{1}{3}{\text{ of }}\dfrac{3}{4}m = \dfrac{1}{3} \times \dfrac{3}{4}$
$= \dfrac{1}{4}m$
89. A flower garden is ${\mathbf{22}}{\mathbf{.50\;m}}$ long. Sheela wants to make a border along one side using bricks that are ${\mathbf{0}}{\mathbf{.25\;m}}$ long. How many bricks will be needed?
Ans: The garden has the length of $= 22.50\;{\text{m}}$
Length of one brick $= 0.25\;{\text{m}}$
So, the No. of brick requires making the border
$= \dfrac{{{\text{ length of the garden }}}}{{{\text{ Length of one brick }}}}$
$= \dfrac{{22.50}}{{0.25}} = \dfrac{{2250}}{{25}} = 90$
90. How much cloth will be used in making 6 shirts, if each required ${\mathbf{2}}\dfrac{{\mathbf{1}}}{{\mathbf{4}}}{\mathbf{\;m}}$ of cloth, allowing $\dfrac{{\mathbf{1}}}{{\mathbf{8}}}{\mathbf{\;m}}$ for waste in cutting and finishing in each shirt?
Ans: Length of cloth required for one shirt
$= 2\dfrac{1}{4}m + \dfrac{1}{8}m = \left( {\dfrac{9}{4} + \dfrac{1}{8}} \right)$
$= \left( {\dfrac{{18 + 1}}{8}} \right)$
$= \dfrac{{19}}{8}m$
Hence, the length of cloth required for six shirts
$= \dfrac{{19}}{8} \times 6 = \dfrac{{19 \times 3}}{4}m$
$= \dfrac{{57}}{4}$
$= 14\dfrac{1}{4}m$
91. A picture hall has seats for ${\mathbf{820}}$ persons. At a recent film show, one usher guessed it was $\dfrac{{\mathbf{3}}}{{\mathbf{4}}}$ full, another that it was $\dfrac{{\mathbf{2}}}{{\mathbf{3}}}$ full. The ticket office reported ${\mathbf{648}}$ sales. Which usher (first or second) made the better guess?
Ans: Total no. of seats $= 820$
Total ticket's sale $= 648$
The first usher guessed the number of sold tickets
$= \dfrac{3}{4} \times 820 = 615$
The second usher guessed the number of sold tickets
$= \dfrac{2}{3} \times 820 = \dfrac{{1640}}{3}$
$= 546.66 \approx 547$
So, $615$ is near to $648$ than $547$
So, the first usher guessed better.
92. For the celebrating children's students of Class VII bought sweets for Rs.${\mathbf{740}}{\mathbf{.25}}$and cold drink for ₹ \[{\mathbf{70}}.\]If ${\mathbf{35}}$ students contributed equally what amount was contributed by each student?
Ans: The total amount spent on children day
$= 740.25 + 70 = 810.25$
Number of students who made contribution $= 35$
So, the contribution of each student $= \dfrac{{810.25}}{{35}}$
$= Rs.23.15$
93. The time taken by Rohan in five different races to run a distance of ${\mathbf{500\;m}}$ was ${\mathbf{3}}{\mathbf{.20}}$minutes, \[{\mathbf{3}}{\mathbf{.37}}\]minutes, ${\mathbf{3}}{\mathbf{.29}}$minutes, ${\mathbf{3}}{\mathbf{.17}}$ minutes and ${\mathbf{3}}{\mathbf{.32}}$ minutes. Find the average time taken by him in the races.
Ans: Total number of races is $5.$
In five races time taken by Rohan
$3.20 + 3.37 + 3.29 + 3.17 + 3.32$
$= 16.35$
The average time taken by Rohan $= \dfrac{{16.35}}{5}$
$= 3.27$ minutes
94. A public sewer line is being installed along ${\mathbf{80}}\dfrac{{\mathbf{1}}}{{\mathbf{4}}}{\mathbf{\;m}}$ of road. The supervisor says that the laborers will be able to complete ${\mathbf{7}}{\mathbf{.5\;m}}$ in one day. How long will the project take to complete?
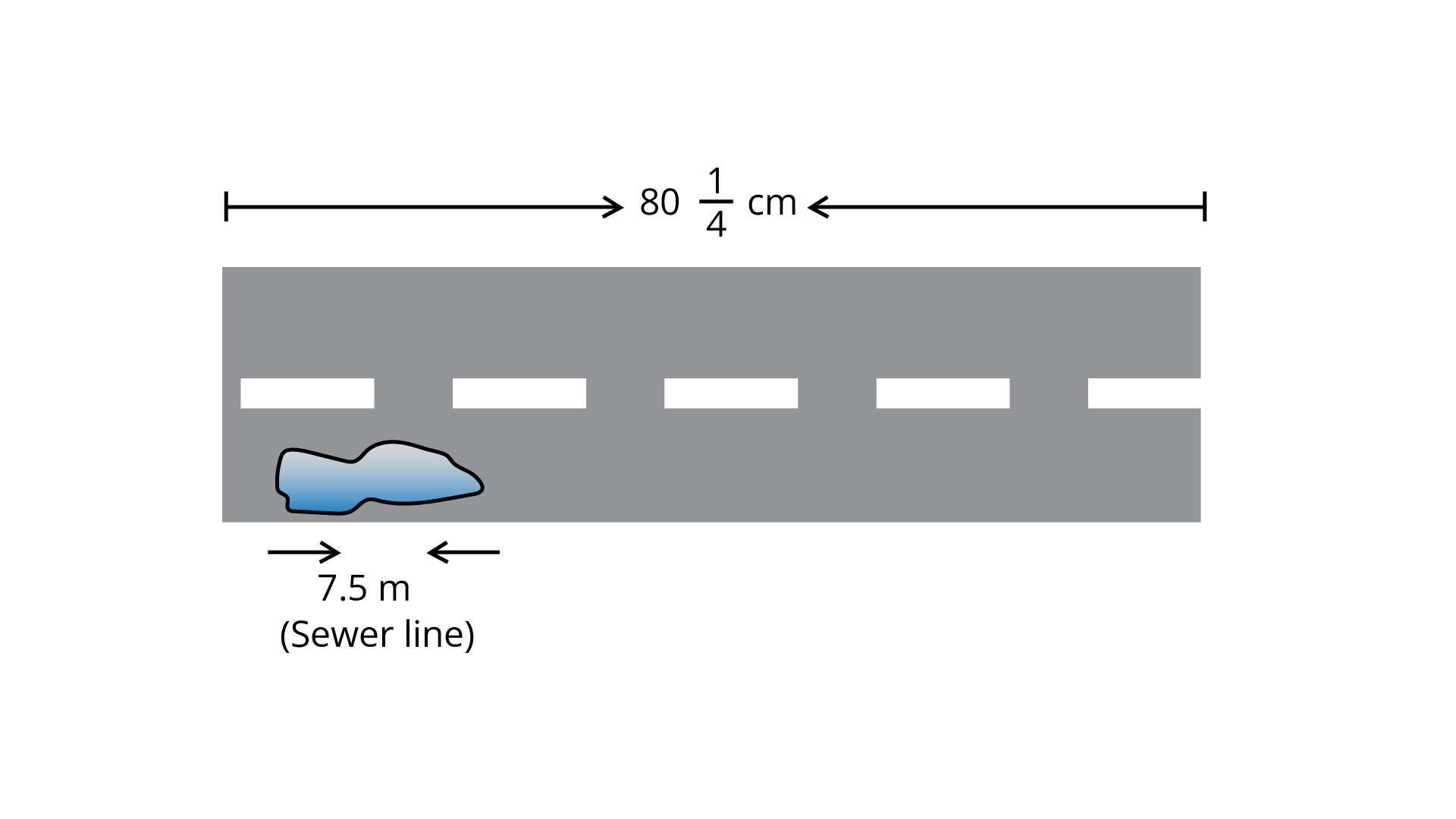
Ans: The sewer lines length $= 80\dfrac{1}{4} = \dfrac{{321}}{4}\;{\text{m}}$
Given $7.5\;{\text{m}}$ long sewer can made in one day
So, $\dfrac{{321}}{4}$ meter long sewer takes the time of
$\dfrac{1}{{7.5}} \times \dfrac{{321}}{4} = \dfrac{{3210}}{{300}}$
$= 10.7 \approx 11{\text{ days }}$
95. The weight of an object on the moon is $\dfrac{{\mathbf{1}}}{{\mathbf{6}}}$ its weight on Earth. If an object weighs ${\mathbf{5}}\dfrac{{\mathbf{3}}}{{\mathbf{5}}}{\mathbf{\;kg}}$ on Earth, how much would it weigh on the moon?
Ans: Weight of the object on the earth $= 5\dfrac{3}{5} = \dfrac{{28}}{5}\;{\text{kg}}$
So, weight of that particular object on the moon
$= \dfrac{1}{6} \times \dfrac{{28}}{5} = \dfrac{{14}}{{15}}$
$= 0.93\;{\text{kg}}$
96. In a survey, ${\mathbf{200}}$ students were asked what influenced them most to buy their latest CD. The results are shown in the circle graph.

(a) How many students said radio influenced them most?
Ans: From flow chart
The no. of students, influenced by radio
$\dfrac{9}{{20}} \times 200 = 90$
(b) How many more students were influenced by radio than by a music video channel?
Ans: The no. of students, influenced by music video channel
$\dfrac{2}{{25}} \times 200 = 16$
(c) How many said a friend or relative influenced them or they heard the CD in a shop?
Ans: The no. of students, influenced by relative or friend
$\dfrac{3}{{20}} \times 200 = 30$
The no. of students, influenced by seeing or hearing CD in shop
$= \dfrac{1}{{10}} \times 200 = 20$
Therefore, the total number of students who were influenced by both
$= 30 + 20 = 50$
97. In the morning, a milkman filled ${\mathbf{5}}\dfrac{{\mathbf{1}}}{{\mathbf{2}}}L$ of milk in his can. He sold to Renu, Kamla and Renuka $\dfrac{{\mathbf{3}}}{{\mathbf{4}}}{\mathbf{L}}$ each; to Shadma he sold $\dfrac{{\mathbf{7}}}{{\mathbf{8}}}{\mathbf{\;L;}}$ and to Jassi he gave ${\mathbf{1}}\dfrac{{\mathbf{1}}}{{\mathbf{2}}}L$. How much milk is left in the can?
Ans: The container can contain the total quantity of milk
$= 5\dfrac{1}{2}L = \dfrac{{11}}{2}L$
The total quantity to be sold
$= \left( {\dfrac{3}{4} + \dfrac{3}{4} + \dfrac{3}{4} + \dfrac{7}{8} + 1\dfrac{1}{2}} \right)$
$= \left( {\dfrac{{18 + 7 + 12}}{8}} \right) = \dfrac{{37}}{8}L$
Now, quantity of milk left in the milk can
$= \left( {\dfrac{{11}}{2} - \dfrac{{37}}{8}} \right) = \dfrac{{44 - 37}}{8}$
$= \dfrac{7}{8}L$
98. Anuradha can do a piece of work in ${\mathbf{6}}$ hours. What part of the work can she do in $\mathbf{1}$ hour, in ${\mathbf{5}}$ hours, in ${\mathbf{6}}$ hours?
Ans: ${\text{X}}$ is the part of work done by Anuradha in 6 hours
Then, work done in an hour $= \dfrac{X}{6}$
The part of work done in 5 hours $= \dfrac{5}{6}X$
The part of work done in 6 hours $= \dfrac{X}{6} \times 6 = X$
So, Anuradha can do $\dfrac{1}{6}$ part of work in 1 hour,
$\dfrac{5}{6}$ part of work in 5 hours and 6 hours to be taken for complete work done.
99. What portion of a 'saree' can Rehana paint in 1 hour if it requires 5 hours to paint the whole saree? In ${\mathbf{4}}\dfrac{{\mathbf{3}}}{{\mathbf{5}}}$ hours? In ${\mathbf{3}}\dfrac{{\mathbf{1}}}{{\mathbf{2}}}$ hours?
Ans: Rehana painted, 1 portion of saree in 5 hours
Hence, the portion of saree painted by her in an hour $= \dfrac{1}{5}$
Then portion of saree painted by her in
$4\dfrac{3}{5}{\text{ hours }} = \dfrac{1}{5} \times 4\dfrac{3}{5} = \dfrac{{23}}{{25}}$
The portion of saree painted by her
$3\dfrac{1}{2}{\text{ hours }} = \dfrac{1}{5} \times 3\dfrac{1}{2} = \dfrac{7}{{10}}$
100. Rama has ${\mathbf{6}}\dfrac{{\mathbf{1}}}{{\mathbf{4}}}{\mathbf{\;kg}}$ of cotton wool for making pillows. If one pillow takes ${\mathbf{1}}\dfrac{{\mathbf{1}}}{{\mathbf{4}}}{\mathbf{\;kg}}$, how many pillows can she make?
Ans: Given, total quantity of cotton wool $= 6\dfrac{1}{4} = \dfrac{{25}}{4}\;{\text{kg}}$
The wool required for 1 pillow
$\dfrac{{25}}{4} \div \dfrac{5}{4} = \dfrac{{25}}{4} \times \dfrac{4}{5}$
$= 5$
101. It takes ${\mathbf{2}}\dfrac{{\mathbf{1}}}{{\mathbf{3}}}{\mathbf{\;m}}$ of cloth to make a shirt. How many shirts can Radhika make from a piece of cloth ${\mathbf{9}}\dfrac{{\mathbf{1}}}{{\mathbf{3}}}{\mathbf{\;m}}$ long?
Ans: Given, the length of cloth is $9\dfrac{1}{3}$ meter
The length of shirt required to make a cloth $= 2\dfrac{1}{3} = \dfrac{{7}}{3}m$
Then required number of shirts
$= \dfrac{{28}}{3} \div \dfrac{7}{3}$
$= \dfrac{{28}}{3} \times \dfrac{3}{7}$
$= 4$
102. Ravi can walk ${\mathbf{3}}\dfrac{{\mathbf{1}}}{{\mathbf{3}}}{\mathbf{\;km}}$ in one hour. How long will it take him to walk to his office which is ${\mathbf{10\;km}}$ from his home?
Ans: Time taken by him to walk $1\;{\text{km}}$
$\left( {1 \div 3\dfrac{1}{3}} \right) = \left( {1 \div \dfrac{{10}}{3}} \right){\text{ hours }}$
$= \left( {1 \times \dfrac{3}{{10}}} \right) = \dfrac{3}{{10}}{\text{ hours }}$
So, time taken by Ravi to walk $10\;{\text{km}}$
$= \left( {10 \times \dfrac{3}{{10}}} \right) = 3$ hours
103. Raj travels ${\mathbf{360km}}$ on three fifths of his petrol tank. How far would he travel at the same rate with a full tank of petrol?
Ans: Raj travels $360\;{\text{km}}$ with $\dfrac{3}{5}$ filled tank of petrol When tank is full with petrol the distance he travels
$\left( {360 \div \dfrac{3}{5}} \right) = \dfrac{{360 \times 5}}{3}$
$= 120 \times 5$
$= 600\;{\text{km}}$
104. Kajol has ₹$\[{\mathbf{75}}\]. This is \[\dfrac{{\mathbf{3}}}{{\mathbf{8}}}\] of the amount she earned. How much did she earn?
Ans: Let Kajol earned x money
$\dfrac{3}{8} \times x = 75$
$x = 75 \times \dfrac{8}{3}$
$x = 200$
Kajol earned the amount of $200.$
105. It takes 17 full specific types of trees to make one tonne of paper. If there are \[{\mathbf{221}}\]
such trees in a forest, then
(i) what fraction of forest will be used to make;
(a) \[{\mathbf{5}}\] tonnes of paper.
Ans: The making of one tonne of paper requires $17$ trees
Total given number of trees is \[221\]
Hence, fraction of forest will used to make one tones of paper
$= \dfrac{{17}}{{221}} = \dfrac{1}{{13}}$
Fraction of forest will used to make 5 tons of paper
$= \dfrac{1}{{13}} \times 5 = \dfrac{5}{{13}}$
(b) ${\mathbf{10}}$ tonnes of paper.
Ans: Fraction of forest will used to make 10 tons of paper
$= \dfrac{1}{{13}} \times 10 = \dfrac{{10}}{{13}}$
(ii) To save $\dfrac{{\mathbf{7}}}{{{\mathbf{13}}}}$ part of the forest how much paper we have to save.
Ans: We have ${\text{X}}$ tons of paper to save $\dfrac{7}{{13}}$ part of forest
Fraction of forest will used to make ${\text{X}}$ tons of paper $\dfrac{1}{{13}} \times X = \dfrac{X}{{13}}$
Now,
$\dfrac{X}{{13}} = \dfrac{7}{{13}}$
$X = \dfrac{7}{{13}} \times 13 = 7$
106. Simplify and write the result in decimal form :
$\left( {{\mathbf{1 \div }}\dfrac{{\mathbf{2}}}{{\mathbf{9}}}} \right){\mathbf{ + }}\left( {{\mathbf{1 \div 3}}\dfrac{{\mathbf{1}}}{{\mathbf{5}}}} \right){\mathbf{ + }}\left( {{\mathbf{1 \div 2}}\dfrac{{\mathbf{2}}}{{\mathbf{3}}}} \right)$
Ans: Given,
$\left( {1 \div \dfrac{2}{9}} \right) + \left( {1 \div 3\dfrac{1}{5}} \right) + \left( {1 \div 2\dfrac{2}{3}} \right)$
$= \left( {1 \times \dfrac{9}{2}} \right) + \left( {1 \div \dfrac{{16}}{5}} \right) + \left( {1 \div \dfrac{8}{3}} \right)$
$= \dfrac{9}{2} + \dfrac{5}{{16}} + \dfrac{3}{8}$
$= \dfrac{{72 + 5 + 6}}{{16}}$
$= \dfrac{{83}}{{16}} = 5.1875$
107. Some pictures (a) to (f) are given below. Tell which of them show:
(1) ${\mathbf{2}} \times \dfrac{{\mathbf{1}}}{{\mathbf{4}}}$
(2) ${\mathbf{2 \times }}\dfrac{{\mathbf{3}}}{{\mathbf{7}}}$
(3) ${\mathbf{2 \times }}\dfrac{{\mathbf{1}}}{{\mathbf{3}}}$
(4) $\dfrac{{\mathbf{1}}}{{\mathbf{4}}}{\mathbf{ \times 4}}$
(5) ${\mathbf{3 \times }}\dfrac{{\mathbf{2}}}{{\mathbf{9}}}$
(6) $\dfrac{{\mathbf{1}}}{{\mathbf{4}}}{\mathbf{ \times 3}}$
(a)
(b)
(c)

(d)

(e)
(f)
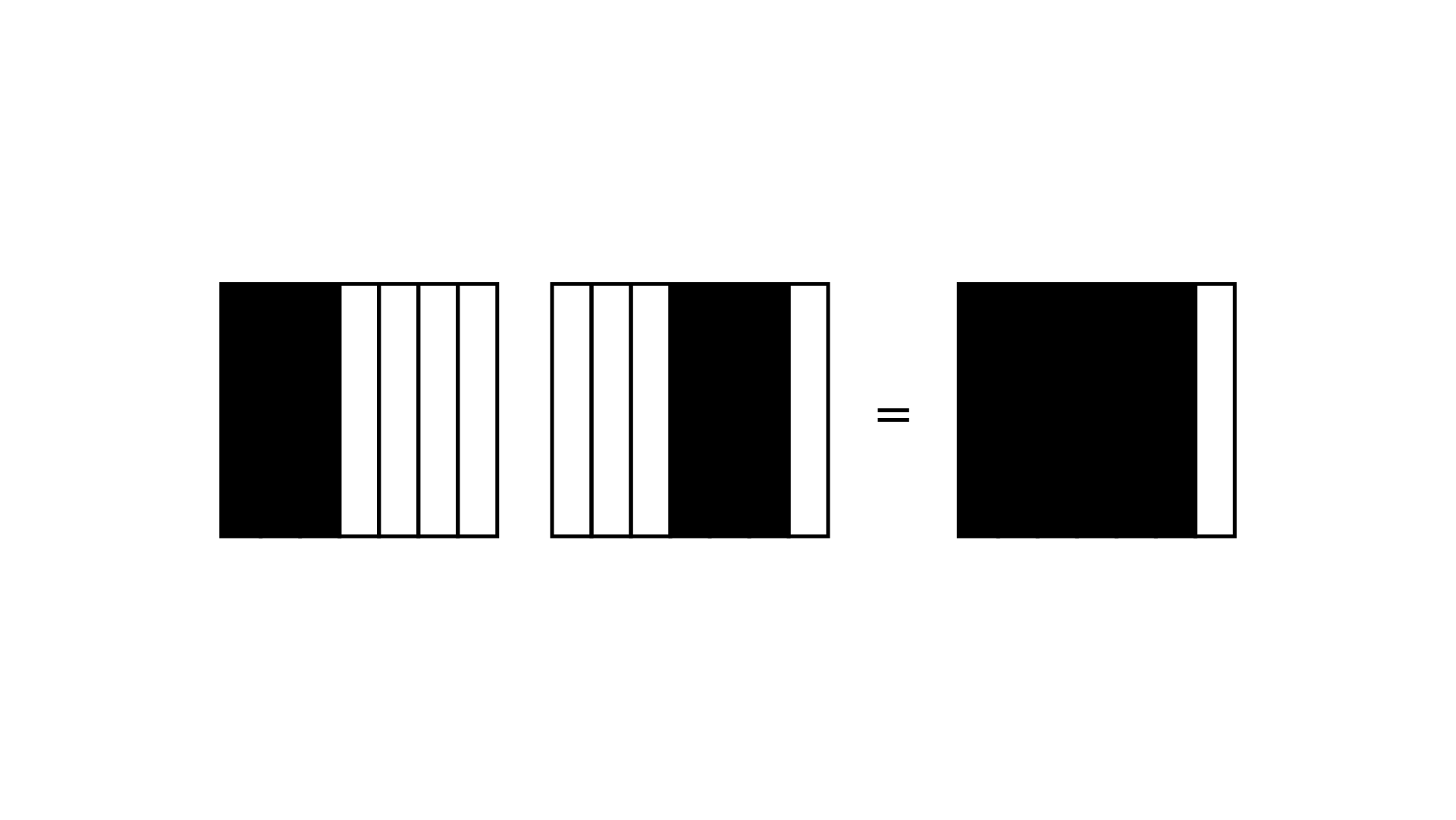
Ans: 1. $2 \times \dfrac{1}{4}$ represents:
i) Addition of 2 figures
ii) 1 shaded part out of 4 equal parts
iii) Represents by figure ${\text{d}}$
2. $2 \times \dfrac{3}{7}$ represents:
i) Addition of 2 figures
ii) 3 shaded parts out of 7 equal parts
iii) Represents by figure ${\text{f}}$
3. $2 \times \dfrac{1}{3}$ represents:
i) Addition of 2 figures
ii) 1 shaded part out of 3 equal parts
iii) Represents by figure ${\text{c}}$
4. $\dfrac{1}{4} \times 4$ represents:
i) Addition of 4 figures
ii) 1 shaded part out of 4 equal parts
iii) Represents by figure $b$
5. $3 \times \dfrac{2}{9}$ represents:
i) Addition of 3 figures
ii) 2 shaded part out of 9 equal parts
iii) Represents by figure a
6. $\dfrac{1}{4} \times 3$ represents:
i) Addition of 3 figures
ii) 1 shaded part out of 4 equal parts
iii) Represents by figure d
108. Evaluate: $\left( {{\mathbf{0}}{\mathbf{.3}}} \right){\mathbf{ \times (0}}{\mathbf{.3) - (0}}{\mathbf{.2) \times (0}}{\mathbf{.2)}}$
Ans: The decimal of $(0.3) \times (0.3) - (0.2) \times (0.2)$
$= \dfrac{3}{{10}} \times \dfrac{3}{{10}} - \left( {\dfrac{2}{{10}} \times \dfrac{2}{{10}}} \right)$
$= \dfrac{9}{{100}} - \dfrac{4}{{100}}$
$= \dfrac{5}{{100}} = 0.05$
109. Evaluate $\dfrac{{{\mathbf{0}}{\mathbf{.6}}}}{{{\mathbf{0}}{\mathbf{.3}}}}{\mathbf{ + }}\dfrac{{{\mathbf{0}}{\mathbf{.16}}}}{{{\mathbf{0}}{\mathbf{.4}}}}$
Ans: The fraction of $\dfrac{{0.6}}{{0.3}} + \dfrac{{0.16}}{{0.4}}$
$= \left( {\dfrac{6}{{10}} \times \dfrac{{10}}{3}} \right) + \left( {\dfrac{{16}}{{100}} \times \dfrac{{10}}{4}} \right)$
$= 2 + \dfrac{4}{{10}} = \dfrac{{20 + 4}}{{10}}$
$= \dfrac{{24}}{{10}} = 2.4$
110. Find the value of: $\dfrac{{{\mathbf{(0}}{\mathbf{.2 \times 0}}{\mathbf{.14) + (0}}{\mathbf{.5 \times 0}}{\mathbf{.91)}}}}{{{\mathbf{(0}}{\mathbf{.1 \times 0}}{\mathbf{.2)}}}}$
Ans: The fraction is $\dfrac{{(0.2 \times 0.14) + (0.5 + 0.91)}}{{(0.1 \times 0.2)}}$
$= \dfrac{{\left( {\dfrac{2}{{10}} \times \dfrac{{14}}{{100}}} \right) + \left( {\dfrac{5}{{10}} \times \dfrac{{91}}{{100}}} \right)}}{{\left( {\dfrac{1}{{10}} \times \dfrac{2}{{10}}} \right)}}$
$=\dfrac{\dfrac{28}{1000}+ \dfrac{455}{1000}}{\dfrac{2}{100}}$
$= \dfrac{{241.5}}{{10}} = 24.15$
111. A square and an equilateral triangle have a side in common. If side of triangle is $\dfrac{{\mathbf{4}}}{{\mathbf{3}}}{\mathbf{\;cm}}$ long, find the perimeter of figure formed (Fig. 2.8).
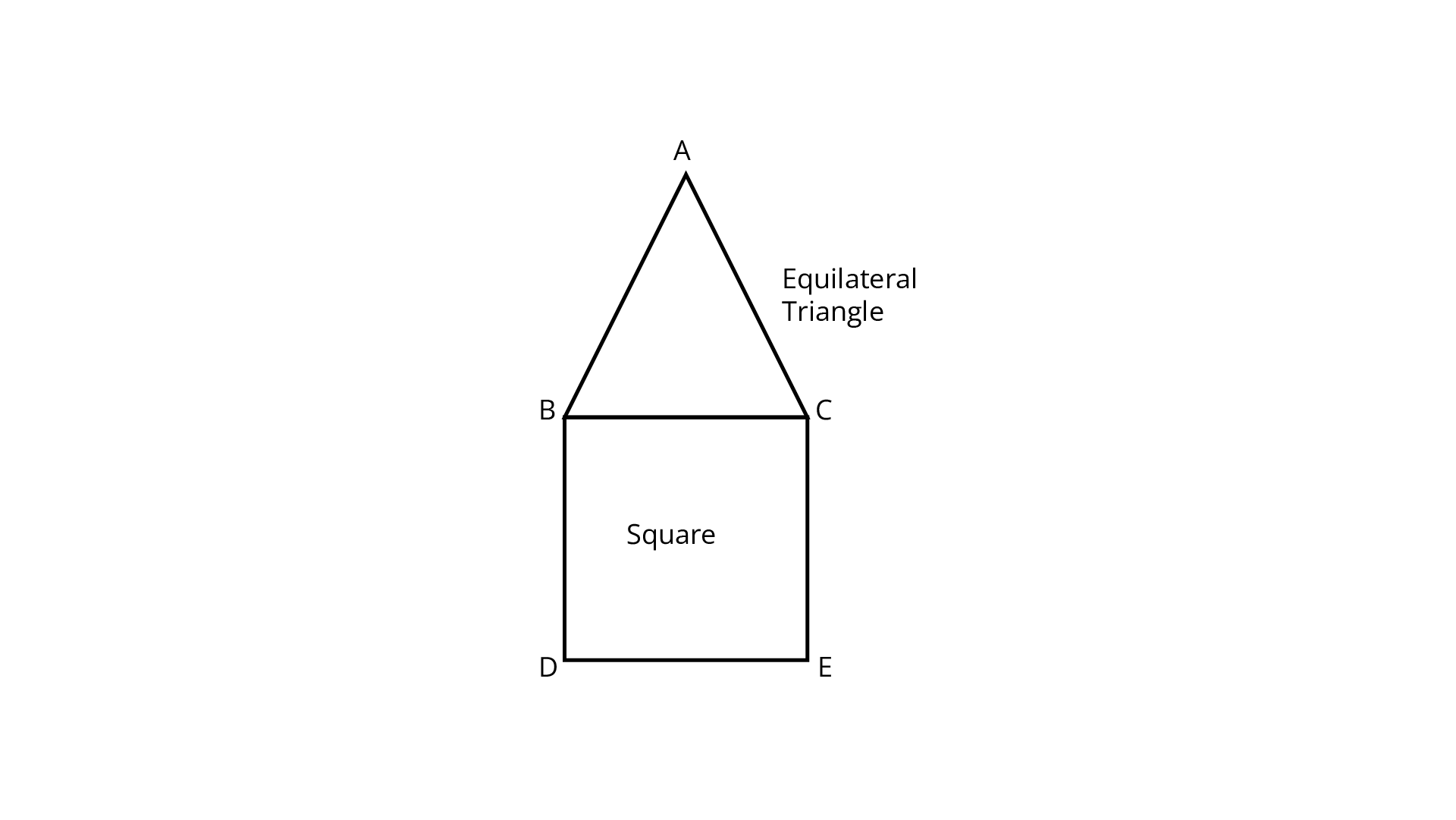
Ans: Sides of the equilateral triangle $= \dfrac{4}{3}\;{\text{cm}}$ Hence, square's side $= \dfrac{4}{3}\;{\text{cm}}$
Perimeter of the given figure $= \left( {\dfrac{4}{3} + \dfrac{4}{3} + \dfrac{4}{3} + \dfrac{4}{3} + \dfrac{4}{3}} \right)$
$= 5 \times \dfrac{4}{3}$
$= \dfrac{{20}}{3}$
$= 6\dfrac{2}{3}\;{\text{cm}}$
112. Rita has bought a carpet of size ${\mathbf{4\;m \times 6}}\dfrac{{\mathbf{2}}}{{\mathbf{3}}}{\mathbf{\;m}}$. But her room size is ${\mathbf{3}}\dfrac{{\mathbf{1}}}{{\mathbf{3}}}{\mathbf{\;m \times 5}}\dfrac{{\mathbf{1}}}{{\mathbf{3}}}{\mathbf{\;m}}$. What fraction of area should be cut off to fit wall to wall carpet into the room?
Ans: The area of the carpet $= 4 \times 6\dfrac{2}{3} = \dfrac{{80}}{3}\;{{\text{m}}^2}$
Area of room $= 3\dfrac{1}{3} \times 5\dfrac{1}{3}$
$= \dfrac{{10}}{3} \times \dfrac{{16}}{3}{m^2}$
$= \dfrac{{160}}{9}{m^2}$
Hence, area to be cut off $= \left( {\dfrac{{80}}{3} - \dfrac{{160}}{9}} \right){m^2}$
$=\dfrac{80}{9}{m}^{2}$
113. Family photograph has length ${\mathbf{14}}\dfrac{{\mathbf{2}}}{{\mathbf{5}}}{\mathbf{\;cm}}$ and breadth ${\mathbf{10}}\dfrac{{\mathbf{2}}}{{\mathbf{5}}}{\mathbf{\;cm}}$. It has border of uniform width ${\mathbf{2}}\dfrac{{\mathbf{3}}}{{\mathbf{5}}}{\mathbf{\;cm}}$. Find the area of the framed photograph.
Ans: Given data
Length of the photo $= 14\dfrac{2}{5} = \dfrac{{72}}{5}\;{\text{cm}}$
Breadth of photo $= 10\dfrac{2}{5} = \dfrac{{52}}{5}\;{\text{cm}}$
Length of framed photograph $= \left( {\dfrac{{72}}{5} + \dfrac{{13}}{5} + \dfrac{{13}}{5}} \right) = \dfrac{{98}}{5}\;{\text{cm}}$
Breadth of framed photograph $= \left( {\dfrac{{52}}{5} + \dfrac{{13}}{5} + \dfrac{{13}}{5}} \right) = \dfrac{{78}}{5}\;{\text{cm}}$
Hence, area of framed photograph $= \dfrac{{98}}{5} \times \dfrac{{78}}{5}$
$= \dfrac{{7644}}{{25}}$
$= 305\dfrac{{19}}{{25}}\;{\text{c}}{{\text{m}}^2}$
114. Cost of a burger is Rs ${\mathbf{20}}\dfrac{{\mathbf{3}}}{{\mathbf{4}}}$ and of Macduff is Rs ${\mathbf{15}}\dfrac{{\mathbf{1}}}{{\mathbf{2}}}$. Find the cost of 4 burgers and ${\mathbf{14}}$ mac puffs.
Ans: Cost of a burger $= 20\dfrac{3}{4}$. $= Rs{\kern 1pt} \,\dfrac{{83}}{4}$
Cost of a Mac Puffs $= 15\dfrac{1}{2} = Rs\dfrac{{31}}{2}$
Hence, cost of $4$ burgers $= \dfrac{{83}}{4} \times 4 = Rs.83$
and cost of $14$ Macduff's $= \dfrac{{31}}{2} \times 14 = Rs.217$
Therefore, total cost $= 217 + 83 = Rs.300$
115. A hill, ${\mathbf{101}}\dfrac{{\mathbf{1}}}{{\mathbf{3}}}{\mathbf{\;m}}$ in height, has $\dfrac{{\mathbf{1}}}{{\mathbf{4}}}$ th of its height under water. What is the height of the hill visible above the water?
Ans: Height of the hill $= 101\dfrac{1}{3}m = \dfrac{{304}}{3}m$
Hill's height under water $= \dfrac{1}{4} \times \dfrac{{304}}{3} = \dfrac{{76}}{3}m$
Therefore, hill visible above the water $= \left( {\dfrac{{304}}{3} - \dfrac{{76}}{3}} \right) = \dfrac{{228}}{3} = 76\;{\text{m}}$
116. Sports: Reaction time measures how quickly a runner reacts to the starter pistol. In the ${\mathbf{100\;m}}$ dash at the 2004 Olympic Games, Lauryn Williams had a reaction time of ${\mathbf{0}}{\mathbf{.214}}$ second. Her total race time, including reaction time, was ${\mathbf{11}}{\mathbf{.03}}$ seconds. How long did it take her to run the actual distance?
Ans: The race time of Lauryn Williams $= 11.03$ Seconds
Her reaction time $= 0.214$ Seconds
Hence, time required to run the actual distance
$= (11.03 - 0.214) = 10.816$ Seconds
117. State whether the answer is greater than 1 or less than 1. Put a mark in the appropriate box.
Questions | Greater than 1 | Less than 1 |
|---|---|---|
$\dfrac{2}{3} \div \dfrac{1}{2}$ | ||
$\dfrac{2}{3} \div \dfrac{2}{1}$ | ||
$6 \div \dfrac{1}{4}$ | ||
$\dfrac{1}{5} \div \dfrac{1}{2}$ | ||
$4\dfrac{1}{3} \div 3\dfrac{1}{2}$ | ||
$\dfrac{2}{3} \times 8\dfrac{1}{2}$ |
Ans: The answer is
1. $\dfrac{2}{3} \div \dfrac{1}{2} = \dfrac{2}{3} \times \dfrac{2}{1} = \dfrac{4}{3} > 1$
2. $\dfrac{2}{3} \div \dfrac{2}{1} = \dfrac{2}{3} \times \dfrac{1}{2} = \dfrac{1}{3} < 1$
3. $6 \div \dfrac{1}{4} = 6 \times 4 = 24 > 1$
4. $\dfrac{1}{5} \div \dfrac{1}{2} = \dfrac{1}{5} \times \dfrac{2}{1} = \dfrac{2}{5} < 1$
5. $4\dfrac{1}{3} \times 3\dfrac{1}{2} = \dfrac{{13}}{3} \times \dfrac{2}{7} = \dfrac{{26}}{{21}} > 1$
6. $\dfrac{2}{3} \times 8\dfrac{1}{2} = \dfrac{2}{3} \times \dfrac{{17}}{2} = \dfrac{{17}}{3} > 1$
Questions | Greater than 1 | Less than 1 |
$\dfrac{2}{3} \div \dfrac{1}{2}$ | yes | |
$\dfrac{2}{3} \div \dfrac{2}{1}$ | yes | |
$6 \div \dfrac{1}{4}$ | yes | |
$\dfrac{1}{5} \div \dfrac{1}{2}$ | yes | |
$4\dfrac{1}{3} \div 3\dfrac{1}{2}$ | yes | |
$\dfrac{2}{3} \times 8\dfrac{1}{2}$ | yes |
118. There are four containers that are arranged in the ascending order of their heights. If the height of the smallest container given in the figure is expressed as $\dfrac{{\mathbf{7}}}{{{\mathbf{25}}}}{\mathbf{x = 10}}{\mathbf{.5\;cm}}$. Find the height of the largest container.
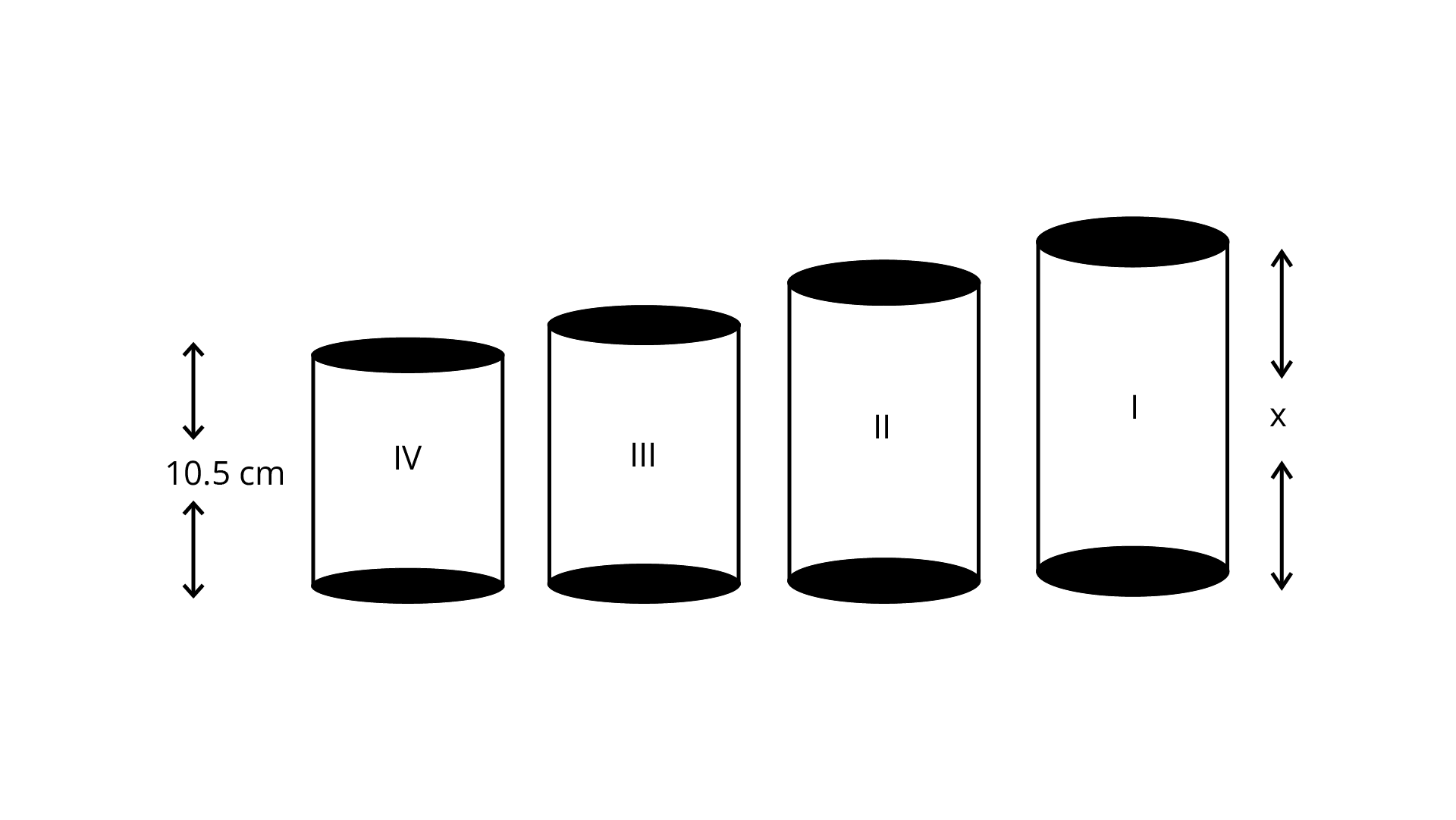
Ans: Given,
Height of the smaller container is $10.5\;{\text{cm}}$
$\dfrac{7}{{25}}x = 10.5$
$ x = \left( {10.5 \div \dfrac{7}{{25}}} \right)$
$= \left( {\dfrac{{105}}{{10}} \times \dfrac{25}{{7}}} \right)$
$= \dfrac{{375}}{{10}}\;{\text{cm}}$
So, the height of the largest container is $37.5\;{\text{cm}}$.
In Questions 119 to 122, replace '?' with appropriate fraction
119.
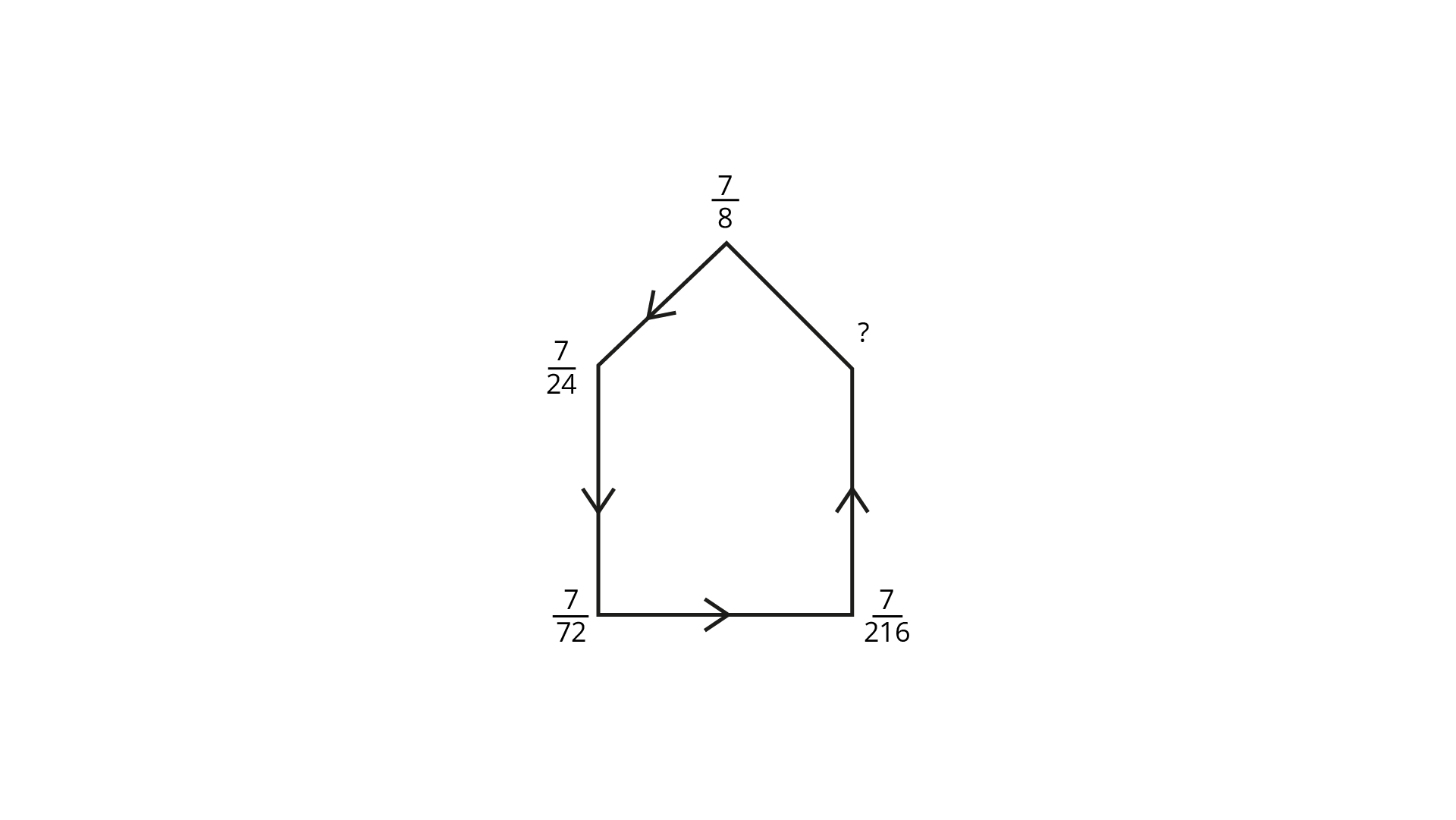
Ans: The given pattern, $\dfrac{7}{8}$,
$\dfrac{7}{{8 \times 3}} = \dfrac{7}{{24}}$,
$\dfrac{7}{{24 \times 3}} = \dfrac{7}{{72}}$,
$\dfrac{7}{{72 \times 3}} = \dfrac{7}{{216}}$
Next fraction is $\dfrac{7}{{216 \times 3}} = \dfrac{7}{{648}}$
120
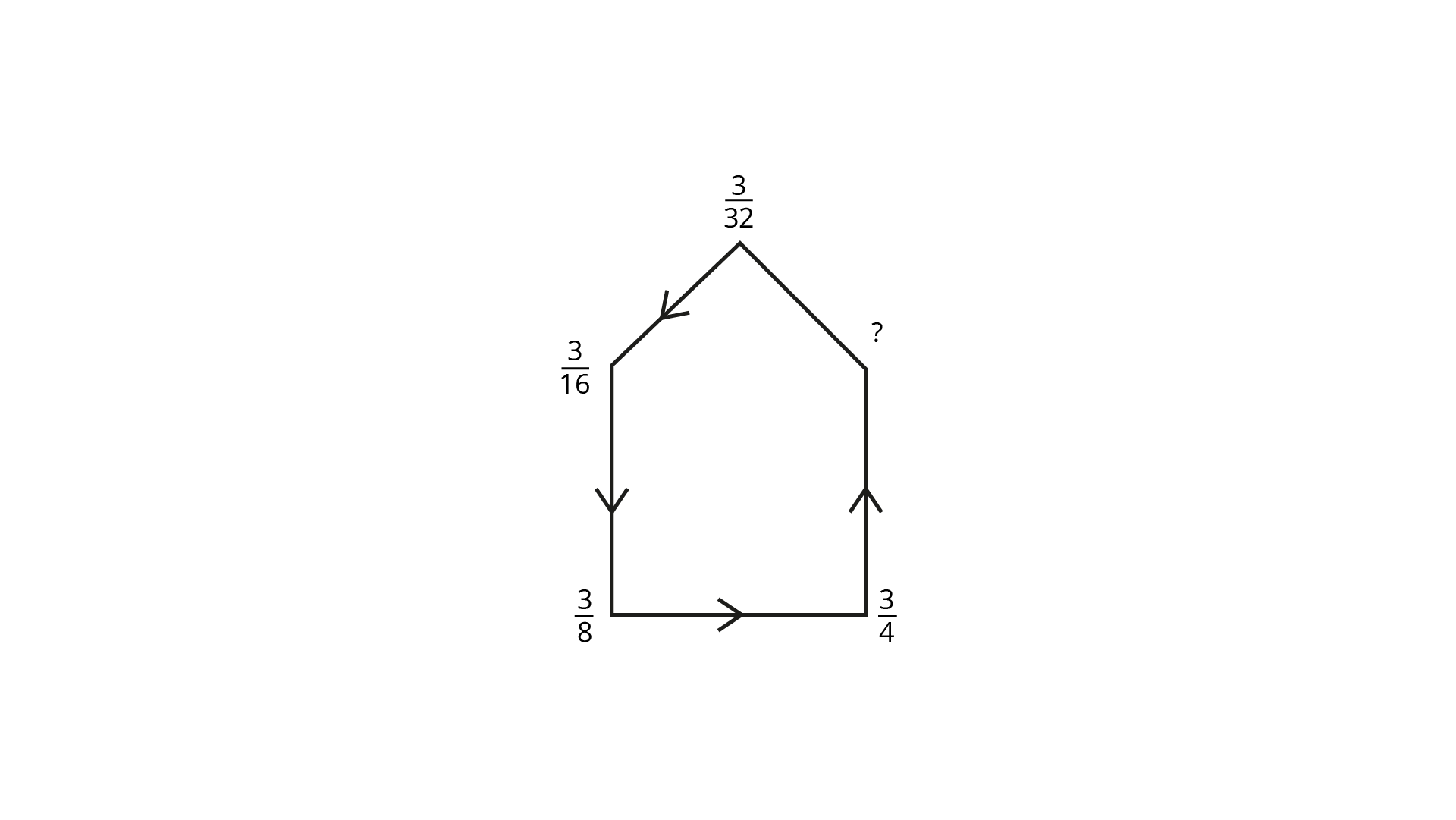
Ans: The given pattern,
$\dfrac{3}{{32}}$
$ \dfrac{3}{{32}} \times 2 = \dfrac{3}{{16}}$
$ \dfrac{3}{{16}} \times 2 = \dfrac{3}{8},$
$ \dfrac{3}{8} \times 2 = \dfrac{3}{4}$
So, Next fraction is $\dfrac{3}{4} \times 2 = \dfrac{3}{2}$
121
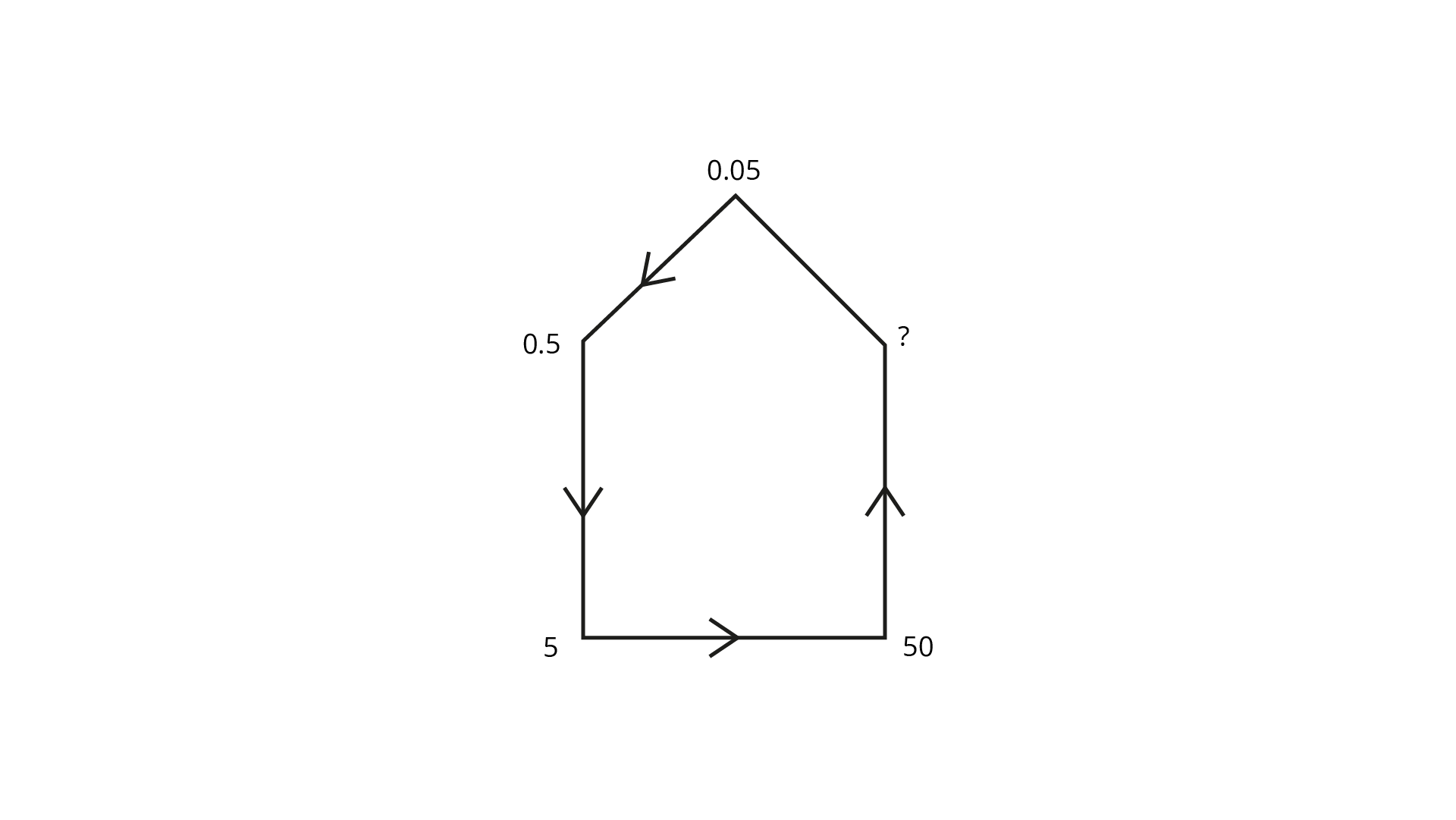
Ans: The given pattern
$0.05,$
$0.05 \times 10 = 0.5,$
$0.5 \times 10 = 5,$
$5 \times 10 = 50,$
So, Next fraction is $50 \times 10 = 500$
122

Ans: The given pattern,
$0.1,$
$\dfrac{{0.1}}{{10}} = 0.01,$
$\dfrac{{0.01}}{{10}} = 0.001$
$\dfrac{{0.001}}{{10}} = 0.0001$
Next fraction is $\dfrac{{0.0001}}{{10}} = 0.00001$
What is the Error in each of question 123 to 125?
123. A student compared $ - \dfrac{1}{4}$ and ${\mathbf{ - 0}}{\mathbf{.3}}{\mathbf{.}}$ He changed ${\mathbf{ - }}\dfrac{{\mathbf{1}}}{{\mathbf{4}}}$ to the decimal ${\mathbf{ - 0}}{\mathbf{.25}}$ and wrote, "Since ${\mathbf{0}}{\mathbf{.3}}$ is greater than ${\mathbf{0}}{\mathbf{.25, - 0}}{\mathbf{.3}}$ is greater than ${\mathbf{ - 0}}{\mathbf{.25}}$ ". What was the student's error?
Ans: we know that $0.3$ greater than $0.25$
${\text{So}} - 0.3 < - 0.25$
The error is $ - 0.3 > - 0.25$
124. A student multiplied two mixed fractions in the following manner: ${\mathbf{2}}\dfrac{{\mathbf{4}}}{{\mathbf{7}}}{\mathbf{ \times 3}}\dfrac{{\mathbf{1}}}{{\mathbf{4}}}{\mathbf{ = 6}}\dfrac{{\mathbf{1}}}{{\mathbf{7}}}{\mathbf{.}}$ What error the student has done?
Ans: The mixed fraction is
$2\dfrac{4}{7} \times 3\dfrac{1}{4} = \dfrac{{18}}{7} \times \dfrac{{13}}{4}$
$= \dfrac{{9 \times 13}}{{7 \times 2}} = \dfrac{{117}}{{14}} = 8\dfrac{5}{{14}}$
But the given value is ${\mathbf{6}}\dfrac{1}{7}$ which is wrong.
Since $2\dfrac{4}{7} \times 3\dfrac{1}{4} = 6\dfrac{1}{7}$
Therefore, the error is due to the conversion of mixed fractions into an improper fraction.
125. In the pattern $\dfrac{{\mathbf{1}}}{{\mathbf{3}}}{\mathbf{ + }}\dfrac{{\mathbf{1}}}{{\mathbf{4}}}{\mathbf{ + }}\dfrac{{\mathbf{1}}}{{\mathbf{5}}}{\mathbf{ + \ldots \ldots }}$ which fraction makes the sum greater than 1 (first time)? Explain.
Ans: Given pattern, $\dfrac{1}{3} + \dfrac{1}{4} + \dfrac{1}{5} + \ldots $
Case I: $\dfrac{1}{3} + \dfrac{1}{4} + \dfrac{1}{5} = \dfrac{{20 + 15 + 12}}{{60}} = \dfrac{{47}}{{60}}$ is less than \[1\].
Case II: $\dfrac{1}{3} + \dfrac{1}{4} + \dfrac{1}{5} + \dfrac{1}{6} = \dfrac{{20 + 15 + 12 + 10}}{{60}} = \dfrac{{57}}{{60}}$ also less than $1.$
Case III: $\dfrac{1}{3} + \dfrac{1}{4} + \dfrac{1}{5} + \dfrac{1}{6} + \dfrac{1}{7} = \dfrac{{140 + 105 + 84 + 70 + 60}}{{420}} = \dfrac{{459}}{{420}}$ is greater than \[1\].
Hence, $\dfrac{1}{7}$ makes the sum greater than \[1\].
-2\[\begin{bmatrix} 1 & 1\\ -1 & 2\end{bmatrix}\] -1\[\begin{bmatrix} 1 & 1\\ 1 & 2\end{bmatrix}\] +1\[\begin{bmatrix} 1 & 1\\ 1 & -1\end{bmatrix}\]
The NCERT Exemplar solutions for Class 7 Mathematics Chapter 2 contains all the main concepts discussed in the Chapter and helps for better preparation.The NCERT Exemplar for Class 7 Mathematics is the best guide to make sure you know the Chapter well and have a complete review of all the questions that exist in this activity. The Chapter covers a variety of topics such as Appropriate Fractions, Improper Fractions, Mixed Fractions, Decimal Places etc.
The CBSE NCERT Exemplar for Class 7 Mathematics Chapter 2 contains a total of 5 exercises and 125 questions that are all varied and informative. These questions are based on the topics discussed in the Chapter and are represented by theoretical explanations. Exemplary NCERT Exemplar Solutions for Class 7 Mathematics Chapter 2 - Components and Decimals of PDF are available here. Let us now consider some of the topics discussed in this Chapter.
Addition, Subtraction, Division and Repetition of Fractions
Fraction Multiplication By Total Number
Subdivision of Whole Number by Fraction
Reciprocal of Fraction
Fractional Division by Total Number
Multiplication and Division of decimal numbers
Key Topics in NCERT Exemplar Solutions for Class Mathematics 7 Chapter 2 - Fractions and Decimals
Proper and Improper Fractions: In NCERT Exemplar Class 7 of Mathematics Exemplar Chapter 2, you will learn about two basic types of fractions, namely - the right fractions and the wrong fractions. If a fraction is in its entirety then it is called the right fraction and if the fraction is a combined combination of the perfect and suitable fractions, then it is called the wrong fraction. When the wrong part is subdivided it is called a mixed fraction. You will learn about the different functions in this Chapter.
Fractions and Multiplication: The basic concepts and details of duplication of operations are induced in the Chapter. you will learn that to multiply a whole number by the correct subtraction or the wrong fraction, you need to multiply the fraction by a whole number and keep the denominator in its real solution.
Decimals: The basics of Decimals and all the related contexts are discussed in this Chapter. This Chapter will deal with the subtraction of decimal places, the subtraction of integers and mathematical functions and also the conversion of fractions into decimal values in this Chapter.
FAQs on NCERT Exemplar for Class 7 Maths Solutions Chapter 2 Fractions & Decimals
The first task starts with multiple-choice questions when given a partial calculation and you need to select the appropriate option from the four possible answers.
This consists of the photo options and theory-based statements. These questions are test for the students about their analytical skills that are learnt in the Chapter.
Some of the work requires you to fill in the blanks with answers to mathematical questions which have to be applied and considered accurately. The questions require to find the lowest version of a given product.
3. What are Like and Unlike Fractions?
When there is the same denominator then the two fractions are said to be similar. For example, 3/2 and 5/2 are like parts, and we can do addition and subtraction activities. Like:
3/2 + 5/2 = (3 + 5) / 2 = 8/2 = 4
When two fractions have different denominators, they are said to be different from fractions. For example, 3/2 and 4/3 fractions are incorrect and we need to adjust the denominators to make addition and subtraction.
3/2 + 4/3 = (3 × 3) / (2 × 3) + (4 × 2) / (3 × 2)
= (9/6) + (8/6)
= (9 + 8) / 6 = 17/6
4. What is the importance of fractions in daily life?
















