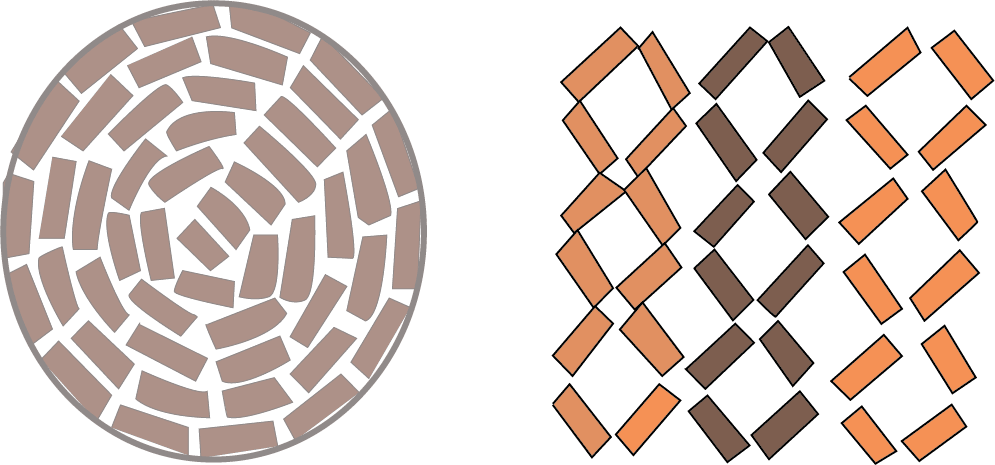Building with Bricks Class 4 Maths Chapter 1 CBSE Notes - 2025-26
Vedantu provides CBSE Class 4 Maths Revision Notes for Chapter 1, Building with Bricks. This chapter introduces students to patterns, shapes, and designs using bricks, making learning both enjoyable and educational. The notes break down key concepts, making it easier for students to understand and apply them.
Table of Content
As aligned with the CBSE Class 4 Maths Syllabus, this chapter focuses on building spatial understanding through real-life examples like brick arrangements. Vedantu’s Class 4 Maths Revision Notes align with the syllabus and help students review important concepts with ease. Download the FREE PDF for a clear and simple way to prepare for exams.
Brick and It Uses
A hard-baked clay block is used for building houses and other structures.
It is used in the construction of walls, arches, floors, etc.
Shape of Brick
Shapes provide an object's boundary.
The shape of the brick is cuboid.
Shape of Brick
Solved Example 1: Can you name any two objects which are cuboid in shape?
Ans: Pencil box, Mobile phones are in the shape of cuboids.
Solved Example 2: Is the shape of the refrigerator a cuboid?
Ans: Yes, the refrigerator is in the shape of a cuboid.
What is a Cuboid?
It is a three-dimensional shape with three dimensions: length, breadth, and height.
Cuboid Dimensions
It has six faces, eight vertices, and twelve edges.
Cuboid faces, edges, and vertices
Real-life examples of cuboids: shoebox, lunch boxes, and mobile phones.
Real-life Cuboid examples
Face of Shape
A solid's face is the name given to each of its flat surfaces.
The face of Brick: A brick is in the shape of a cuboid with 6 rectangular faces.
All the 6 faces of brick are rectangular.
In the below image, the yellow color indicates 6 rectangular faces of brick.
Face of brick
Solved Example 1: How many rectangular faces does a matchbox have?
Ans: A matchbox is in the shape of a cuboid, thus having 6 rectangular faces.
Solved Example 2: In the image given below tick the faces of brick?
Faces of brick
Ans:
Faces of brick
Symmetry(Mirror Half)
Any Object (Shape, letter, or number) that can be divided or folded into two halves along a straight line is said to show Symmetry.
One half of the symmetrical shape is the mirror image of the other.
Symmetrical objects
Solved Example 1: Can you name any two alphabets which possess symmetry?
Ans: Alphabet (A), and (H) possess symmetry.
Solved Example 2: Can you give any two real objects which possess symmetry?
Ans: Leaf, Lungs in our body possess symmetry.
Line of Symmetry
The line that divides a figure into two halves is called the line of symmetry.
For example, We have a tree here, which we may fold into two equal parts.
When a figure is folded in half along its symmetry line, the two parts perfectly match.
Line of symmetry
Brick Patterns
By combining different sizes and shapes of bricks, we may create a wide range of patterns and designs.
Bricks can be used to create wall patterns, tiling patterns, and floor patterns.
Brick patterns
Different Wall Patterns
Using bricks we can create different wall patterns.
Jali patterns and Jharokha patterns are two different types of wall patterns.
Different shapes and sizes of bricks can be used to create different jali wall patterns and jharokha patterns.
In the Jali pattern, some equal spaces are created in the wall to create different symmetrical patterns.
Jali Patterns
In the Jharokha pattern, space is left in the middle of the wall to create an arch design.
Jharokha patterns
Different Floor Patterns
Using bricks we can create different floor patterns.
Circular floor patterns and Symmetrical floor patterns can be created.
Different shapes and sizes of bricks can be used to create different floor patterns.
In the circular pattern, bricks are arranged in circular order whereas in the symmetrical pattern bricks are aligned in some symmetrical design.
Floor patterns
Arch
An arch is a curved construction made of bricks or stones with a curved shape.
For example, Bridge is an arch.
Arch
Cost of Bricks
To calculate the cost of bricks, we need to multiply the number of bricks purchased by the cost of each brick.
Cost of bricks = Number of bricks purchased
cost of each brick.
Solved Example 1: Reena purchased 1000 bricks where each brick costs her ₹12. Find the total cost she paid?
Ans:
Step1: Write the number of bricks purchased = 1000
Step2: Write the cost of each brick= ₹12
Step3: Total cost of bricks = number of bricks purchased х cost of each brick = 1000 х 12 = 1200
So, the Total cost of bricks is ₹1200.
Solved Example 2: Mr. Dixit purchased 5000 bricks where each brick costs her ₹10. Find the total cost she paid?
Ans:
Step1: Write the number of bricks purchased = 5000
Step2: Write the cost of each brick= ₹10
Step3: Total cost of bricks = number of bricks purchased х cost of each brick = 5000 х 10 = 50000
So, the Total cost of bricks is ₹50000.
Solved Example 3: Sam paid ₹1500 per 500 bricks. Find the cost of each brick?
Ans:
Step1: Write the number of bricks purchased = 500
Step2: Write the total cost = ₹1500
Step3: Cost of each brick = Total cost + Total number of bricks purchased = 1500 ፥ 500 = 3
So, the cost of each brick is ₹3.
Practice Questions:
Q1. From the image given below, answer the following questions:
Cuboid
How long is it?
How wide is it?
How high is it?
Q2. Make a drawing of the given cuboidal box to show 3 of its faces.
Cuboidal box
Q3. Draw the line of symmetry for the following figure:
Draw the Line of symmetry
Answers:
Ans 1.
8 cm
2 cm
2 cm
Ans 2.
Drawing of Cuboidal box
Ans 3.
Dotted line is the line of symmetry
5 Important Formulas of Class 4 Maths Chapter 1 Building with Bricks
Importance of Maths Chapter 1 Building with Bricks Class 4 Notes
Revision notes help us quickly understand and remember key concepts before exams.
They save time by focusing on essential information and skipping unnecessary details.
These notes simplify complex topics, making them easier to understand and use.
They provide practical examples that show how theoretical knowledge is used in real-life situations.
They increase confidence by clearly understanding what to expect in exams.
The Class 4 notes of Chapter 1 Building with Bricks cover the fundamental concepts of Building with Bricks.
Tips for Learning the Maths Chapter 1 Building with Bricks Class 4 Notes PDF
Observe brick patterns and designs to better understand shapes and arrangements.
Practice drawing rectangles and squares to understand area and perimeter calculations.
Look for symmetrical patterns in brick designs and practice identifying symmetrical shapes.
Relate the brick designs and calculations to real-life buildings or structures to make learning more practical and fun.
Conclusion
The Building With Bricks Class 4 Revision Notes CBSE Maths Chapter 1 provides a comprehensive and detailed overview of the chapter, introducing students to the concept of 3D objects and the most primitive and common object, a brick. The notes cover important topics such as the six faces of a brick, different brick patterns, and the different ways bricks are used in modern times. The notes also offer practice exercises and questions that help students test their understanding of the chapter and prepare for their exams. These revision notes are an excellent resource for students who want to improve their maths skills and score well in their exams. They are designed by experts according to the CBSE syllabus for Class 4 students and cover all the important topics in the chapter. Overall, the Building With Bricks Class 4 Revision Notes CBSE Maths Chapter 1 are an essential resource for students who want to excel in their mathematics studies.
Related Study Materials for Class 4 Maths Chapter 1
CBSE Class Chapter-wise Class 4 Maths Chapter 1 Revision Notes
Related Study Material Links for Class 4 Maths
FAQs on Building with Bricks Class 4 Maths Chapter 1 CBSE Notes - 2025-26
1. What is the main summary of the CBSE Class 4 Maths chapter, 'Building with Bricks'?
This chapter uses the common brick as a tool to introduce students to fundamental concepts of geometry and arithmetic. A quick revision of this chapter covers the properties of a 3D shape (cuboid), how to visualise objects from different views, the creation of various patterns, and calculations involving large numbers, such as the cost of bricks.
2. What are the key topics to focus on for a quick revision of 'Building with Bricks'?
For an effective revision, you should focus on the following key concepts from the chapter:
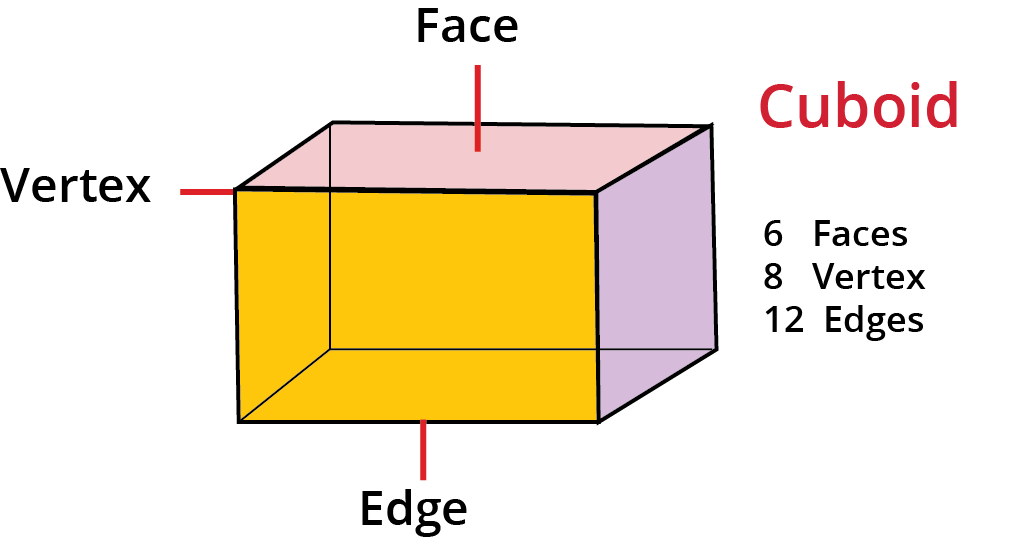
The properties of a brick: its faces (6), edges (12), and corners (8).
Identifying different views of a 3D object (top, front, side).
Recognising and creating different brick patterns, such as floor patterns, 'jaali' (latticework), and 'jharokha' (balcony) designs.
Solving word problems involving large numbers, especially related to the cost and quantity of bricks.
3. How can these revision notes for 'Building with Bricks' help in exam preparation?
These revision notes are designed to help you prepare for exams by summarising the entire chapter into easy-to-digest points. They highlight the most important definitions, formulas, and concepts, ensuring you can quickly recall what you've learned. The notes connect visual concepts like patterns with mathematical calculations, which is crucial for answering application-based questions.
4. What is the difference between a brick's face, edge, and corner?
Understanding these terms is key to describing 3D shapes. A face is the flat surface of the brick. An edge is the straight line where two faces meet. A corner (or vertex) is the point where three edges meet. A standard brick has 6 faces, 12 edges, and 8 corners.
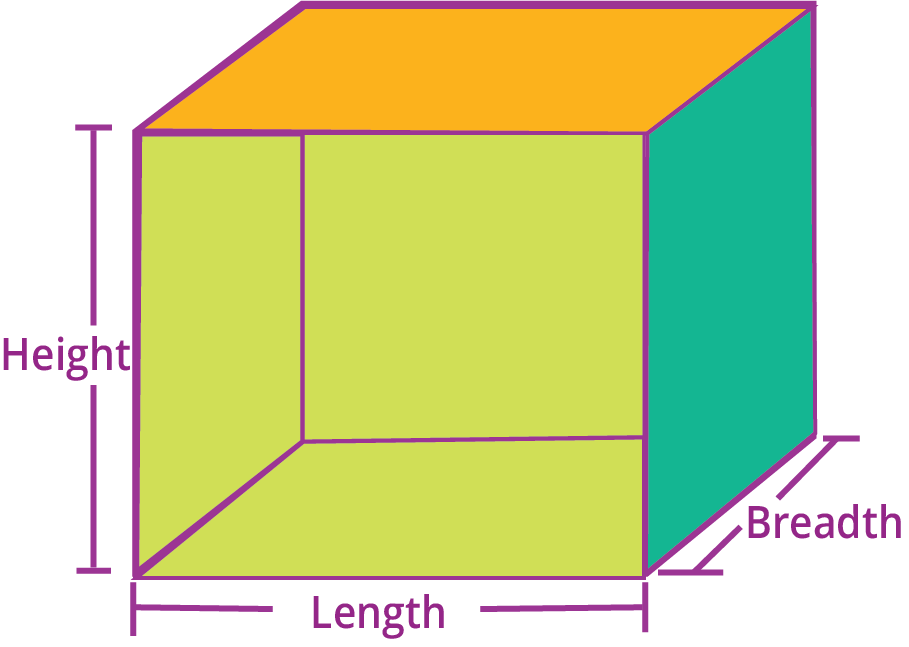
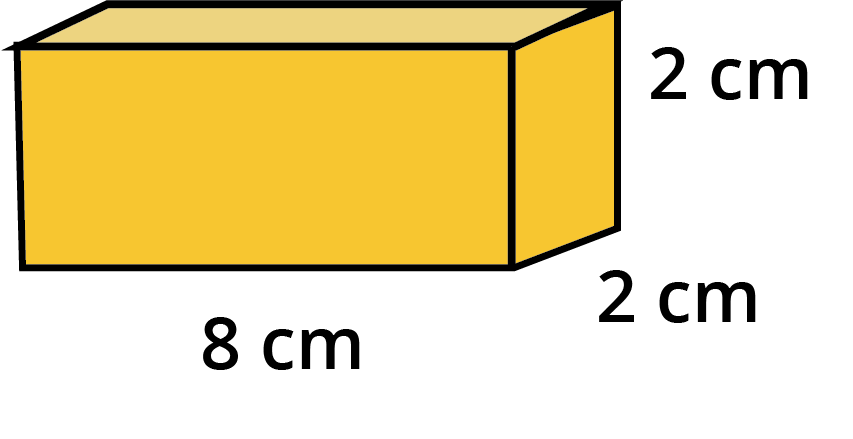
5. Why is a brick shaped like a cuboid and not a cube?
A brick is a cuboid because its length, width, and height are of different measurements. This shape is much more stable for construction than a cube. The different side lengths allow bricks to be laid in interlocking patterns (like a stretcher bond), which distributes weight evenly and creates a much stronger wall. A wall made of cubes would have continuous vertical joints, making it weak.
6. How does this chapter explain different wall patterns like the 'jaali' and 'jharokha'?
The chapter uses these traditional Indian architectural features to show the creative possibilities of brick arrangements. A 'jaali' is a perforated screen or latticework, created by leaving gaps between bricks in a wall. A 'jharokha' is a type of enclosed, overhanging balcony. The notes summarise how these beautiful and functional structures are simply a result of arranging bricks in specific, repeating patterns.
7. What is the difference between a drawing of a brick and a real brick?
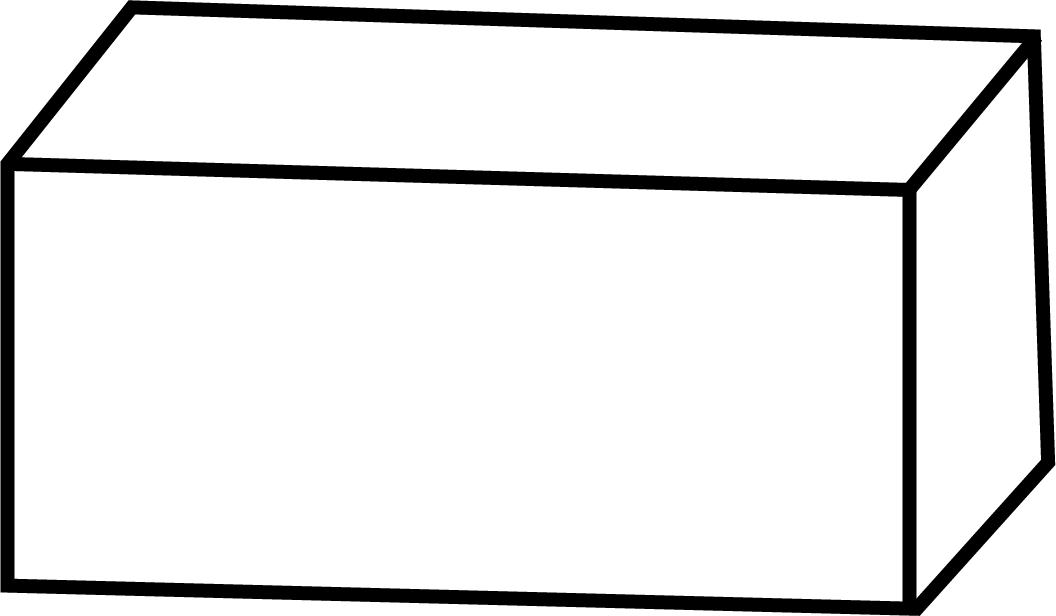
A drawing of a brick is a 2D (two-dimensional) representation on a flat surface like paper. From a single drawing, you can typically see only up to three faces at once. A real brick is a 3D (three-dimensional) object that has length, width, and depth. You can hold it and turn it to see all six of its faces. This chapter helps build the skill of visualising a 3D object from its 2D drawing.
8. How does this chapter introduce calculations with large numbers?
The chapter seamlessly integrates arithmetic with geometry by using real-world scenarios. For example, it presents problems that require calculating the total cost of bricks needed for a wall. This involves multiplying the price of one brick by a large number (like 1000 or 5000), thereby giving practical context to calculations with numbers in the thousands.
9. How does understanding brick patterns help develop problem-solving skills?
Recognising and creating brick patterns is an exercise in spatial reasoning and logical thinking. It trains your brain to identify sequences, predict what comes next, and understand how smaller components fit together to form a larger system. These are foundational skills that are directly applicable to solving more complex mathematical problems in later classes.
10. Besides walls, where else can we apply the concept of patterns learned in this chapter?
The concept of creating complex structures from simple, repeating units is a fundamental idea in many fields. You can see similar patterns in:
The arrangement of floor tiles.
The design of fabrics and carpets (tessellations).
The structure of a honeycomb made by bees.
The pixels on a computer screen forming an image.
It is a core principle in art, design, and nature.
