
What is the slope of \[x=-1\]?
Answer
494.1k+ views
Hint: Slope of a line is a number that describes the both the direction and steepness of the line. \[x=-1\] is a vertical line parallel to y axis and passes through \[\left( -1,0 \right)\]. Since \[x=-1\] is parallel to the y-axis, its slope is equal to the y-axis. We will use slope formula \[m=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}\] where \[m\]is the slope,\[\left( {{x}_{1}},{{y}_{1}} \right)\] and \[\left( {{x}_{2}},{{y}_{2}} \right)\]are two points on the line equation.
Complete step-by-step answer:
From the question we were given the equation of line \[x=-1\] and we were asked to find the slope of the line.
In mathematics, the slope of the line is a number that describes the both the direction and steepness of the line.
Slope is also called the gradient of the line.
Let us try to solve the slope of the line \[x=-1\] by taking two points on the line.
\[A\left( -1,0 \right)\] is the point where the line intersects the x-axis.
\[B\left( -1,2 \right)\]is the point on the line.
\[A\left( -1,0 \right)\] and \[B\left( -1,2 \right)\] are known points on the line \[x=-1\].
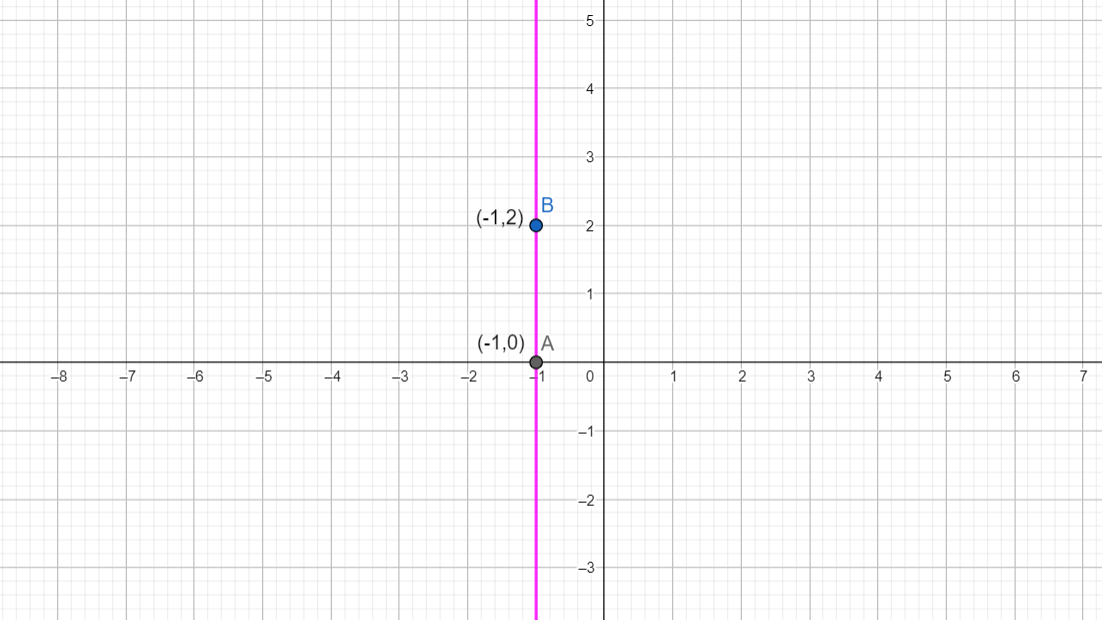
\[\begin{align}
& \Rightarrow \left( {{x}_{2}},{{y}_{2}} \right)=\left( -1,0 \right) \\
& \Rightarrow \left( {{x}_{1}},{{y}_{1}} \right)=\left( -1,2 \right) \\
\end{align}\]
So now We will use slope formula \[m=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}\] to find out the slope.
\[\Rightarrow m=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}\]…………….(1)
Now substitute the corresponding values in equation (1)
\[\Rightarrow m=\dfrac{0-2}{(-1)-(-1)}\]
If we subtract \[-1\]from \[-1\], the resultant will be zero
\[\Rightarrow m=\dfrac{-2}{0}\]
In fraction, denominator cannot be zero. If we ever have zero in the denominator, all we can say that the fraction is undefined.
In \[m=\dfrac{-2}{0}\], we have a denominator as zero. So here \[m\] is undefined.
So, the slope of line \[x=-1\] is undefined.
Note: Students may have the misconception that fraction having denominator zero is infinite but actually it is undefined. Students should be careful while doing calculations because small calculation errors can make getting the slope of line equation \[x=-1\] wrong.
Complete step-by-step answer:
From the question we were given the equation of line \[x=-1\] and we were asked to find the slope of the line.
In mathematics, the slope of the line is a number that describes the both the direction and steepness of the line.
Slope is also called the gradient of the line.
Let us try to solve the slope of the line \[x=-1\] by taking two points on the line.
\[A\left( -1,0 \right)\] is the point where the line intersects the x-axis.
\[B\left( -1,2 \right)\]is the point on the line.
\[A\left( -1,0 \right)\] and \[B\left( -1,2 \right)\] are known points on the line \[x=-1\].

\[\begin{align}
& \Rightarrow \left( {{x}_{2}},{{y}_{2}} \right)=\left( -1,0 \right) \\
& \Rightarrow \left( {{x}_{1}},{{y}_{1}} \right)=\left( -1,2 \right) \\
\end{align}\]
So now We will use slope formula \[m=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}\] to find out the slope.
\[\Rightarrow m=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}\]…………….(1)
Now substitute the corresponding values in equation (1)
\[\Rightarrow m=\dfrac{0-2}{(-1)-(-1)}\]
If we subtract \[-1\]from \[-1\], the resultant will be zero
\[\Rightarrow m=\dfrac{-2}{0}\]
In fraction, denominator cannot be zero. If we ever have zero in the denominator, all we can say that the fraction is undefined.
In \[m=\dfrac{-2}{0}\], we have a denominator as zero. So here \[m\] is undefined.
So, the slope of line \[x=-1\] is undefined.
Note: Students may have the misconception that fraction having denominator zero is infinite but actually it is undefined. Students should be careful while doing calculations because small calculation errors can make getting the slope of line equation \[x=-1\] wrong.
Recently Updated Pages
Explain the double helix structure of DNA with a labeled class 10 biology CBSE

State and prove converse of BPT Basic Proportionality class 10 maths CBSE

Which party gave the slogan Save Democracy in the Lok class 10 social science CBSE

iWhat is Rain Water Harvesting iiWhat are the advantages class 10 social science CBSE

Explain any 5 effects of the Russian Revolution of class 10 social science CBSE

Refractive index of glass with respect to water is class 10 physics CBSE

Trending doubts
Why is there a time difference of about 5 hours between class 10 social science CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

The uses of bleaching powder are A It is used bleaching class 10 chemistry CBSE

What is the minimum age for fighting the election in class 10 social science CBSE

The capital of British India was transferred from Calcutta class 10 social science CBSE

Write any two uses of Plaster of Paris class 10 chemistry CBSE




