
Vibration of magnetometer works on the principle of
A. Torque acting on bar magnet and rotational inertia
B. Force acting on bar magnet and rotational inertia.
C. both force and torque acting on magnet
D. Neither force nor torque.
Answer
534k+ views
Hint: Vibration magnetometer is an instrument used to compare the magnetic moments of two magnets or to determine the horizontal component of the Earth’s magnetic field. When a magnet suspended in a uniform magnetic field (like the one due to earth’s) is displaced from its equilibrium position and it begins to vibrate simply harmonically about the direction of the field.
Formula used:
The time period of vibration magnetometer is given by
\[T=2\pi \sqrt{\dfrac{I}{m{{B}_{H}}}}\], where
$\begin{align}
& m=\text{ magnetic moment of the magnet taken} \\
& {{B}_{H}}=\text{ the horizontal component of earth }\!\!'\!\!\text{ s magnetic field} \\
& I=\text{ the moment of inertia of the magnet about an axis of rotation about its center of mass} \\
& I=\text{Mass of the magnet}\times \dfrac{{{l}^{2}}+{{b}^{2}}}{12} \\
& l\text{ and }b\text{ are the length and bredth of the magnet} \\
\end{align}$
Complete answer:
When a bar magnet is placed in an uniform magnetic field then it will experience a force in the direction of the field due to which the bar magnet will rotate and will try to align with the magnetic field.
The magnet will experience a torque which will rotate the magnet and will try to align with the field due to the rotational inertia the bar magnet will execute simple harmonic motion.
i.e. A vibration magnetometer works on the principle of torque acting on bar magnet and rotational inertia.
So, the correct answer is “Option A”.
Additional Information:
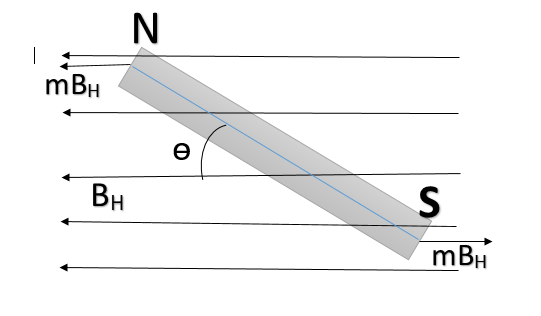
Torque acting on the dipole will be $\tau =m{{B}_{H}}(2l\sin \theta )=2ml{{B}_{H}}\sin \theta =M{{B}_{H}}\sin \theta $
Where
$\begin{align}
& 2l=\text{ length of the bar magnet}\text{.} \\
& \text{M=}2ml=\text{ magnetic dipole moment} \\
\end{align}$
For small $\theta$,$\tau =M{{B}_{H}}\theta $
If $\alpha =\text{ angular acceleration and }I=\text{ moment of inertia}$, then
${{I}_{\alpha }}=M{{B}_{H}}\theta $
So time period of oscillation is
\[T=2\pi \sqrt{\dfrac{I\theta }{{{I}_{\alpha }}}}=2\pi \sqrt{\dfrac{I}{M{{B}_{H}}}}\]
Calculating the horizontal component of earth’s magnetic field:
With the help of a vibration magnetometer we can measure the time period of say $T\text{ and }T'$ of vibration of the same magnet at two given places. Let ${{B}_{H}}\text{ and }{{B}_{H}}'$ are the horizontal component of earth’s magnetic field at these places. Then
\[\begin{align}
& T=2\pi \sqrt{\dfrac{I}{M{{B}_{H}}}}\text{ and }T'=2\pi \sqrt{\dfrac{I}{M{{B}_{H}}}} \\
& \Rightarrow \dfrac{T}{T'}=\sqrt{\dfrac{{{B}_{H}}'}{{{B}_{H}}}} \\
& \Rightarrow \dfrac{{{B}_{H}}}{{{B}_{H}}'}=\dfrac{T{{'}^{2}}}{{{T}^{2}}} \\
\end{align}\]
Note:
Vibration magnetometer works on the principle of torque and rotation in the uniform magnetic field. If the field is non-uniform or the field is very strong the magnet will not oscillate and will stop when aligned with the field. So the vibration magnetometer only works when the field is uniform and not very strong.
Formula used:
The time period of vibration magnetometer is given by
\[T=2\pi \sqrt{\dfrac{I}{m{{B}_{H}}}}\], where
$\begin{align}
& m=\text{ magnetic moment of the magnet taken} \\
& {{B}_{H}}=\text{ the horizontal component of earth }\!\!'\!\!\text{ s magnetic field} \\
& I=\text{ the moment of inertia of the magnet about an axis of rotation about its center of mass} \\
& I=\text{Mass of the magnet}\times \dfrac{{{l}^{2}}+{{b}^{2}}}{12} \\
& l\text{ and }b\text{ are the length and bredth of the magnet} \\
\end{align}$
Complete answer:
When a bar magnet is placed in an uniform magnetic field then it will experience a force in the direction of the field due to which the bar magnet will rotate and will try to align with the magnetic field.
The magnet will experience a torque which will rotate the magnet and will try to align with the field due to the rotational inertia the bar magnet will execute simple harmonic motion.
i.e. A vibration magnetometer works on the principle of torque acting on bar magnet and rotational inertia.
So, the correct answer is “Option A”.
Additional Information:

Torque acting on the dipole will be $\tau =m{{B}_{H}}(2l\sin \theta )=2ml{{B}_{H}}\sin \theta =M{{B}_{H}}\sin \theta $
Where
$\begin{align}
& 2l=\text{ length of the bar magnet}\text{.} \\
& \text{M=}2ml=\text{ magnetic dipole moment} \\
\end{align}$
For small $\theta$,$\tau =M{{B}_{H}}\theta $
If $\alpha =\text{ angular acceleration and }I=\text{ moment of inertia}$, then
${{I}_{\alpha }}=M{{B}_{H}}\theta $
So time period of oscillation is
\[T=2\pi \sqrt{\dfrac{I\theta }{{{I}_{\alpha }}}}=2\pi \sqrt{\dfrac{I}{M{{B}_{H}}}}\]
Calculating the horizontal component of earth’s magnetic field:
With the help of a vibration magnetometer we can measure the time period of say $T\text{ and }T'$ of vibration of the same magnet at two given places. Let ${{B}_{H}}\text{ and }{{B}_{H}}'$ are the horizontal component of earth’s magnetic field at these places. Then
\[\begin{align}
& T=2\pi \sqrt{\dfrac{I}{M{{B}_{H}}}}\text{ and }T'=2\pi \sqrt{\dfrac{I}{M{{B}_{H}}}} \\
& \Rightarrow \dfrac{T}{T'}=\sqrt{\dfrac{{{B}_{H}}'}{{{B}_{H}}}} \\
& \Rightarrow \dfrac{{{B}_{H}}}{{{B}_{H}}'}=\dfrac{T{{'}^{2}}}{{{T}^{2}}} \\
\end{align}\]
Note:
Vibration magnetometer works on the principle of torque and rotation in the uniform magnetic field. If the field is non-uniform or the field is very strong the magnet will not oscillate and will stop when aligned with the field. So the vibration magnetometer only works when the field is uniform and not very strong.
Recently Updated Pages
NCERT Solutions For Class 4 English Marigold (Poem) - Don’t Be Afraid Of The Dark

NCERT Solutions For Class 5 English Marigold (Poem) - Class Discussion

NCERT Solutions For Class 5 English Marigold - Gullivers Travels

NCERT Solutions For Class 5 Hindi Rimjhim - Bagh Aaya Uss Raat

NCERT Solutions For Class 8 Hindi Bharat Ki Khoj - Tanaav

NCERT Solutions For Class 12 Maths - Differential Equations

Trending doubts
Which are the Top 10 Largest Countries of the World?

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Why is the cell called the structural and functional class 12 biology CBSE

a Tabulate the differences in the characteristics of class 12 chemistry CBSE

Who discovered the cell and how class 12 biology CBSE

Draw a labelled sketch of the human eye class 12 physics CBSE




