Question

The wiring of a house has a resistance $6\Omega $. A $100W$, $200V$ bulb is glowing in the bathroom. A geyser of $1000W$, $220V$ is switched on. The drop in potential across the bulb is:
(A) 0
(B) $24V$
(C) $32V$
(D) $12V$

Answer 1

Hint:
We first draw the household circuit where the bulb and the geyser are in parallel. So we calculate the resistance of the bulb and the geyser in the circuit and then can calculate the potential across the bulb in the two cases where the switch is on and off. The difference between these two voltages gives the potential drop.

Formula used: In the solution, we will be using the following formula,
$\Rightarrow P = \dfrac{{{V^2}}}{R}$
where $P$ is the power
 $V$ is the voltage and $R$ is the resistance.
and ${R_{eq}} = \dfrac{{{R_1} \times {R_2}}}{{{R_1} + {R_2}}}$
where ${R_{eq}}$ is the equivalent resistance of a parallel circuit.

Complete step by step answer:
For this question, we draw the following circuit

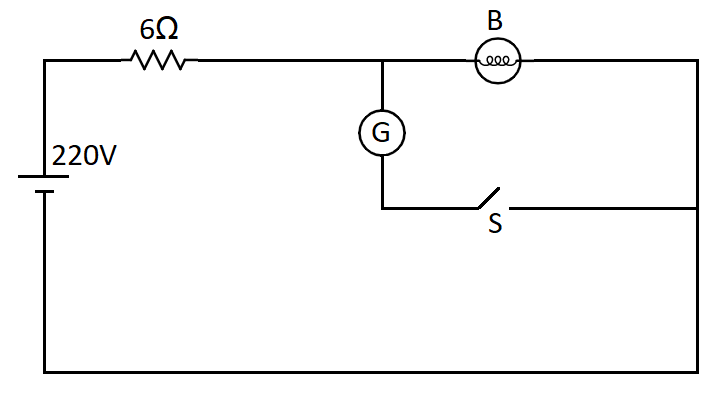
As it is a household circuit so the input voltage is 220V. And the bulb and geyser are connected in parallel as it is a household circuit.
The wiring of the house has a resistance of $6\Omega $ so we can take that resistance as in series with bulb and geyser. So the potential across the bulb will be 220V. So we can find the resistance of the bulb as,
$\Rightarrow P = \dfrac{{{V^2}}}{R}$, it can be written as
$\Rightarrow R = \dfrac{{{V^2}}}{P}$
Now for the bulb, $P = 100W$ and $V = 220V$. Substituting that value we get the resistance of the bulb as,
$\Rightarrow {R_{bulb}} = \dfrac{{220 \times 220}}{{100}}$
So calculating we get,
$\Rightarrow {R_{bulb}} = 484\Omega $
For the geyser, the power is, $P = 1000W$ and $V = 220V$. Substituting these values we get the resistance of the geyser as,
$\Rightarrow {R_{geyser}} = \dfrac{{220 \times 220}}{{1000}}$
So, calculating we get
$\Rightarrow {R_{geyser}} = 48.4\Omega $
Now, for the first case, when the switch S is open, there is no current flowing through the geyser. So the total current in the circuit is,
$\Rightarrow I = \dfrac{V}{{{R_{total}}}}$
Here ${R_{total}}$ is the sum of the resistance of the bulb and the resistance of the wires, given by
$\Rightarrow {R_{total}} = 484 + 6 = 490\Omega $
So the current in the circuit is,
$\Rightarrow I = \dfrac{{220}}{{490}} = 0.449A$
Now the potential across the bulb will be ${V_{bulb}} = I{R_{bulb}}$
Substituting the values we get,
$\Rightarrow {V_{bulb}} = 0.449 \times 484$ that is equal to, ${V_{bulb}} = 217.3V$
For the second case, the switch is on.
Therefore the equivalent resistance will be,
$\Rightarrow {R_{eq}} = \dfrac{{{R_{bulb}} \times {R_{geyser}}}}{{{R_{bulb}} + {R_{geyser}}}}$
Substituting the values we get, ${R_{eq}} = \dfrac{{484 \times 48.4}}{{484 + 48.4}}$
This is equal to, ${R_{eq}} = 44\Omega $
And the total resistance in the circuit is ${R_{total}} = \left( {{R_{eq}} + 6} \right)\Omega $
Substituting the values we get, ${R_{total}} = \left( {44 + 6} \right)\Omega = 50\Omega $
So the current in the circuit in this case is $I = \dfrac{{220}}{{50}} = 4.4A$
Therefore the potential across the bulb will be, ${V_{bulb}} = I \times {R_{eq}}$
Substituting values, the potential is, ${V_{bulb}} = 4.4 \times 44 = 193.6V$
So the difference in the potential across the bulb will be the potential drop across the bulb.
So, ${V_{drop}} = \left( {217.3 - 193.6} \right)V$
So the potential drop across the bulb is ${V_{drop}} = 23.7V$ which is equivalent to 24V.
So the correct answer is option (B); 24V.

Note:
In household circuits, the electrical appliances are connected in parallel because this allows every appliance to be switched on and off independently without affecting any other appliance. Moreover, this makes the potential across all the appliances equal to 220V, so the potential drop across every appliance doesn’t affect the power flow to the other appliance.