
The resultant of two forces $P$$N$ and $3N$ is a force of $7N$. If the direction of $3N$ force were reversed, the resultant would be $\sqrt{19}N$. The value of $P$ is:
$\left( A \right)$ $5N$
$\left( B \right)$$6N$
$\left( C \right)$$3N$
$\left( D \right)$$4N$
Answer
471.6k+ views
Hint: Here we are given that the resultant of two forces $P$ $N$ and $3N$ is a force of $7N$. If the direction of $3N$ force were reversed, the resultant would be $\sqrt{19}N$ and we are asked to find the value of $P$. To find the value of $P$ we will use the concept of laws of vector addition.
Complete step by step solution:
A vector is a quantity which consists of magnitude as well as direction.
Let us see why we need laws of vector addition. We know that force is a vector quantity. If two forces are acting on an object of say mass $m$, then the effect of both of the forces will be what the object will experience in total and since force is a vector quantity we need to add them using laws of vector addition.
The first law is known as the triangular law of vector addition. The triangular law states that: if two vectors represent two sides of a triangle in sequence then the third side in the opposite direction gives us the sum (resultant of two vectors) gives us the sum of the two vectors both in terms of magnitude as well as direction.
Here we are given two vectors $P$$N$and $3N$ whose resultant vector is $7N$. Let us assume the angle between $P$ $N$ and $3N$ is $90{}^\circ $. When the direction of $3N$ vector is reversed the resultant vector is $\sqrt{19}N$. As shown in fig.
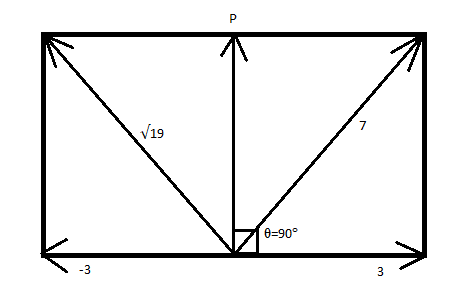
As per triangular law of vector addition,
${{\left( 7 \right)}^{2}}={{P}^{2}}+{{\left( 3 \right)}^{2}}+2(P)(3)\cos \theta ...\left( 1 \right)$
And ${{\left( \sqrt{19} \right)}^{2}}={{P}^{2}}+{{\left( -3 \right)}^{2}}+2\left( P \right)\left( -3 \right)\cos \theta ...\left( 2 \right)$
By adding equations $\left( 1 \right)+\left( 2 \right)$ we get,
$\Rightarrow 49+19=2{{P}^{2}}+18$
0r ${{P}^{2}}=25\Rightarrow P=5N$
Hence, option $\left( A \right)$ is the correct answer.
Note:
One might think that the resultant vector can be obtained by Pythagoras theorem, this thought is incorrect because Pythagoras theorem is not applicable to the resultant of the vectors and is not included in laws of vector addition, one should take care of that.
Complete step by step solution:
A vector is a quantity which consists of magnitude as well as direction.
Let us see why we need laws of vector addition. We know that force is a vector quantity. If two forces are acting on an object of say mass $m$, then the effect of both of the forces will be what the object will experience in total and since force is a vector quantity we need to add them using laws of vector addition.
The first law is known as the triangular law of vector addition. The triangular law states that: if two vectors represent two sides of a triangle in sequence then the third side in the opposite direction gives us the sum (resultant of two vectors) gives us the sum of the two vectors both in terms of magnitude as well as direction.
Here we are given two vectors $P$$N$and $3N$ whose resultant vector is $7N$. Let us assume the angle between $P$ $N$ and $3N$ is $90{}^\circ $. When the direction of $3N$ vector is reversed the resultant vector is $\sqrt{19}N$. As shown in fig.

As per triangular law of vector addition,
${{\left( 7 \right)}^{2}}={{P}^{2}}+{{\left( 3 \right)}^{2}}+2(P)(3)\cos \theta ...\left( 1 \right)$
And ${{\left( \sqrt{19} \right)}^{2}}={{P}^{2}}+{{\left( -3 \right)}^{2}}+2\left( P \right)\left( -3 \right)\cos \theta ...\left( 2 \right)$
By adding equations $\left( 1 \right)+\left( 2 \right)$ we get,
$\Rightarrow 49+19=2{{P}^{2}}+18$
0r ${{P}^{2}}=25\Rightarrow P=5N$
Hence, option $\left( A \right)$ is the correct answer.
Note:
One might think that the resultant vector can be obtained by Pythagoras theorem, this thought is incorrect because Pythagoras theorem is not applicable to the resultant of the vectors and is not included in laws of vector addition, one should take care of that.
Recently Updated Pages
Class 11 Question and Answer - Your Ultimate Solutions Guide

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 Physics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Chemistry: Engaging Questions & Answers for Success

Trending doubts
1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

What is the opposite of entropy class 11 chemistry CBSE

Proton was discovered by A Thomson B Rutherford C Chadwick class 11 chemistry CBSE

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE




