
The phase difference between current and voltage in an AC circuit is $\dfrac{\pi }{4}$ radian. If the frequency of AC is 50 Hz, then the phase difference is equivalent to the time difference :-
A). 0.78s
B). 15.7ms
C). 2.5s
D). 2.5ms
Answer
587.4k+ views
Hint: In an AC circuit, the voltage and the current are treated as vectors. The angle between these two vectors is the phase difference between the voltage and the current. The phase difference is related to the time difference between the voltage and current. For example, a phase difference of $\pi $ radian leads to a time difference of $\dfrac{T}{2}$, where T is the time period. Suppose the current leads the voltage by radian then the voltage reaches its maximum value after time, the current reaches its maximum value.
Formula used: V= $V_{max}$sin($\omega $t +$\phi $)
i = $i_{max}$sin($\omega $t )
Complete step by step answer:
In an AC circuit, the current and the voltage are an oscillating function (sinusoidal functions) of time. For example V= $V_{max}$Sin($\omega $t +$\phi $), where $V_{max}$ is the maximum voltage produced in the circuit, $\omega $ is angular frequency of the circuit, $\phi $ is phase angle and t is time. Similarly, the equation of the current can be written as i= $i_{max}$Sin($\omega $t ). Since these are oscillating functions, they have frequency and time period of oscillations.
In an AC circuit, we consider the voltage and the current as vectors. The angle between these is the phase difference between the voltage and the current in the circuit. The phase difference tells us how much the current is lagging behind or is ahead of the voltage.
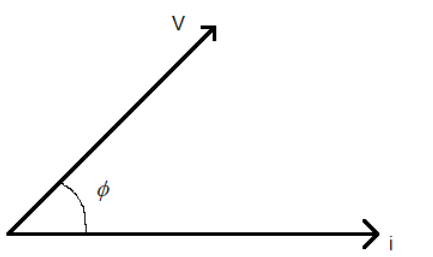
A phase difference of $2\pi $ radians is equal to one complete cycle. $\pi $ radian is equal to half a cycle. Suppose the current is lagging behind the voltage by $\pi $ radians. This means if the voltage reaches its maximum value, after half a cycle, the current will reach its maximum value.
We can relate the phase difference with the time difference between the current and the voltage. We know that a phase difference of $2\pi $ radians is equal to one complete cycle and one complete cycle takes place for time T i.e. the time period.
Therefore, a phase difference of $\dfrac{\pi }{4}$ radians is equal to $\dfrac{1}{8}th$ of a cycle. This means that there is a difference of $\dfrac{1}{8}th$ of a cycle between the current and the voltage. $\dfrac{1}{8}th$ of a cycle is equal to a time difference of $\dfrac{1}{8}T$.
We know that $T=\dfrac{1}{f}$ and f is given as 50 Hz. Therefore, $T=\dfrac{1}{f}=\dfrac{1}{50}s$.
Therefore, the time difference between the voltage and the current is equal to $\dfrac{1}{8}T=\dfrac{1}{8}\times \dfrac{1}{50}=0.0025s=2.5ms$
Hence, the correct option is (D).
Note: It is to be noted that the magnitudes of the vectors of the voltage and the current are the maximum values of the oscillating voltage and oscillating the current in an AC circuit, respectively.
Formula used: V= $V_{max}$sin($\omega $t +$\phi $)
i = $i_{max}$sin($\omega $t )
Complete step by step answer:
In an AC circuit, the current and the voltage are an oscillating function (sinusoidal functions) of time. For example V= $V_{max}$Sin($\omega $t +$\phi $), where $V_{max}$ is the maximum voltage produced in the circuit, $\omega $ is angular frequency of the circuit, $\phi $ is phase angle and t is time. Similarly, the equation of the current can be written as i= $i_{max}$Sin($\omega $t ). Since these are oscillating functions, they have frequency and time period of oscillations.
In an AC circuit, we consider the voltage and the current as vectors. The angle between these is the phase difference between the voltage and the current in the circuit. The phase difference tells us how much the current is lagging behind or is ahead of the voltage.

A phase difference of $2\pi $ radians is equal to one complete cycle. $\pi $ radian is equal to half a cycle. Suppose the current is lagging behind the voltage by $\pi $ radians. This means if the voltage reaches its maximum value, after half a cycle, the current will reach its maximum value.
We can relate the phase difference with the time difference between the current and the voltage. We know that a phase difference of $2\pi $ radians is equal to one complete cycle and one complete cycle takes place for time T i.e. the time period.
Therefore, a phase difference of $\dfrac{\pi }{4}$ radians is equal to $\dfrac{1}{8}th$ of a cycle. This means that there is a difference of $\dfrac{1}{8}th$ of a cycle between the current and the voltage. $\dfrac{1}{8}th$ of a cycle is equal to a time difference of $\dfrac{1}{8}T$.
We know that $T=\dfrac{1}{f}$ and f is given as 50 Hz. Therefore, $T=\dfrac{1}{f}=\dfrac{1}{50}s$.
Therefore, the time difference between the voltage and the current is equal to $\dfrac{1}{8}T=\dfrac{1}{8}\times \dfrac{1}{50}=0.0025s=2.5ms$
Hence, the correct option is (D).
Note: It is to be noted that the magnitudes of the vectors of the voltage and the current are the maximum values of the oscillating voltage and oscillating the current in an AC circuit, respectively.
Recently Updated Pages
A man running at a speed 5 ms is viewed in the side class 12 physics CBSE

State and explain Hardy Weinbergs Principle class 12 biology CBSE

Which of the following statements is wrong a Amnion class 12 biology CBSE

Two Planoconcave lenses 1 and 2 of glass of refractive class 12 physics CBSE

The compound 2 methyl 2 butene on reaction with NaIO4 class 12 chemistry CBSE

Bacterial cell wall is made up of A Cellulose B Hemicellulose class 12 biology CBSE

Trending doubts
What are the major means of transport Explain each class 12 social science CBSE

Which are the Top 10 Largest Countries of the World?

Draw a labelled sketch of the human eye class 12 physics CBSE

State the principle of an ac generator and explain class 12 physics CBSE

Sketch the electric field lines in case of an electric class 12 physics CBSE

Give 10 examples of unisexual and bisexual flowers




