
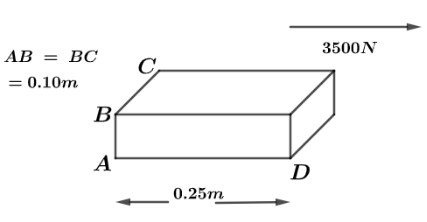
The brick shown in the diagram is glued to the floor. A $3500\,N$ force is applied to the top surface of the brick as shown in the figure. If the brick has shear modulus of $5.4 \times {10^9}\,N{m^{ - 2}}$ , how far to the right does the top face move relative to the stationary bottom face?
A. $5.8 \times {10^{ - 6}}\,m$
B. $2.6 \times {10^{ - 6}}\,m$
C. $1.1 \times {10^{ - 6}}\,m$
D. $6.5 \times {10^{ - 7}}\,m$

Answer
447.9k+ views
Hint: In order to solve this question, we will use the formula of shear modulus which is defined as the ratio of pressure and relative change in length of a material.Shear Modulus of elasticity is one of the measures of mechanical properties of solids. Other elastic moduli are Young’s modulus and bulk modulus.
Formula used:
Shear modulus denoted by,
$S = \dfrac{F}{A} \times \dfrac{x}{{\Delta x}}$
where, $\Delta x$ is the change in length from its initial length $x$.
Complete step by step answer:
Let us first find the area of the cross section which is given by multiplication of sides AD and AB .
$A = 0.25 \times 0.10\,{m^2}$
Given that, force is applied of magnitude $F = 3500\,N$
And original length of sectional area is given as AD, $x = 0.25\,m$
Now, we will use the formula of shear modulus to find the value of $\Delta x$ .
Magnitude of shear modulus is given by $S = 5.4 \times {10^9}N{m^{ - 2}}$
Putting these values in formula $S = \dfrac{F}{A} \times \dfrac{x}{{\Delta x}}$
$\Delta x = \dfrac{{Fx}}{{AS}}$
$\Rightarrow \Delta x = \dfrac{{3500 \times 0.25}}{{5.4 \times {{10}^9} \times 0.25 \times 0.10}}m$
$\therefore \Delta x = 6.5 \times {10^{ - 7}}m$
So, change in length became $\Delta x = 6.5 \times {10^{ - 7}}\,m$
Hence, the correct option is D.
Note:Theoretically, shear modulus can be understood as simply of how much shear stress needed to make a change in shear strain which is the ratio of stress and strain. It deforms the material into a new shape which is due to shear stress applied to its cross sectional areas. Its SI unit is simple as of Pressure given by $N{m^{ - 2}}$ .
Formula used:
Shear modulus denoted by,
$S = \dfrac{F}{A} \times \dfrac{x}{{\Delta x}}$
where, $\Delta x$ is the change in length from its initial length $x$.
Complete step by step answer:
Let us first find the area of the cross section which is given by multiplication of sides AD and AB .
$A = 0.25 \times 0.10\,{m^2}$
Given that, force is applied of magnitude $F = 3500\,N$
And original length of sectional area is given as AD, $x = 0.25\,m$
Now, we will use the formula of shear modulus to find the value of $\Delta x$ .
Magnitude of shear modulus is given by $S = 5.4 \times {10^9}N{m^{ - 2}}$
Putting these values in formula $S = \dfrac{F}{A} \times \dfrac{x}{{\Delta x}}$
$\Delta x = \dfrac{{Fx}}{{AS}}$
$\Rightarrow \Delta x = \dfrac{{3500 \times 0.25}}{{5.4 \times {{10}^9} \times 0.25 \times 0.10}}m$
$\therefore \Delta x = 6.5 \times {10^{ - 7}}m$
So, change in length became $\Delta x = 6.5 \times {10^{ - 7}}\,m$
Hence, the correct option is D.
Note:Theoretically, shear modulus can be understood as simply of how much shear stress needed to make a change in shear strain which is the ratio of stress and strain. It deforms the material into a new shape which is due to shear stress applied to its cross sectional areas. Its SI unit is simple as of Pressure given by $N{m^{ - 2}}$ .
Recently Updated Pages
While covering a distance of 30km Ajeet takes 2 ho-class-11-maths-CBSE

Sanjeevani booti brought about by Lord Hanuman to cure class 11 biology CBSE

A police jeep on patrol duty on a national highway class 11 physics CBSE

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Social Science: Engaging Questions & Answers for Success

Trending doubts
Which one is a true fish A Jellyfish B Starfish C Dogfish class 11 biology CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

How much is 23 kg in pounds class 11 chemistry CBSE

Net gain of ATP in glycolysis a 6 b 2 c 4 d 8 class 11 biology CBSE




