
The band gap between the valence band and the conduction bands in zinc oxide (ZnO) is \[3.2eV\]. Suppose an electron in the conduction band combines with a hole In the valence band and the excess energy is released in the form of electromagnetic radiation. Find the maximum wavelength that can be emitted in this process.
Answer
406.2k+ views
Hint: The formula of the energy in terms of the wavelength has to be used here. The formula consists of the planck's constant, the speed of light in a vacuum, and the wavelength of the light. The energy used here is the maximum. Therefore the wavelength that is calculated from the formula will also be the maximum. The value of the Plank’s constant as well as the speed of light must be known.
Formula Used:
The relationship between the Energy emitted by excited electron \[\left( E \right)\] , planck's constant\[\left( h \right)\] , speed of light in
Vacuum \[\left( c \right)\] , and the wavelength of the emitted light \[\left( \lambda \right)\],
$E = \dfrac{{hc}}{\lambda }$
Complete step by step answer:
the maximum energy emitted by the excited electron
$E = \dfrac{{hc}}{\lambda }$
\[\left( \lambda \right)\]is the maximum wavelength.
planck's constant \[\left( h \right)\]
Numerically, \[h = 6.62 \times {10^{ - 34}}{m^2}kg/s\]
\[\left( c \right)\] is the speed of light in a vacuum, \[c = 3 \times {10^8}m/s\]
In the given question we are given:-
\[E = 3.2eV\]
The emitted energy can be rewritten in terms of volts
\[E = 3.2 \times 1.6{\text{ }}x{\text{ }}{10^{ - 19}} = 5.12{\text{ }}x{\text{ }}{10^{ - 19}}V\]
We can rewrite the equation as
$\lambda = \dfrac{{hc}}{E}$
We can solve the substituted equation as
\[\lambda = \dfrac{{\left( {6.62 \times {{10}^{ - 34}} \times 3 \times {{10}^8}} \right)}}{{5.12 \times {{10}^{ - 19}}}}m\]
so,
\[\lambda = \dfrac{{\left( {19.86 \times {{10}^{ - 24}}} \right)}}{{5.12 \times {{10}^{ - 19}}}}m\]
The calculated value of the emitted energy’s wavelength
\[\lambda = 3.88 \times {10^{ - 7}}m\]
The maximum wavelength that can be emitted in this process equals \[3.88 \times {10^{ - 7}}m\]
Note:
In semiconductors ( group- \[14\] elements), acc. to the band theory $3$ types of bands are found in them-:
Valence band- In this band electrons can be found at room temperature. But the electrons in this band can’t participate in the flow of current if an external voltage is applied to it.
Conduction band- In this band electrons are rarely found at room temperature. But the electrons present in these bands can actively participate in the flow of current in presence of applied external voltage.
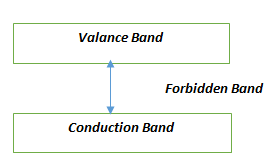
Forbidden band/Gap- It is the energy difference between the conduction band and valence band. Generally, it is measured in electron volts \[\left( {eV} \right)\] .
Formula Used:
The relationship between the Energy emitted by excited electron \[\left( E \right)\] , planck's constant\[\left( h \right)\] , speed of light in
Vacuum \[\left( c \right)\] , and the wavelength of the emitted light \[\left( \lambda \right)\],
$E = \dfrac{{hc}}{\lambda }$
Complete step by step answer:
the maximum energy emitted by the excited electron
$E = \dfrac{{hc}}{\lambda }$
\[\left( \lambda \right)\]is the maximum wavelength.
planck's constant \[\left( h \right)\]
Numerically, \[h = 6.62 \times {10^{ - 34}}{m^2}kg/s\]
\[\left( c \right)\] is the speed of light in a vacuum, \[c = 3 \times {10^8}m/s\]
In the given question we are given:-
\[E = 3.2eV\]
The emitted energy can be rewritten in terms of volts
\[E = 3.2 \times 1.6{\text{ }}x{\text{ }}{10^{ - 19}} = 5.12{\text{ }}x{\text{ }}{10^{ - 19}}V\]
We can rewrite the equation as
$\lambda = \dfrac{{hc}}{E}$
We can solve the substituted equation as
\[\lambda = \dfrac{{\left( {6.62 \times {{10}^{ - 34}} \times 3 \times {{10}^8}} \right)}}{{5.12 \times {{10}^{ - 19}}}}m\]
so,
\[\lambda = \dfrac{{\left( {19.86 \times {{10}^{ - 24}}} \right)}}{{5.12 \times {{10}^{ - 19}}}}m\]
The calculated value of the emitted energy’s wavelength
\[\lambda = 3.88 \times {10^{ - 7}}m\]
The maximum wavelength that can be emitted in this process equals \[3.88 \times {10^{ - 7}}m\]
Note:
In semiconductors ( group- \[14\] elements), acc. to the band theory $3$ types of bands are found in them-:
Valence band- In this band electrons can be found at room temperature. But the electrons in this band can’t participate in the flow of current if an external voltage is applied to it.
Conduction band- In this band electrons are rarely found at room temperature. But the electrons present in these bands can actively participate in the flow of current in presence of applied external voltage.

Forbidden band/Gap- It is the energy difference between the conduction band and valence band. Generally, it is measured in electron volts \[\left( {eV} \right)\] .
Recently Updated Pages
Master Class 12 Biology: Engaging Questions & Answers for Success

Master Class 12 Physics: Engaging Questions & Answers for Success

Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Business Studies: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Trending doubts
Which are the Top 10 Largest Countries of the World?

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Why is the cell called the structural and functional class 12 biology CBSE

a Tabulate the differences in the characteristics of class 12 chemistry CBSE

Who discovered the cell and how class 12 biology CBSE

Draw a labelled sketch of the human eye class 12 physics CBSE




