
State and derive law of conservation of momentum.
Answer
564.6k+ views
Hint: We need to understand the fundamental principles in the mechanics to understand the property of momentum and the laws which govern the linear momentum. The conservation law of linear momentum can be derived from Newton’s laws of motion.
Complete answer:
The linear momentum is defined as the combined effect of mass and velocity of an object experienced by another object which interacts with the former. The linear momentum is the product of the mass of a body and the velocity at which it travels. It is mathematically given as –
\[p=mv\]
A body which moves with a velocity ‘v’ can cause an impact on another object which collides with this body.
The conservation of linear momentum states that the linear momentum possessed by a system before and after collision will remain a constant, given that no external forces act in the system, i.e., there is no chance of acceleration.
Let us consider two particles moving against each other with forces \[{{F}_{1}}\text{ and }{{F}_{2}}\].
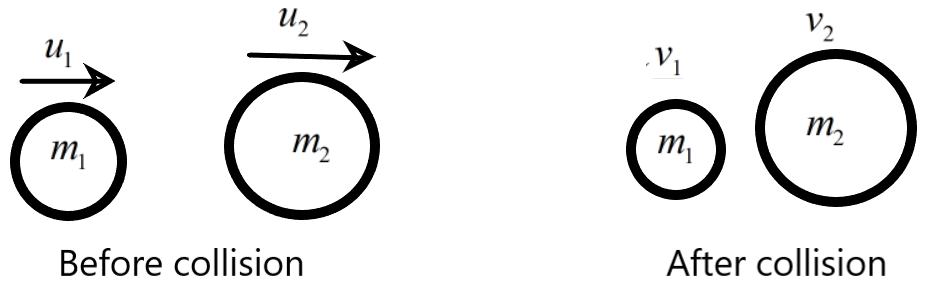
According to Newton's third law of motion, we know that every action has an equal and opposite reaction. So, once the two objects each of mass \[{{m}_{1}}\text{ and }{{m}_{2}}\] collide with each other, the forces acting will be equal and opposite. So, we can derive the momentum (let ‘v’ represent the final velocity of each mass after collision and ‘u’ represent the initial velocity before collision) as –
\[\begin{align}
& {{F}_{1}}={{m}_{1}}{{a}_{1}} \\
& \Rightarrow {{F}_{1}}={{m}_{1}}(\dfrac{{{v}_{1}}-{{u}_{1}}}{t}) \\
& \text{and,} \\
& {{F}_{2}}={{m}_{2}}{{a}_{2}} \\
& \Rightarrow {{F}_{2}}={{m}_{2}}(\dfrac{{{v}_{2}}-{{u}_{2}}}{t}) \\
\end{align}\]
\[\begin{align}
& \text{Now,} \\
& {{F}_{1}}=-{{F}_{2}} \\
& \Rightarrow {{m}_{1}}(\dfrac{{{v}_{1}}-{{u}_{1}}}{t})={{m}_{2}}(\dfrac{{{v}_{2}}-{{u}_{2}}}{t}) \\
& \Rightarrow {{m}_{1}}{{v}_{1}}-{{m}_{1}}{{u}_{1}}={{m}_{2}}{{v}_{2}}-{{m}_{2}}{{u}_{2}} \\
& \therefore {{m}_{1}}{{u}_{1}}+{{m}_{2}}{{u}_{2}}={{m}_{1}}{{v}_{1}}+{{m}_{2}}{{v}_{2}} \\
\end{align}\]
We understand that the sum of the initial momenta of the two bodies is equal to the sum of the final momenta. Thus, the law of conservation of momentum is proved.
This is the required solution.
Note:
The conservation of linear momentum is valid only when there is no external net force acting on the masses involved in the system. We can apply the law of conservation of energy in such cases where there is an external force in the system.
Complete answer:
The linear momentum is defined as the combined effect of mass and velocity of an object experienced by another object which interacts with the former. The linear momentum is the product of the mass of a body and the velocity at which it travels. It is mathematically given as –
\[p=mv\]
A body which moves with a velocity ‘v’ can cause an impact on another object which collides with this body.
The conservation of linear momentum states that the linear momentum possessed by a system before and after collision will remain a constant, given that no external forces act in the system, i.e., there is no chance of acceleration.
Let us consider two particles moving against each other with forces \[{{F}_{1}}\text{ and }{{F}_{2}}\].

According to Newton's third law of motion, we know that every action has an equal and opposite reaction. So, once the two objects each of mass \[{{m}_{1}}\text{ and }{{m}_{2}}\] collide with each other, the forces acting will be equal and opposite. So, we can derive the momentum (let ‘v’ represent the final velocity of each mass after collision and ‘u’ represent the initial velocity before collision) as –
\[\begin{align}
& {{F}_{1}}={{m}_{1}}{{a}_{1}} \\
& \Rightarrow {{F}_{1}}={{m}_{1}}(\dfrac{{{v}_{1}}-{{u}_{1}}}{t}) \\
& \text{and,} \\
& {{F}_{2}}={{m}_{2}}{{a}_{2}} \\
& \Rightarrow {{F}_{2}}={{m}_{2}}(\dfrac{{{v}_{2}}-{{u}_{2}}}{t}) \\
\end{align}\]
\[\begin{align}
& \text{Now,} \\
& {{F}_{1}}=-{{F}_{2}} \\
& \Rightarrow {{m}_{1}}(\dfrac{{{v}_{1}}-{{u}_{1}}}{t})={{m}_{2}}(\dfrac{{{v}_{2}}-{{u}_{2}}}{t}) \\
& \Rightarrow {{m}_{1}}{{v}_{1}}-{{m}_{1}}{{u}_{1}}={{m}_{2}}{{v}_{2}}-{{m}_{2}}{{u}_{2}} \\
& \therefore {{m}_{1}}{{u}_{1}}+{{m}_{2}}{{u}_{2}}={{m}_{1}}{{v}_{1}}+{{m}_{2}}{{v}_{2}} \\
\end{align}\]
We understand that the sum of the initial momenta of the two bodies is equal to the sum of the final momenta. Thus, the law of conservation of momentum is proved.
This is the required solution.
Note:
The conservation of linear momentum is valid only when there is no external net force acting on the masses involved in the system. We can apply the law of conservation of energy in such cases where there is an external force in the system.
Recently Updated Pages
Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Chemistry: Engaging Questions & Answers for Success

Which cell organelles are present in white blood C class 11 biology CBSE

What is the molecular geometry of BrF4 A square planar class 11 chemistry CBSE

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Explain zero factorial class 11 maths CBSE

State the laws of reflection of light

Difference Between Prokaryotic Cells and Eukaryotic Cells

Show that total energy of a freely falling body remains class 11 physics CBSE




